Механические колебания

Дата: 2025-05-25; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Основные формулы

Всякое колебательное движение, в том числе и гармоническое, характеризуется амплитудой 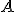, периодом колебаний 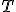, частотой 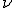, циклической (круговой) частотой 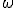и фазой колебаний .

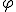Амплитудой 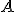называют наибольшее значение колеблющейся величины.
Число полных колебаний в единицу времени называют частотой:
.
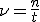Циклическая (круговая) частота - это число полных колебаний в течении 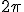с:
.
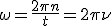Периодом называю время, в течении которого совершается одно полное колебание:
.

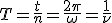Смещение, скорость и ускорение при гармоническом колебании определяются уравнениями

,
,
.

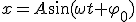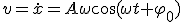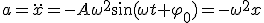Здесь 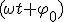- фаза колебаний, а 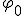- начальная фаза.

Сила, действующая на тело при свободном гармоническом колебании (квазиупругая сила), всегда пропорциональна смещению и направлена в сторону, противоположную смещению:

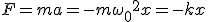
где 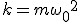- коэффициент квазиупругой силы, измеряемый силой, вызывающей смещение 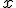, равное единице.

При отсутствии сопротивления среды циклическая частота 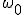свободных гармонических колебаний, называемых собственной циклической частотой и период 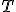равны:

,

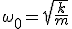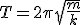
Период колебания математического маятника длиной 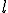равен

.

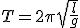Период колебаний физического маятника

,

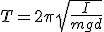где 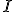- момент инерции маятника относительно оси качаний, 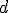- расстояние от оси его до центра тяжести.

Полная энергия тела, совершающего гармонические колебания, постоянна и равна

.

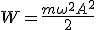Уравнение смещения в затухающих колебаниях при наличии силы сопротивления 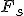пропорциональной скорости ( 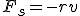, где - коэффициент сопротивления) имеет вид:

.

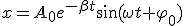Здесь 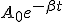- убывающая по времени амплитуда смещения; 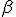- коэффициент затухания; 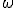- циклическая частота; 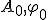- начальные амплитуда и фаза, определяются из начальных условий.

Величины 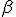и 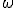выражаются через параметры системы 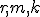формулами:

,

.

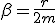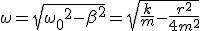Логарифмический декремент затухания

,

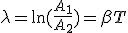где 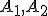- амплитуды двух последовательных колебаний.

Амплитуда вынужденных колебаний

,

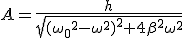где 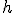- есть отношение амплитуды вынуждающей силы к массе тела; 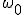- собственная циклическая частота; 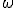- циклическая частота вынуждающей силы.

Резонансная циклическая частота равна

.

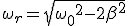Электромагнитные волны:

1

Уравнение Бернулли — для стабильно текущего потока (газа или жидкости) сумма кинетической и потенциальной энергии, давления на единицу объема является постоянной в любой точке этого потока.

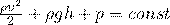
Первое и второе слагаемое в Законе Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. А третье слагаемое в нашей формула является работой сил давления и не запасает какую-либо энергию. Из этого можно сделать вывод, что размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости или газа.

Постоянная в правой части уравнения Бернулли называется полным давлением и зависит в общих случаях, только от линии потока.

Если у вас горизонтальная труба, то Уравнение Бернулли принимает некий другой вид. Так как h=0, то потенциальная энергия будет равняться нулю, и тогда получится :

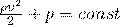
Из Уравнения Бернулли можно сделать один важный вывод. При уменьшении сечения потока возрастает скорость движения газа или жидкости (возрастает динамическое давление 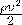), но в этот же момент уменьшает статическое давление следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление 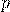падает.

Давайте узнаем, как же летают самолеты. Даниил Бернулли объединил законы механики Ньютона с законом сохранения энергии и условием неразрывности жидкости, и смог вывести уравнение (Уравнение Бернулли), согласно которому давление со стороны текучей среды (жидкость или газ) падает с увеличением скорости потока этой среды. В случае с самолетом воздух обтекает крыло самолета снизу медленне, чем сверху. И благодаря этому эффекту обратной зависимости давления от скорости давление воздуха снизу, направленное вверх, оказывается больше давления сверху, напрвленного вниз. В результате, по мере набора самолетом скорости, возрастает направленная вверх разность давлений, и на крылья самолета действует нарастающая по мере разгона подъемная сила. Как только она начинает превышать силу гравитационного притяжения самолета к земле, самолет в буквальном смысле взмывает в небо. Эта же сила удерживает самолет в горизонтальном полете: на крейсерской скорости и высоте подъемная сила уравновешивает силу тяжести.

2

точки зрения механики, жидкостью называется вещество, в котором в равновесии отсутствуют касательные напряжения. Если движение жидкости не содержит резких градиентов скорости, то касательными напряжениями и вызываемым ими трением можно пренебречь и при описании течения. Если вдобавок малы градиенты температуры, то можно пренебречь и теплопроводностью, что и составляет приближение идеальной жидкости. В идеальной жидкости, таким образом, рассматриваются только нормальные напряжения, которые описываются давлением. В изотропной жидкости, давление одинаково по всем направлениям и описывается скалярной функцией

Идеа́льная жи́дкость — в гидродинамике — воображаемая несжимаемая жидкость, в которой отсутствуют вязкость и теплопроводность. Так как в ней отсутствует внутреннее трение, то нет касательных напряжений между двумя соседними слоями жидкости.

Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. В частности, такая идеализация допустима во многих случаях течения, рассматриваемых гидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Математическое описание течений идеальных жидкостей позволяет найти теоретическое решение ряда задач о движении жидкостей и газов в каналах различной формы, при истечении струй и при обтекании тел.

Вязкость - свойство жидкости оказывать сопротивление относительному движению (сдвигу) частиц жидкости. Это свойство обусловлено возникновением в движущейся жидкости сил внутреннего трения, ибо они проявляются только при ее движении благодаря наличию сил сцепления между ее молекулами. Характеристиками вязкости являются: динамический коэффициент вязкости μ икинематический коэффициент вязкости ν.

Единицей динамического коэффициента вязкости в системе СГС является пуаз (П): 1 П=1 дина·с/см²=1 г/(см·с). Сотая доля пуаза носит название сантипуаз (сП): 1 сП=0,01П. В системе МКГСС единицей динамического коэффициента вязкости является кгс·с/м²; в системе СИ - Па·с. Связь между единицами следующая: 1 П=0,010193 кгс·с/м²=0,1 Па·с; 1 кгс·с/м²=98,1 П=9,81 Па·с.

Кинематический коэффициент вязкости

ν=μ/ρ,

Единицей кинематического коэффициента вязкости в системе СГС является стокc (Ст), или 1 см²/с, а также сантистокс (сСт): 1 сСт=0,01 Ст. В системах МКГСС и СИ единицей кинематического коэффициента вязкости является м²/с: 1 м²/с=10⁴Ст.

Вязкость жидкости с повышением температуры уменьшается. Влияние температуры на динамический коэффициент вязкости жидкостей оценивается формулой μ = μ₀·e^­a(t-t₀⁾, где μ = μ₀ - значения динамического коэффициента вязкости соответственно при температуре t и t₀ градусов; а - показатель степени, зависящий от рода жидкости; для масел, например, значения его изменяются в пределах 0,025—0,035.

Для смазочных масел и жидкостей, применяемых в машинах и гидросистемах, предложена формула, связывающая кинематический коэффициент вязкости и температуру:

ν_t=ν50·(50/t₀)ⁿ,

где ν_t - кинематический коэффициент вязкости при температуре t⁰;
ν50 - кинематический коэффициент вязкости при температуре 50 ⁰С;
t - температура, при которой требуется определить вязкость, ⁰С;
n - показатель степени, изменяющийся в пределах от 1,3 до 3,5 и более в зависимости от значенияν50.

С достаточной точностью n может определяться выражением n=lgν50+2,7. Значения n в зависимости от исходной вязкости ν при 50 ⁰С приведены далее в таблице

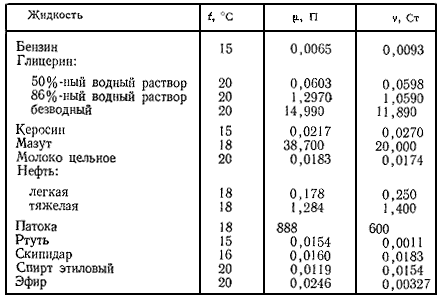
Значения динамического и кинематического коэффициентов вязкости некоторых жидкостей приведены далее в таблице

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.

Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Справедлив общий закон внутреннего трения — закон Ньютона:

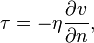
Коэффициент вязкости 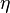(коэффициент динамической вязкости, динамическая вязкость) может быть получен на основе соображений о движениях молекул. Очевидно, что 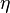будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде:

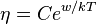
Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества 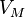. Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение

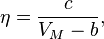
где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.

Динамическая вязкость жидкостей уменьшается с увеличением температуры, и растёт с увеличением давления.

Значение коэффициентов кинематической и динамической вязкости пресной воды