Четыре замечательные точки треугольника. Геометрия 8
 Задачи.
Задачи.
№ 674
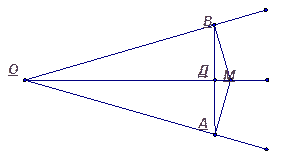
Дано: 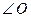 , ОМ – биссектриса
, ОМ – биссектриса
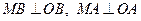
Док-ть: 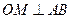
Док – во:
1. ∆ ОМВ = ∆ ОМА ( по гипотенузе и острому углу), то
ОВ = ОА, сл-но ∆ АОВ - равнобедренный, тогда
Биссектриса ОД – является медианой и высотой, то 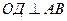 .
.
 2.
2. 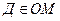 , то
, то 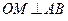 , ч.т.д.
, ч.т.д.
№ 676
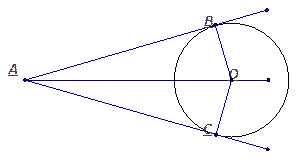
Дано: 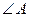 , Окр.(О, 5),
, Окр.(О, 5), 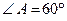
Найти: ОА
Решение:
1. ∆ АОВ = ∆ АОС ( по гипотенузе и катету),
тогда 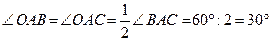 .
.
2. ∆ АОВ, 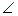 В = 90º, sin
В = 90º, sin 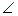 АОВ = ВО: ОА,
АОВ = ВО: ОА,
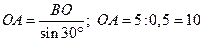 (см).
(см).
ОТВЕТ: ОА = 10 см.
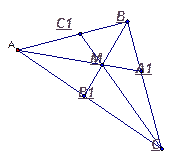 |
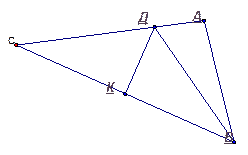
№ 678(а)
Дано: ∆ АВС, 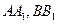 - биссектрисы
- биссектрисы
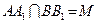 ,
, 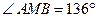
Найти: 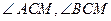
Решение:
1. Так как 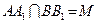 , то третья биссектриса
, то третья биссектриса 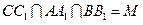 ,
,
тогда 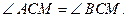
2. ∆ АВМ : 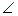 1 +
1 + 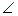 3= 180º - 136º = 44º
3= 180º - 136º = 44º
3. ∆ АВС: 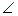 А +
А + 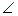 В = (
В = ( 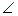 1 +
1 + 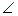 2) + (
2) + ( 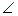 3 +
3 + 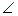 4) = 2(
4) = 2( 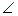 1 +
1 + 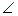 3) = 2 · 44º= 88º
3) = 2 · 44º= 88º
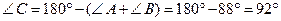
4. 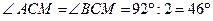
ОТВЕТ: 46 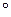 .
.
 |
№ 679(а)
Дано: ∆ АВС, КД – серединный перпендикуляр
ДВ = 5см, АС = 8,5см
Найти: АС, СД
Решение:
1. Т.к. ДК - серединный перпендикуляр, то СД = ВД = 5(см)
2. АД = АС – ДС = 8,5 – 5 = 3,5 (см).
ОТВЕТ: 5см, 3,5см.
Задачи по теме « Окружность». Геометрия 8
1 ВАРИАНТ
1. В треугольник вписана окружность так, что три из шести получившихся отрезков
касательных равны 2см, 4см, 6см. Определите вид треугольника.
2. Точки А и В делят окружность с центром О на дуги АМВ и АСВ так, что дуга АСВ
на 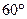 меньше дуги АМВ. АМ – диаметр окружности. Найдите углы АМВ, АВМ, АСВ.
меньше дуги АМВ. АМ – диаметр окружности. Найдите углы АМВ, АВМ, АСВ.
3. Хорды АВ и СД пересекаются в точке Е так, что АЕ = 3см,ВЕ = 36см, СЕ : ДЕ = 3 : 4.
Найдите СД и наименьшее значение радиуса этой окружности.
4. В равнобедренном треугольнике боковая сторона равна 10см, а биссектриса,
проведенная к основанию 8см. Найдите радиус окружности, вписанной в этот
треугольник, и радиус окружности, описанной около этого треугольника.
2 ВАРИАНТ
1. В треугольник вписана окружность радиусом 2см так, что один из получившихся
отрезков касательных равен 4см. Найдите стороны треугольника, если его периметр
равен 24см.
2. Точки Е и Н делят окружность с центром О на дуги ЕАН и ЕКН так, что дуга ЕКН на
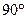 меньше дуги ЕАН, ЕА – диаметр окружности. Найдите углы ЕКА, ЕАН, ЕКН.
меньше дуги ЕАН, ЕА – диаметр окружности. Найдите углы ЕКА, ЕАН, ЕКН.
3. Хорды МН и РК пересекаются в точке А так, что МА = 3см, АН = 16см, РК : КА = 1 : 3.
Найдите РК и наименьшее значение радиуса этой окружности.
4. В равнобедренном треугольнике основание равно 10см, а высота, проведенная к ней,
равна 12см. Найдите радиус окружности, вписанной в этот треугольник, и радиус
окружности, описанной около этого треугольника.
ОТВЕТЫ.
1 ВАРИАНТ 2 ВАРИАНТ
1. 6см, 8см, 10см, прямоугольный 1. 6см, 8см, 10см. 2.
2. 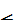 АМВ =75
АМВ =75  ,
,  АВМ =90
АВМ =90  ,
,  АСВ =105
АСВ =105  . 2.
. 2. 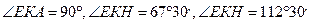
3. 19,5см 3. 9,5см
 4. r = 3 см, R = 6,25см. 4. r = 3 см, R = 7см
4. r = 3 см, R = 6,25см. 4. r = 3 см, R = 7см
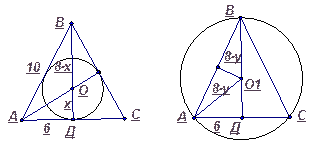
рис. 1 ОВ = 8 – х , ОД = х
рис. 2 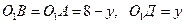
Рис. 1 Рис. 2








