Окружность. Задачи. Геометрия 8
1. Радиус окружности 5см. Найдите расстояние от центра окружности до прямой, содержащей хорду, равную 8см.
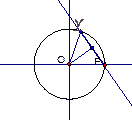
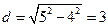 (см).
(см).
2. Найдите расстояние от точки А до ближайшей к ней точки окружности с центром О радиуса r, если : а) ОА = 12см, r = 8см; б) ОА = 6см, r = 8см.
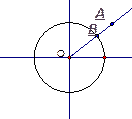
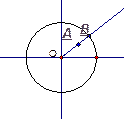
АВ = ОА - r, АВ = r – ОА,
АВ = 12 – 8 = 4(см) АВ = 8 – 6 = 2(см)
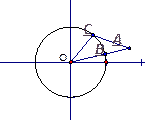 3. Докажите, что АВ ‹ АС, используя неравенство треугольника.
3. Докажите, что АВ ‹ АС, используя неравенство треугольника.
Имеем ОА‹ ОС + АС
ОВ + АВ ‹ ОС + АС, т.к. ОВ = ОС = r,
То АВ ‹ АС.
Изложить материал в виде небольшой лекции.
Итоги урока.
 1.
1. 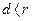 , прямая А – секущая.
, прямая А – секущая.
2. 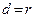 , прямая а имеет с окружностью
, прямая а имеет с окружностью
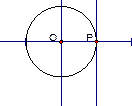 одну общую точку.
одну общую точку.
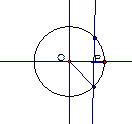
3. 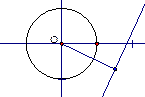
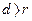 , прямая а не имеет общих точек
, прямая а не имеет общих точек
с окружностью.
Касательная к окружности. Геометрия 8
Задачи (1).
1. Через концы диаметра АВ окружности проведены две касательные к ней. Третья касательная пересекает первые две в точках С и Д. Докажите, что квадрат радиуса этой окружности равен произведению отрезков СА и ВД.
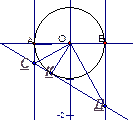
Решение
Очевидно, что ∆ СОД - прямоугольный.
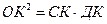 , но АС = СК, ВД = КД
, но АС = СК, ВД = КД
(св-во 2-х касательных, проведенных из одной точки к окружности)
Поэтому 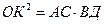 .
.
Ч.т.д.
2. Из точки, кратчайшее расстояние которой до окружности равно 25мм, проведена к окружности касательная. Отрезок этой касательной между данной точкой и точкой касания равен 35мм. Найти длину диаметра окружности.
Решение.
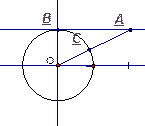 ∆ АОВ,
∆ АОВ,  В = 90º. По теореме Пифагора:
В = 90º. По теореме Пифагора:
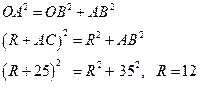
Ответ: Длина диаметра равна 24 мм.
3. Из точки, наибольшее расстояние которой до окружности 50мм, проведена к окружности касательная. Отрезок этой касательной между точкой касания и данной точкой равен 40мм. Найти длину диаметра окружности.
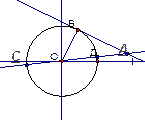
Решение.
∆ АОВ,  В = 90º. По теореме Пифагора:
В = 90º. По теореме Пифагора:
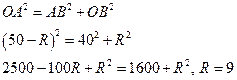
Ответ: Длина диаметра равна 18 мм.
Касательная к окружности. Геометрия 8
 Задачи (2).
Задачи (2).
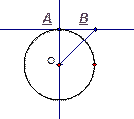
1. Дано: R = 5, АВ – касательная.
Найти: ОВ
Рис. 1
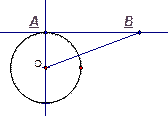 |
2. Дано: АВ – касательная,
АВ = 12, ОВ = 13
Найти: R окружности.
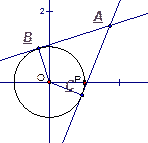
Рис. 2
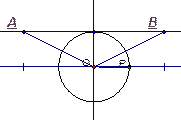
3. Дано: АВ, ВС – касательные,
АО = 4, ОВ = 2
Найти: 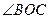 .
.
Рис. 3
4. Дано: АВ – касательная,
АО = ОВ, R = 6, АВ = 16
Найти: АО.
Рис. 4
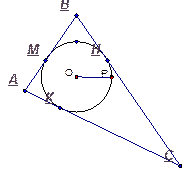 |
5. Дано: М, Н, К - точки касания
МВ = 4, АК = 5, НС = 8.
Найти: 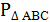
Рис. 5
Самостоятельная работа.
1 ВАРИАНТ
1. Прямая КЕ касается окружности с центром в точке О, К – точка касания. Найдите ОЕ, если КЕ = 8см, а радиус окружности равен 6см.
2. В треугольнике АВС АВ = 4см, ВС = 3см, АС = 5см. Докажите, что АВ – отрезок касательной, проведенной из точки А к окружности с центром в точке С и радиусом 3см.
2 ВАРИАНТ
1. Прямая NМ касается окружности с центром в точке О, М – точка касания, 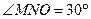 , а радиус окружности равен 5см. Найдите NО.
, а радиус окружности равен 5см. Найдите NО.
2. В треугольнике NМК NМ = 6см, МК = 8см, NК = 10см. Докажите, что МК – отрезок касательной, проведенной из точки К к окружности с центром в точке N и радиусом 6см.
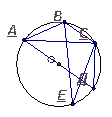
Центральные и вписанные углы. Геометрия 8.
Задачи.
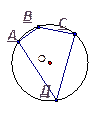
1. Дано: 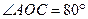 2. Дано:
2. Дано: 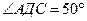
Найти: 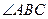 . Найти:
. Найти: 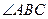 .
.
 | |||
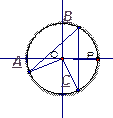 | |||
3. Дано: 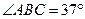 4. Дано:
4. Дано: 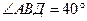
Найти: 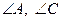 . Найти:
. Найти: 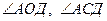 .
.
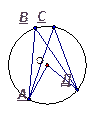
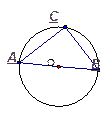
5. Дано: 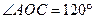 6. Дано:
6. Дано: 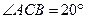
Найти: 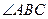 . Найти:
. Найти:  .
.
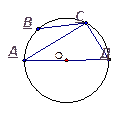
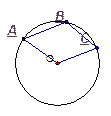
7. Дано: 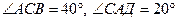 8. Дано:
8. Дано: 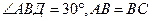
Найти: 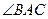 . Найти:
. Найти: 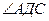 .
.
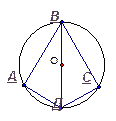
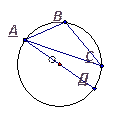
9. Дано: 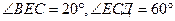
Найти: 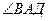 .
.