Исторические сведения о Б. Паскале.
Блез Паска́ль 1623- 1662 г.
Французский математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники. В 1641г. сконструировал суммирующую машину. Автор основного закона гидростатики. Работы по арифметике, теории чисел, алгебре, геометрии, теории вероятностей.
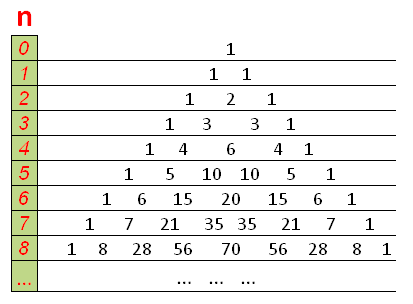
Треугольник Паскаля состоит из биномиальных коэффициентов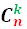 
Таблицу следует читать по строкам. В каждом горизонтальном ряду находятся биномиальные коэффициенты для определенного n , при этом k принимает значения от 0 до n .
Применим треугольник Паскаля для решения задач.
Например.
Запишите разложение двучлена, применяя треугольник Паскаля.
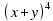
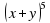
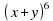
Решение:
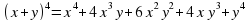берем коэффициенты из 4 строки треугольника Паскаля
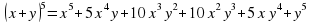из 5 строки
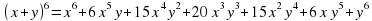из 6 строки
Если в левой части «+» поменять на «-», то знаки будут чередоваться, начиная с «+»
Треугольник Паскаля
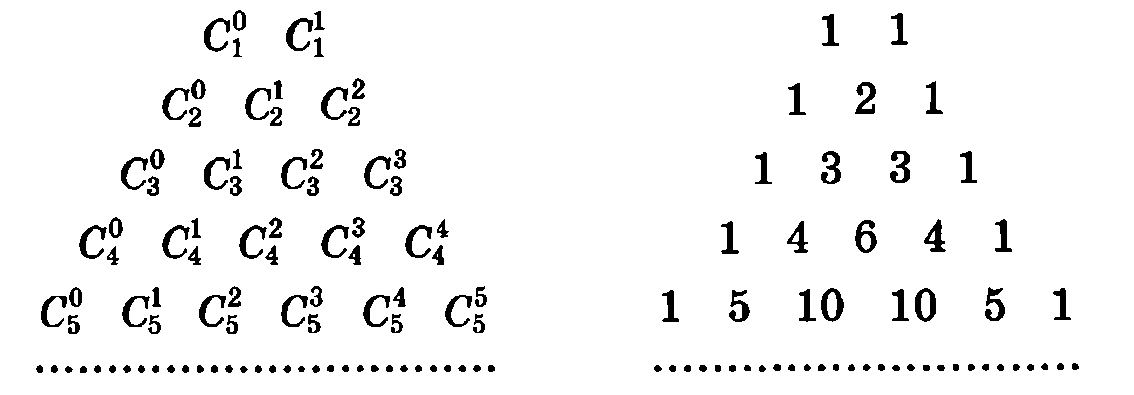
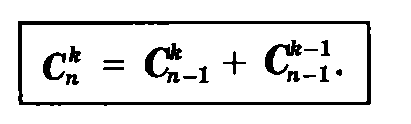
По краям треугольника стоят единицы, а остальные элементы каждой строки получаются путем сложения двух вышестоящих элементов, что приводит к ещё одному свойству сочетаний (биномиальных коэффициентов).
Применим треугольник Паскаля для решения задач.
Пример 1.
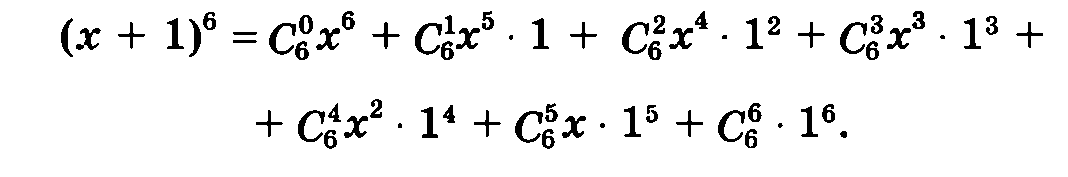
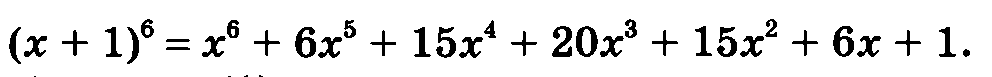
2.Запишите разложение двучлена, применяя треугольник Паскаля.
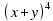
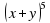
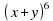
Решение:
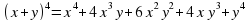берем коэффициенты из 4 строки треугольника Паскаля
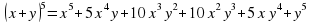из 5 строки
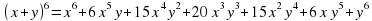из 6 строки
Если в левой части «+» поменять на «-», то знаки будут чередоваться, начиная с «+»
Домашнее задание :
1. Изучить п. 64 стр.330,сделать опорный конспект
2.Посмотреть видео уроки: https://www.youtube.com/watch?v=6TXH5pwPRH8 - видеоролик о треугольнике Паскаля
https://resh.edu.ru/subject/lesson/6119/main/285197/, https://www.youtube.com/watch?v=lbl9nxwFWDw
3. Решить : № 1092,( 2,4),1097(2,4)
Самостоятельная работа.
1 .Найти разложение бинома (рассмотреть письменно решение примеров)
№1. ( х +у)5= х5+ 5х4у + 10х3у2+ 10х2у 3+ 5ху4+ у5
№2 (1 + 2а)4= 14+ 4·13·2а + 6·12·(2а)2+ 4· 11·(2а)3+ (2а)4 =
1 + 8а + 24а2+ 32а3+ 16а4
№3 (х – у)6= (х + (-у))6= х6+ 6х5(-у) + 15х4(-у)2+ 20х3(-у)3+
15х2(-у)4+ 6х(-у)5+ у6= х6– 6х5у +15х4у2– 20х3у3 + 15х2у4– 6ху5+ у6.
2.Разложить по биному Ньютона самостоятельно:
1. ( 1 + 3а)4 =
2. (2а – в)5 =