Занятие№ 20. Тема. Формула бинома Ньютона.
Цели:
Обучающие : :формирование комбинаторного мышления через решение задач; ознакомление с треугольником Паскаля и биномом Ньютона и установление взаимосвязей между ними; изучение свойств биномиальных коэффициентов; Развивающие: формирование навыков самообразования, самореализации личности, развитие речи, мышления, памяти.
Воспитательные: привитие умений и навыков учебной работы и коллективного труда. Воспитывать умение работать самостоятельно Формирование у студентов целостного миропонимания и современного научного мировоззрения.
Средства обучения: Алимов Ш А, Колягин Ю М и др. Алгебра и начала анализа: Учебник для 10-11 кл. общеобразовательных учреждений/ М.: Просвещение, 2017.
Изучение нового материала.
Формулы сокращённого умножения являются частным случаем бинома Ньютона. Сегодня на занятии обобщим полученные знания и познакомимся с формулами:
Формула бинома Ньютона. Как возвести в степень n сумму двух слагаемых?
Рассмотрим некоторые сведения:
Исаак Ньютон был поистине Великим физиком своего времени, а может быть и величайшим физиком всех времен и народов. Но мы не будем судить об этом. Однако следует заметить, что Ньютон был еще и прекрасным математиком. Кстати формула бинома Ньютона была выгравирована на надгробии его могилы, как самое великое открытие современности того времени!
Кроме формулы бинома Ньютона, со школьной скамьи всем известна формула Ньютона-Лейбница. Таким образом, великий Ньютон вместе с Лейбницем заложили основы дифференциального и интегрального исчисления. Основы теории пределов и строгий подход в математическом анализе был начат и развивался в трудах таких гениев как Огюстен Коши, Георг Кантор, Карл Вейерштрасс. Нельзя, конечно, обойти стороной имя Леонарда Эйлера.
Но мы отвлеклись здесь от основной линии рассуждений. Ведь Формула бинома Ньютона относится к алгебре, а также к ветви математики, называемой комбинаторикой!
Вы спросите: а почему, собственно, формула бинома, и что такое бином вообще. Здесь употребляется алгебраическая терминология: в алгебре есть понятие многочлена. Многочлен это Полином - другими словами - сумма произвольного числа слагаемых называется полином.
Например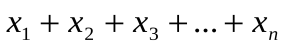 
- это полином!
итак , сумма двух слагаемых называется Бином! То есть 
- это бином, или например ( x+y) - тоже бином. Здесь x и y предполагаются неизвестными переменными величинами! Но формула бинома Ньютона на самом деле это не просто формула бинома (иначе, что это за формула такая, которая состоит из суммы двух произвольных слагаемых?). Что же он тогда изобрел?
Ньютон изобрел формулу, которая позволяет возвести сумму двух слагаемых в степень с любым показателем, а не только с показателем равным 2! Невозможно переоценить значение формулы бинома Ньютона при решении многих заданий. Поэтому правильно формула, о которой идет здесь речь, называется Формулой Ньютона для степени бинома. Мы не будем сразу писать эту формулу в общем виде, а вначале обратимся к школьной алгебре!
Вспомним из школьного курса что:
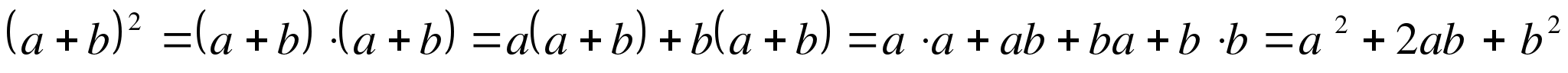
Это и есть формула квадрата суммы или формула квадрата двучлена, или формула второй степени бинома! Возведем в третью степень сумму двух слагаемых или вычислим бином третьей степени.
Скобки раскрываем аналогично, используя распределительный или дистрибутивный закон алгебры: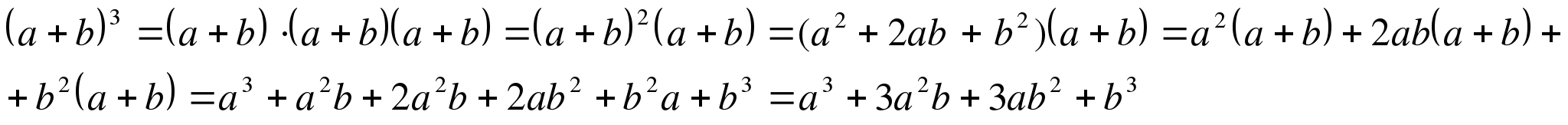 
Мы доказали формулу суммы кубов. Она нам хорошо известна из школьного курса алгебры.
Пойдем дальше, возведем бином в четвертую степень! Но возводить мы будем, воспользовавшись предыдущей формулой для третьей степени бинома:
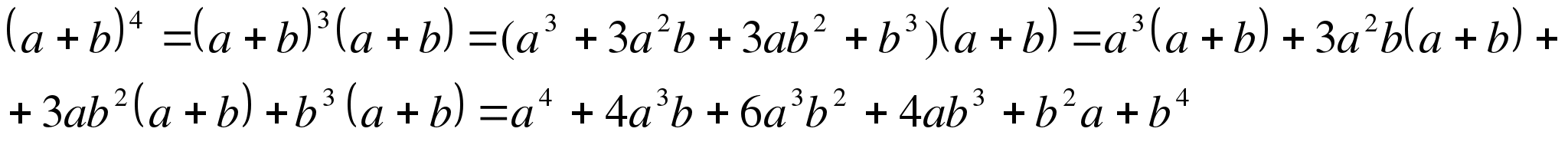
Более подробное раскрытие скобок студенты выполняют самостоятельно, проверяем результат раскрытия, так как вычисления аналогичны тому, как это уже проделали при получении формул (а + b)2 u (a+ b)3.
Итак, мы получили формулу для четвертой степени бинома! Попытаемся возвести в пятую степень бином! Для возведения бинома в пятую степень надо умножить результат возведения бинома в четвертую степень на известный нам бином! Вот в чем заключалась гениальная идея Ньютона!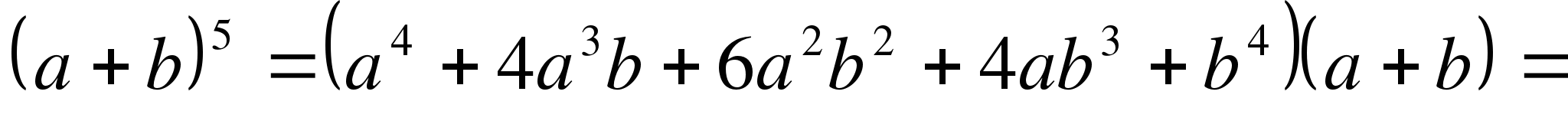 
= 
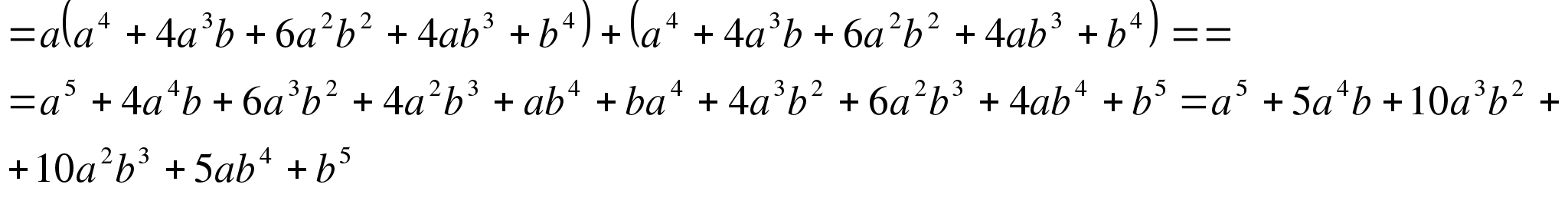
(вместо четвертой степени бинома мы подставляем вычисленное ранее выражение (a+b) 4 и снова раскрываем скобки, опуская подробные вычисления, поскольку они выполнялись при вычислении третьей и второй степени бинома.) А сколько же можно так продолжать увеличивать порядок степени возведения бинома? Ответ: до бесконечности можно! Точно также, например при n=101 умножим результат возведения в степень 100 на (а+b), тогда получим результат возведения в степень 100.
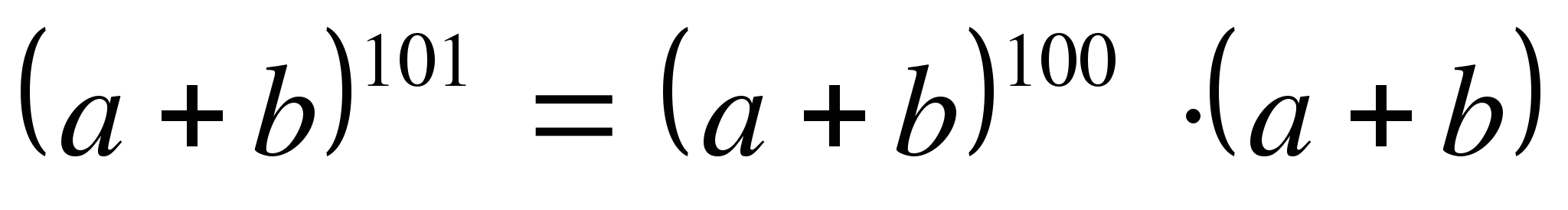
Но мы не будем расписывать все это выражение, поскольку после приведения подобных членов оно имеет 101 слагаемое и не уместится в одну строчку, а в десять строчек прочтение будет очень затруднительно!
Но гениальность Ньютона в том и заключалось, что он смог записать эту формулу в общем виде в одну строчку для любого n, то есть формулу вида:
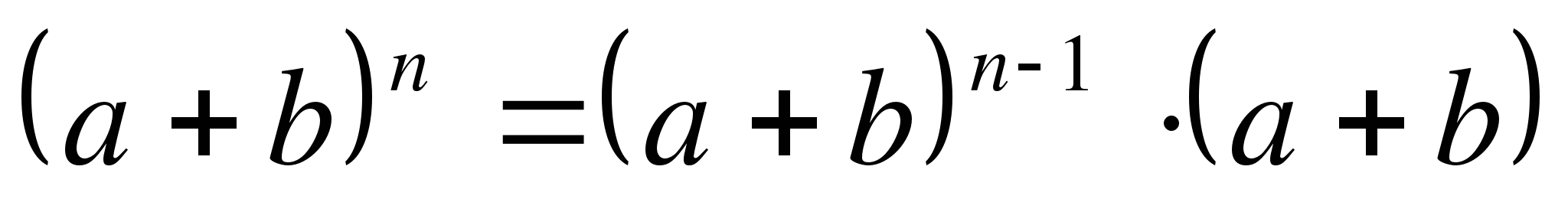
Здесь можно сделать вывод: чтобы получить формулу для степени n, надо знать эту формулу для (n-1). Чтобы знать формулу для (n-1) надо получить ее (n-1) раз так, как мы это делали для 2,3,4, и 5-й степени, то есть умножали уже известный результат для степени на единицу меньшей заданной степени на степень равную единице!
А теперь второй вывод: все эти действия, которые приводят к формуле бинома для степени ( n-1) можно записать более кратко?! Тогда можно будет не переписывать (n-1) раз фактически одни и те же вычисления для 2, 3, 4, 5, 6,...,n-1 степени бинома, а записать их одной формулой, умножить эту формулу еще раз на первую степень бинома и полностью доказать искомую формулу! Вот вам и алгоритм рассуждений Ньютона!
Здесь мы выделили последние предложения жирным шрифтом, поскольку они являются основой доказательства формулы бинома Ньютона и наиболее серьезным и сложным шагом во всех наших рассуждениях - метод математической индукции один из наиболее важных методов математики. Но как же записать общую формулу для степени бинома, равной n-1? Для ответа используем уже доказанные формулы степени бинома, равные 2, 3,4,и 5.
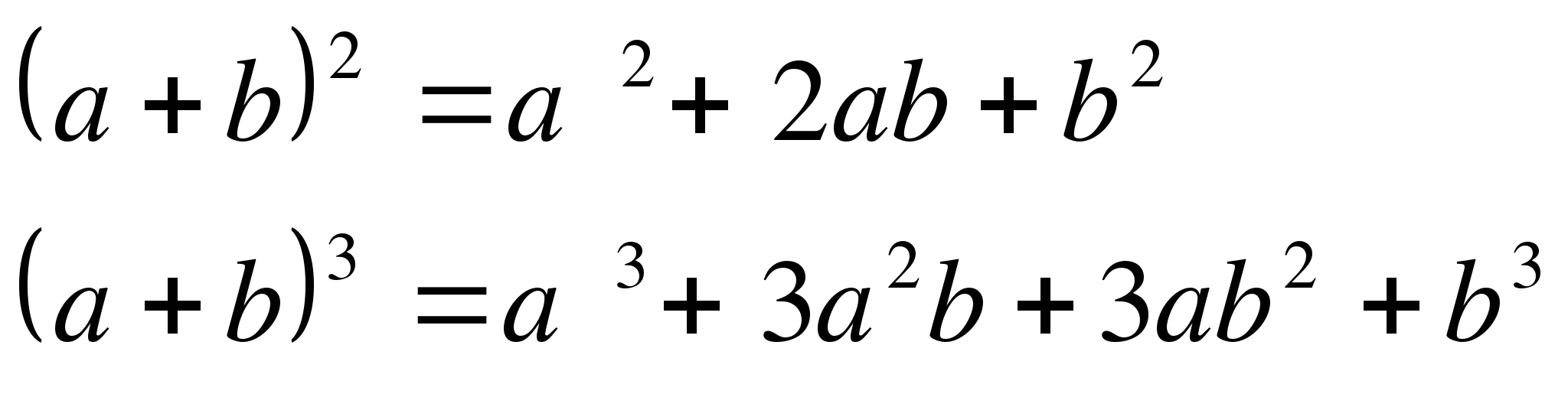
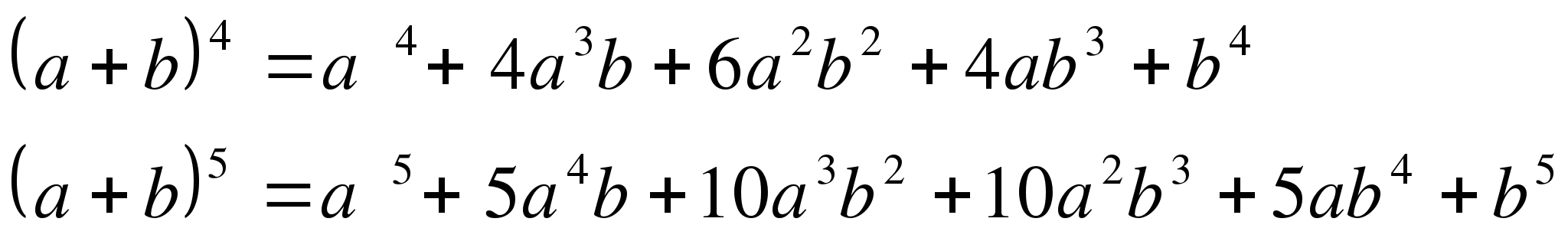
Обратим внимание, что коэффициенты крайних слагаемых равны 1, показатели степени - наивысшие (n). Показатели степени переменных изменяются в обратной зависимости, а вот определить коэффициенты достаточно сложно. Имеет смысл вернуться к определению сочетания из n элементов по m, где
n – степень бинома, а m является номером слагаемого, начиная с 0. Тогда для 3 степени бинома мы получим следующие коэффициенты:
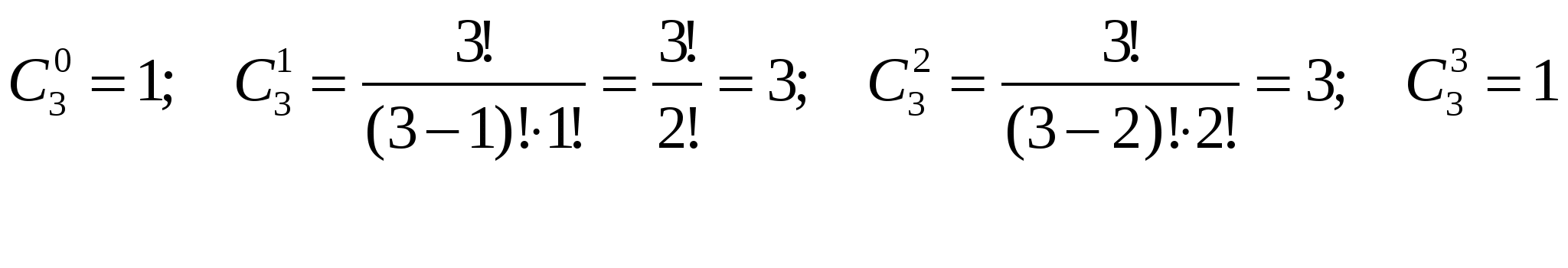
Можно, конечно, привести вывод формулы бинома, что не входит в нашу программу, поэтому запишем эту формулу без доказательства и используем ее для получения общей формулы:
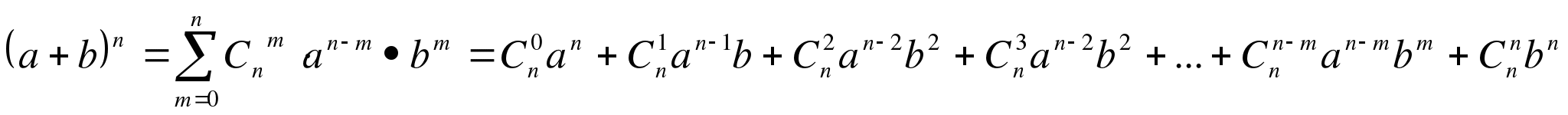
где - сигма, знак суммы слагаемых от 0 до n.
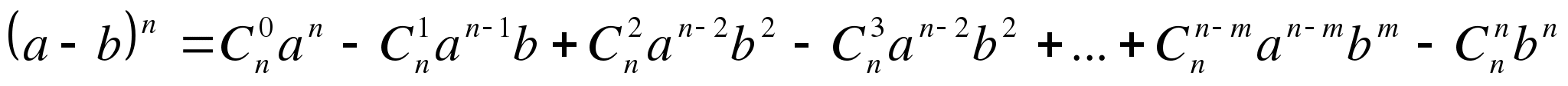
Итак, Если мы имеем бином (а - b) ⁿ, то знаки слагаемых чередуются.
Однако, вычислять коэффициенты через сочетания достаточно сложно. Чтобы облегчить эти вычисления, используют: Треугольник Паскаля:
Определение. Треугольник Паскаля - это треугольник, составленный из чисел, являющихся коэффициентами в формуле бином Ньютона.
Каждый крайний элемент равен 1, а каждый не крайний элемент равен сумме двух своих верхних соседей. (Свойство (1).
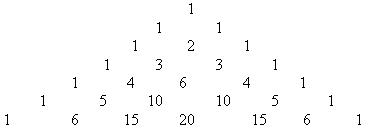
Треугольник можно продолжать до бесконечности.