“Правильные многогранники в философской картине мира Платона”
Правильные многогранники иногда называют Платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном (ок. 428 – ок. 348 до н.э.). Платон считал, что мир строится из четырёх “стихий” - огня, земли, воздуха и воды, а атомы этих “стихий” имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух. В наше время эту систему можно сравнить с четырьмя состояниями вещества - твёрдым, жидким, газообразным и пламенным. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.
Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.
Давайте, посмотрим, какие правильные многоугольники могут быть гранями правильного многогранника и сколько правильных многогранников существует.
| Форма граней | Сумма плоских углов при Вершине многогранника |

| 600 * 3 =1800 |

| 600 * 4 =2400 |

| 600 * 5 =3000 |

| 900 * 3=2700 |
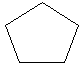
| 1080 * 3=3240 |
Всего существует пять видов правильных выпуклых многогранников. Их гранями являются правильные треугольники, правильные четырёхугольники (квадраты) и правильные пятиугольники.
Изучая любые многогранники, естественнее всего подсчитать, сколько у них граней, сколько рёбер и вершин. Подсчитаем и мы число указанных элементов правильных многогранников и занесём результаты в таблицу .
| Правильный многогранник | Число граней | Число вершин | Г+В | Число ребер |
| Тетраэдр | 4 | 4 | 8 | 6 |
| Куб | 6 | 8 | 14 | 12 |
| Октаэдр | 8 | 6 | 14 | 12 |
| Додекаэдр | 12 | 20 | 32 | 30 |
| Икосаэдр | 20 | 12 | 32 | 30 |
Названия этих многогранников пришли из Древней Греции, и в них указывается число граней: “эдра” - грань; “тетра” - 4 ; “гекса” - 6; “окта” - 8; “икоса” - 20; “додека” - 12
можно рассмотреть сумму чисел в двух столбцах, хотя бы в столбцах “грани” и “вершины” (Г + В). Заполните четвертый столбец Г+В (число граней плюс число вершин).
Формула, которая была подмечена уже Декартом в 1640 г., а позднее вновь открыта Эйлером (1752), имя которого с тех пор она носит. Формула Эйлера верна для любых выпуклых многогранников. Сумма числа граней и вершин равна числу рёбер, увеличенному на 2”, т.е. Г + В = Р + 2.
Домашнее задание:
1. Прочитать учебник: п.35,36,37 стр.75
2. Посмотреть видеоуроки https://www.youtube.com/watch?v=0B9RSxwvOaU https://www.youtube.com/watch?v=HA8WvLjBSqQ
(ОБЯЗАТЕЛЬНО!!!!!) и сделать исходя из прочитанного и увиденного опорный конспект. (выписать все виды правильных многогранников )
3. Контрольная работа№ 14. (Выполняем на двойных листочках , как обычно,ко всем задачам краткое условие и рисунок) по теме:
« Многогранники. Площади поверхности и объемы многогранников»
1. У какого многогранника один четырехгранный угол? Сделайте рисунок.
2.В основании прямой призмы лежит прямоугольный треугольник с катетами 8 см и 6 см . Определить боковое ребро призмы , если ее боковая поверхность равна 120 см2.
3.Высота правильной четырехугольной пирамиды равна 6 см .Сторона основания пирамиды -16 см. Найти боковое ребро пирамиды, площадь полной поверхности пирамиды.
4. Основание пирамиды треугольник со сторонами 13 см,14 см,15 см. Найдите ее объем ,если ее высота равна 6 см.
5. Диагональ прямоугольного параллелепипеда равна 8 см и наклонена к плоскости основания под углом 30 0. Угол между стороной и диагональю основания равен 60 0. Определите объем параллелепипеда .
Критерии оценивания контрольной работы:
Решены все задачи и к ним сделаны правильно рисунки ------ оценка 5
Есть ошибки в рисунках или не решена одна задача 3,4 или 5----оценка 4
Есть ошибки в рисунках и не решено 2 задачи ------- оценка 3








