Занятие № 40. Тема. Пирамида. Правильная пирамида.
Мотивация изучения те мы.
Мне хотелось бы начать со слов Ле Корбюдзе: «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг - геометрия».
Историческая справка
Термин «пирамида» заимствован из греческого «пирамис» или «пирамидос». Греки в свою очередь позаимствовали это слово из египетского языка. В папирусе Ахмеса встречается слово «пирамис» в смысле ребра правильной пирамиды. Другие считают, что термин берет свое начало от формы хлебцев в Древней Греции («пирос» - рожь). В связи с тем, что форма пламени напоминает образ пирамиды, некоторые ученые считали, что термин происходит от греческого слова «пир» - огонь. В Древнем Египте гробницы фараонов имели форму пирамид. Самая известная из пирамид- это пирамида Хеопса
Пирами́да Хео́пса (Хуфу) — крупнейшая из египетских пирамид, единственное из «Семи чудес света», сохранившееся до наших дней. Предполагается, что строительство, продолжавшееся двадцать лет, закончилось около 2540 года до н. э.Известны десятки египетских пирамид. На плато Гиза самые крупные из них — пирамиды Хеопса (Хуфу), Хефрена (Хафра) и Микерина (Менкаура).
· Пирамиды вокруг нас
В архитектуре часто крыши домов построены в виде пирамид.
В современной архитектуре наиболее известная пирамида- это стеклянная пирамида Лувра. Пирамида, окруженная фонтанами и еще тремя пирамидами поменьше стала одновременно входом в музей и украшением площади перед зданием. За основу пирамиды была взята пирамида Хеопса. Египетский прототип позволил создать конструкцию, идеально вместившую в себя всевозможные магазинчики, галереи, кафе и помещения для персонала. По замыслу автора пирамида у Лувра была призвана соединить небо и землю.
Цели занятия :
Обучающие: изучить новый вид многогранников – пирамиды. Выйти на понятие правильной пирамиды. Рассмотреть задачи, связанные с пирамидой и с правильной пирамидой.
Развивающие: развивать познавательный интерес через творческую активность, исследовательскую деятельность на основе умения делать обобщения по данным, полученным в результате исследования.
Воспитательные: развивать эмоционально-положительное отношение к изучению геометрии, геометрическую зоркость, способствовать развитию пространственного воображения учащихся.
Междисциплинарные связи: физика, история математики.
Список использованной литературы:
1.Геометрия, 10–11: Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 11-е изд. – М.: Просвещение, 2002 г.
2.Изучение геометрии в 10-11 классах: Метод. рекомендации к учеб.: Кн. для учителя /С. М. Саакян, В.Ф. Бутузов. – 2-е изд. – М. Просвещение, 2003. – 222 с.: ил. – ISBN 5-09-011836-1.
Изложение нового материала
1.Построение пирамиды
ü построить основания пирамиды (n-угольник)
ü за вершину можно принять любую точку, не принадлежащую сторонам основания
ü соединить отрезками вершину пирамиды со всеми вершинами основания
В случае правильной пирамиды:
ü высота изображается вертикальным отрезком
ü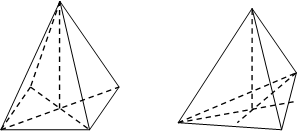 
основание высоты является центром окружности, описанной около основания
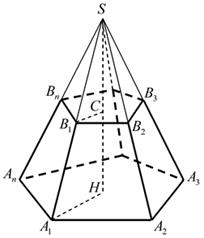
Пирамида – многогранник, составленный из n - угольника А1А2…А n и n треугольников
Пирамидой называется многогранник, который состоит из плоского многоугольника-основания пирамиды, точки, не лежащей в плоскости основания-вершины пирамиды, и всех отрезков, соединяющих вершину пирамиды с точками основания.
Элементы пирамиды.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.
Пирамида называется n -угольной, если ее основанием является n-угольник.
Треугольная пирамида называется также тетраэдром.
Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками
Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины
Все апофемы правильной пирамиды равны друг другу
Теорема о площади боковой поверхности правильной пирамиды:
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
Усеченная пирамида
Усеченной пирамидой называется многогранник, у которого вершинами служат вершины основания и вершины ее сечения плоскостью, параллельной основанию.
Свойства усеченной пирамиды:
· Основания усеченной пирамиды — подобные многоугольники.
· Боковые грани усеченной пирамиды — трапеции.
· Боковые ребра правильной усеченной пирамиды равны и одинаково наклонены к основанию пирамиды.
· Боковые грани правильной усеченной пирамиды — равные между собой равнобедренные трапеции и одинаково наклонены к основанию пирамиды.
· Двугранные углы при боковых ребрах правильной усеченной пирамиды равны.
Основные формулы
Пирамида:
Sполн = Sосн + Sбок
V = 1/3 Sосн * H, Н –высота пирамиды
Правильная пирамида:
Sбок = 1/2 Pосн * а, где а- апофема
Домашнее задание:
1. Прочитать учебник: п.32,33,34 стр. 69 - 71,
2. Посмотреть видеоуроки:
https://www.youtube.com/watch?v=Y_Z3ciD1rQM https://www.youtube.com/watch?v=J7zI2zDiAuU
https://znaika.ru/catalog/10-klass/geometry/Piramida.html
(ОБЯЗАТЕЛЬНО!!!!!) и сделать исходя из прочитанного и увиденного опорный конспект.
3. Решить задачи:
1. Площадь боковой грани правильной четырехугольной пирамиды
48 кв.см , а периметр основания -12 см . Вычислить апофему пирамиды.
2. Боковая грань правильной треугольной пирамиды –правильный треугольник периметр которого 36 см. Вычислить площадь основания пирамиды.
3. Диагональное сечение правильной четырехугольной пирамиды правильный треугольник , площадь которого равна 9 корень из 3 кв.см. Вычислить площадь основания пирамиды.