Граф является ориентированным, если для каждого ребра задано направление, в котором возможно движение по этому ребру. Если движение возможно в обоих направлениях, то граф называется неориентированным.
Графы
Графом называется множество точек (вершин), некоторые из которых соединены отрезками (ребрами).
Граф является ориентированным, если для каждого ребра задано направление, в котором возможно движение по этому ребру. Если движение возможно в обоих направлениях, то граф называется неориентированным.
Граф называется взвешенным, если каждому ребру поставлено в соответствие некоторое число (вес).
Граф называется связным, если из любой его вершины существует путь (не обязательно состоящий из одного ребра) в любую другую.
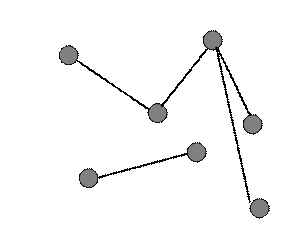
На рисунке изображен неориентированный, несвязный, невзвешенный граф.
Часть графа, которая является связной, называется компонентой связности. В графе, изображенном на рисунке две компоненты связности.
Степенью вершины (в неориентированном графе) называется количество выходящих из нее ребер.
Полустепенью вершины (в ориентированном графе) называется количество выходящих из нее ребер (полустепень исхода) или количество входящих ребер (полустепень захода).
Истоком (в ориентированном графе) называется вершина, в которую не входит ни одно ребро.
Стоком (в ориентированном графе) называется вершина, из которой не выходит ни одного ребра.
Петлей называется ребро, соединяющее вершину с самой собой.
Простым путем в графе называется путь, в котором ни одно ребро не встречается дважды.
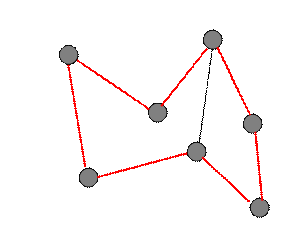
Циклом называется путь, не проходящий дважды через одну и ту же вершину. На рисунке красным цветом показаны ребра, образующие цикл.
Деревом называется граф, не содержащий циклов.
Представление графов в программах
Матрица смежности (вершины, соединенные ребром, называют смежными). Представляет собой квадратную матрицу, размерность которой равна количеству вершин графа. В i-й строке j-м столбце находится 1, если ребро ij существует, и 0 – если нет.
| 1 | 2 | 3 | 4 | |
| 1 | 1 | |||
| 2 | 1 | 1 | 1 | |
| 3 | 1 | 1 | ||
| 4 | 1 | 1 |
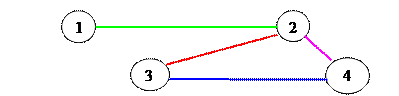
В таблице разными цветами показаны числа и ребра графа, которым они соответствуют. Матрица неориентированного графа будет симметричной относительно главной диагонали, так как в этом случае каждое ребро будет записываться дважды: как ij и как ji. Для взвешенного графа в матрице могут указываться веса соответствующих ребер.
Список ребер (таблица, высота которой равна количеству ребер; в первом столбце указана вершина, из которой выходит ребро, во втором – номер вершины, в которую входит ребро).
| V1 | V2 |
| 1 | 2 |
| 2 | 3 |
| 2 | 4 |
| 3 | 4 |
Данная таблица представляет собой список ребер для предыдущего примера (включать ли в список ребер в случае неориентированного графа каждое ребро дважды или только один раз - зависит от конкретной задачи).