5 Порядок расчета неопределенности измерений
Для оценивания неопределенности можно использовать следующий алгоритм:
Этап 1. Описание измеряемой величины.
На первом этапе оценки определяют, что и как собираются измерять. В большинстве случаев измеряемая величина Y не измеряют непосредственно, а определяют через N других величин Х1, Х2 ....., ХN и выражаются через функциональную зависимость
Y = f (Х1, Х2 ....., ХL),
где Х1, Х2 ....., ХN - входные величины, Y - выходная величина
Входные величины Х1, Х2 ....., ХN, от которых зависит выходная величина Y, являются непосредственно измеряемыми величинами и они могут зависеть от других величин Х1 = f (Z1,Z2 ....., ХN), Х2 = f (V1.V2 ....., VK), включая поправки и поправочные коэффициенты на систематические эффекты, что усложняет вид функциональной зависимости f.
Входные величины Х1, Х2 ....., ХN могут быть разделены на две группы:
1. величины, значения и неопределенности которых определяют непосредственно в текущем измерении. Эти значения и неопределенности можно получить, например, в результате однократного измерения, повторных измерений или по основанным на опыте суждениям. Они могут включать определения поправок к показаниям приборов и поправок на влияющие величины, такие как окружающая температура, атмосферное давление и влажность
2. величины, значения и неопределенности которых получены из сторонних источников. К ним относятся величины, связанные с аттестованными эталонами, стандартными образцами веществ и материалов, а также величины, значения которых указаны в справочниках
Этап 2. Выявление источников неопределенности.
При составлении списка источников неопределенностей обычно удобно начать с основного выражения, используемого для вычисления результата из промежуточных величин. Все параметры в этом выражении могут быть источниками неопределенности. Также можно рассмотреть методику измерений в виде последовательных операций, определяя неопределенность каждой такой операции. Типичными источниками неопределенности могут быть другие параметры, которые в явном виде не входят в выражение:
а) пробоотбор - учитывается, когда отбор пробы является частью методики выполнения измерений (отбор проб в поглотительные трубки и т.д.), т.е. может появиться смещение между двумя отобранными параллельными пробами;
| ФБУЗ «Центр гигиены и эпидемиологии в Забайкальском крае» | |
| ДП 03-3.1-11-02-2019 | Лист 7 |
| Листов 18 | |
б) условия хранения - когда анализируемые пробы хранятся в течение какого-то времени и условия хранения могут повлиять на результат (например, определение кислотности в пищевых продуктах, определение
влажности в хлебобулочных изделиях). Продолжительность хранения рассматриваются как источник неопределенности.
в) аппаратурные эффекты, включающие в себя:
- точность аналитических весов;
- погрешность параметров микроклимата и т.д.;
- точность лабораторной посуды;
- точность дозирующих инструментов (пипетки, механические дозаторы) и т.д.;
г) чистота реактивов, ГСО, воды, используемой в качестве разбавителя.
д) влияние матрицы пробы: при сложном составе матрицы оказывается влияние на качество извлечения определяемого компонента и на отклик прибора при определении концентраций; стабильность пробы или определяемого компонента.
е) условия измерений – мерная стеклянная посуда может применяться, при температуре отличающейся от той, при которой она была откалибрована. Аналогично может иметь значение влажность окружающего воздуха, если применяемые материалы, чувствительны к ее возможным изменениям.
ж) вычислительные эффекты - например, выбор неподходящей модели при градуировке (выбор линейной градуировки при нелинейном отклике), неправильное округление промежуточных результатов и т.д.
з) поправка на холостую пробу, что является особенно важным при анализе следов присутствия определяемого компонента.
и) влияние оператора - возможность регистрации заниженных или завышенных показаний измерительных приборов, возможность незначительных различий в интерпретации методики.
При оценивании неопределенности необходимо производить суммирование стандартных неопределенностей входных величин.
Этап 3. Упрощение, вследствие объединения составляющих, охватывае-мых имеющимися данными. Оценивание сгруппированных составляющих. Оценивание оставшихся составляющих.
На этом этапе происходит количественное описание неопределенности, возникающей от выявленных источников. Это может быть сделано путем:
- оценивания неопределенности, возникающей от каждого отдельного источника, и последующего суммирования составляющих;
- непосредственного определения суммарного вклада в неопределенность от некоторых или всех источников с использованием данных о метрологических характеристиках метода.
| ФБУЗ «Центр гигиены и эпидемиологии в Забайкальском крае» | |
| ДП 03-3.1-11-03-2021 | Лист 8 |
| Листов 18 | |
В зависимости от используемых данных, методика вычисления неопределенности может отличаться. Различают два типа вычисления стандартной неопределенности:
- вычисление по типу А – путем статистического анализа результатов многократных измерений;
- вычисление по типу В – с использованием других способов.
Расчет стандартной неопределенности, оцениваемой по типу А - uA
Аналог – «случайная погрешность». Объединяет в себе факторы неопределённости случайного характера – изменение внешних условий, «дрожание рук» и т.п.. Для оценки стандартной неопределённости по типу А используют статистические методы – то есть, необходимо провести несколько измерений одной и той же величины, которые затем подвергнуть статистической обработке. В результате такой обработки, в идеале, влияние случайных факторов неопределённости на результат измерений будет минимизировано. Стандартную неопределённость типа А количественно характеризуется дисперсией и стандартным отклонением.
Оценку измеряемой величины Среднее арифметическое значение 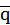 из n измерений:
из n измерений:
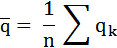
где n - число независимых измерений 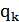 , полученных при постоянных условиях измерений.
, полученных при постоянных условиях измерений.
Разброс измерений qk обусловлен случайными изменениями влияющих величин. Выборочную дисперсию s2(qk), являющуюся оценкой дисперсии σ2 для данного распределения вероятностей величины q. Получают по формуле:
s2(qk)= 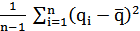
Положительный квадратный корень s(qk) из выборочной дисперсии называют выборочным стандартным отклонением. Эта величина характеризует изменчивость измерений или, точнее, их разброс относительно среднего значения 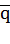 .
.
Наилучшей оценкой дисперсии среднего значения является:
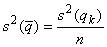
Таким образом, стандартная неопределенность uA. полученную по n независимым повторным измерениям определяют по формуле:
uA= 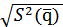
| ФБУЗ «Центр гигиены и эпидемиологии в Забайкальском крае» | |
| ДП 03-3.1-11-03-2021 | Лист 9 |
| Листов 18 | |
Расчет стандартной неопределенности, оцениваемой по типу В.
Аналог - «систематическая погрешность». Объединяет в себе факторы неопределённости заведомо известного характера (постоянные или переменные величины, изменяющиеся по известным законам).
В качестве исходных данных для вычисления uВ используют:
- данные предшествующих измерений величин, входящих в уравнение измерения; сведения о виде распределения вероятностей;
- данные, полученные опытным или теоретическим путем, сведения о свойствах материалов и характеристиках приборов;
- характеристики, заявляемые изготовителем СО, СИ, ИО, ВО;
- данные, приводимые в свидетельствах о поверке или калибровке и других документах;
- неопределенности величин, которые вместе со значениями этих величин приведены в справочных данных.
Неопределенности этих данных обычно представляют в виде границ отклонения значения величины от ее оценки. Формулы для вычисления стандартной неопределенности по типу В различаются в зависимости от вида распределения возможных значений этих величин. Наиболее часто встречаются следующие формы распределения: прямоугольная, треугольная и нормальная (таблица № 1).
Таблица №1
| Форма распределения | Случаи применения | Формулы для расчета стандартной неопределенности по типу В | Пример |
| Прямоугольная | - В сертификате или иной технической документации пределы границ погрешности (допустимой ошибки), без указания доверительной вероятности; - Оценка неопределенности дана в виде максимального диапазона (±а), с неизвестной формой распределения |
uВ = 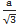
| Весы аналитические
AND HR-250A/ Поверка подтверждает границы погрешности Δ=±500 мкг, без указания доверительной вероятности
uВ = 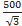 =289 мкг =289 мкг
|
| Треугольная | - Информация может быть приведена в виде максимального интервала (±а), описывается симметричным распределением, без указания доверительной вероятности. Значения в центре интервала более вероятны, чем вблизи его границ. - Обычно это - для мерной посуды, прошедшей поверку или калибровку | uВ = 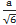
| Пипетка мерная 1-го класса точности с делениями (по ГОСТ 20292-74) V=1,0 см3. Допустимая погрешность равна ±0,006 см3.
uВ = 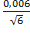 =0,00245 см 3 =0,00245 см 3
|
| ФБУЗ «Центр гигиены и эпидемиологии в Забайкальском крае» | |
| ДП 03-3.1-11-03-2021 | Лист 10 |
| Листов 18 | |
Продолжение таблицы 1
| Форма распределения | Случаи применения | Формулы для расчета стандартной неопределенности по типу В | Пример |
| Нормальная | - В технической документации указан доверительный интервал (Р=0,95; 0,99…) - Оценка проведена на основе повторных измерений величины; - Неопределенность задана в виде расширенной неопределенности; - Неопределенность задана в виде стандартного отклонения. | - неопределенность дана в виде предела допускаемой погрешности:
uВ = 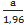 (при 95%)
uВ = (при 95%)
uВ =  (при 99,7%)
- неопределенность дана в виде СКО: U(в)= (при 99,7%)
- неопределенность дана в виде СКО: U(в)= 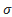
| ГСО состава водного раствора нитрит-ионов. Массовая концентрация нитрит-ионов 1,01 г/дм3, границы относительной погрешности при Р=0,95 составляют ±1,0 % uВ =1,01*0,01/1,96 = 0,056 г/дм3 |
Расчет суммарной стандартной неопределенности результата измерения
Суммарная стандартная неопределенность (uc) - стандартное отклонение результата конкретного измерения или серии измерений, которое учитывает одну или более составляющую неопределенности.
Суммарная стандартная неопределенность результата измерения одновременно учитывает влияние случайных и известных факторов неопределённости. По сути, суммирует все факторы неопределённости, с учётом их вклада в результат измерений.
Суммарную с тандартную неопределенность ис(у) представляют собой положительный квадратный корень из суммарной дисперсии, получаемой по формуле:
ис(у) = 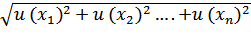
где, 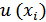 - стандартная неопределенность входной величины, оцененная по типу А и/или по типу В.
- стандартная неопределенность входной величины, оцененная по типу А и/или по типу В.
Поскольку для расчета суммарной стандартной неопределенности непринципиально, как были получены оценки ее составляющих, то и информация о способах получения оценки неопределенности заимствованного значения не является существенной.
Если оценка входной величины получена в результате единичного измерения с использованием средства измерения, то оценка неопределенности в основном будет связана с повторяемостью результатов измерений. Оценку составляющей неопределенности для данной величины следует основываться на характеристиках используемого средства измерений.
| ФБУЗ «Центр гигиены и эпидемиологии в Забайкальском крае» | |
| ДП 03-3.1-11-03-2021 | Лист 11 |
| Листов 18 | |
Этап 4. Вычисление расширенной неопределенности.
Хотя параметр ис(у) может служить универсальным средством выражения неопределенности результата измерения, зачастую в промышленности, торговле и законодательно регулируемых областях, например связанных с охраной здоровья и обеспечением безопасности, результат измерений должен быть представлен с указанием охватывающего его интервала, в пределах которого, как можно ожидать, будет находиться большая часть распределения значений, которые обоснованно могут быть приписаны измеряемой величине.
Дополнительной мерой неопределенности, которая удовлетворяет требованию представления интервала является расширенная неопределенность , обозначаемая символом U.
Расширенную неопределенность получают умножением суммарной стандартной неопределенности uc(y) на коэффициент охвата k:
U=k·uc(y)
Для большинства случаев следует брать коэффициент охвата k, равный 2 который соответствует интервалу с уровнем доверия, близким к 95%, а значение k=3 – интервалу с уровнем доверия, близким к 99%.
Однако в случаях, когда суммарная стандартная неопределенность основана на результатах статистических наблюдений с небольшим числом измерений, коэффициент охвата - k следует брать равным двустороннему значению критерия Стьюдента - tр , зависящее от числа степеней свободы ν , такое что доля р распределения Стьюдента попадает в интервал от - tр(ν) до + tр(ν). Таким образом, расширенная неопределенность имеет формулу:
U=k·uc(y)=tр uc(y)
Значения tр(ν) t- распределения с числом степеней свободы ν, определяющие интервал от - tр(ν) до + tр(ν), в пределах которого находится доля р распределения случайной переменной указана в таблице G.2 ГОСТ 34100.3-2017.








