Справочный материал для решения экономических задач
Виды экономических задач:
1) Кредиты с равными (аннуитетными) платежами (аннуитет – начисление равных платежей на весь срок погашения кредита. При этом в первой половине срока задолженность по кредиту практически не гасится – выплачиваются в большей части проценты. Эта особенность делает платежи относительно небольшими, но увеличивает общую сумму начисляемых процентов).
2) Кредиты с дифференцированными платежами (характерны тем, что задолженность по кредиту погашается равномерно, начиная с самых первых выплат, а проценты начисляются на фактический остаток. Таким образом, каждый последующий платеж меньше предыдущего).
3) Вклады, сложные проценты.
4) Оптимальный выбор.
Определение: один процент – это одна сотая доля. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь.
При решении задач необходимо понимать механизм начисления процентов по вкладам или кредитам. Например, если банк выдаёт кредит (S) клиенту, то через год клиент должен банку не только сумму кредита, но и некий процент (r). Возникает необходимость введения нового коэффициента k, k=1+0,01r. С учётом этого, долг клиента банку через год можно записать следующим образом:
S + r% от S = S + 0,01r 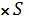 = S (1 + 0,01r) = kS
= S (1 + 0,01r) = kS
При решении задач, связанных с аннуитетными платежами удобно использовать таблицы:
S – сумма кредита, r% - годовые (ежемесячные) проценты
b=1+0,01r – коэффициент, х – ежегодная (ежемесячная) выплата
| Год | Долг с % | Выплата | Долг после выплаты |
| 0 | S | ||
| 1 год | Sb | x | Sb-x |
| 2 год | (Sb-x)b=Sb2-xb | x | Sb2-xb-x |
| 3 год | (Sb2-xb-x)b=Sb3-x b2-xb | x | Sb3-x b2-xb-x |
| 4 год | (Sb3-x b2-xb-x)b= Sb4-xb3-xb2-xb | x | Sb4-xb3-xb2-xb-x |
| 5 год | (Sb4-xb3-xb2-xb-x)b= Sb5-xb4-xb3-xb2-xb | x | Sb5-xb4-xb3-xb2-xb-x |
| 6 год | (Sb5-xb4-xb3-xb2-xb-x)b= Sb6-xb5-xb4-xb-3xb2-xb | x | Sb6-xb5-xb4-xb-3xb2-xb-x |
| n год | Sbn-xbn-1-xbn-2-…-xb2-xb | x | Полная выплата, долг равен 0 |
При решении задач, связанных с дифференцированными платежами, удобно пользоваться следующей таблицей:
| Месяц | Долг с % | Выплата | Долг после выплаты |
| 0 | S | ||
| 1 | Sb | Sb 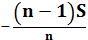
| 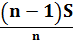
|
| 2 | 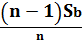
| 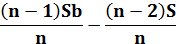
| 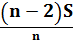
|
| n-1 | 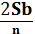
| 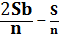
| 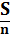
|
| n | 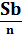
| 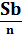
| 0 |
При решении задач по теме «Вклады»:
| Год | Вклад с % |
| 0 | |
| 1 | Sb |
| 2 | Sb2 |
| n | Sbn |
При решении задач, в которых осуществлялись какие-либо действия (пополнение или снятие денег с вклада):
х – действие
| Год | Вклад с % | Действие | Вклад после действия. |
| 0 | S | ||
| 1 год | Sb | +х | Sb+x |
| 2 год | b(Sb+x)= Sb2+xb | +х | Sb2+xb+x |
| 3 год | b(Sb2+xb+x)=Sb3_+хb2+xb | Снял вклад |
Кредиты с равными (аннуитетными) платежами.
Общая схема решения


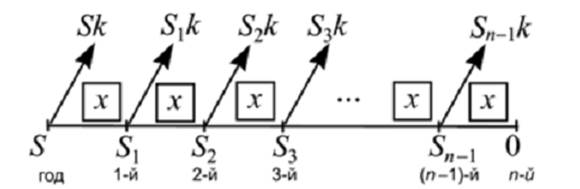
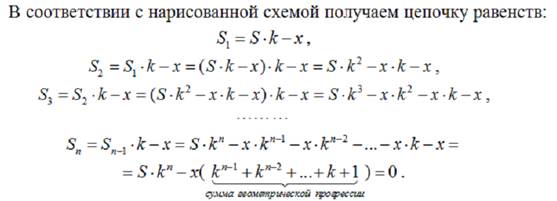
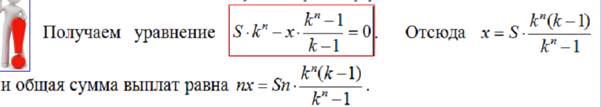
Кредиты с дифференцированными платежами
Схема 2 – уменьшение долга каждый год на одну и ту же величину


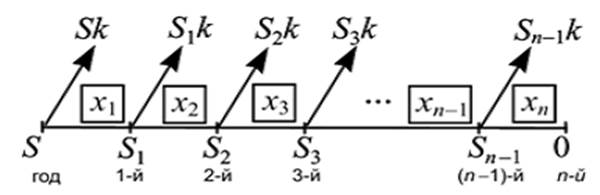


Арифметическая прогрессия
Определение. Последовательность чисел, в которой каждое следующее отличается от предыдущего ровно на одну и ту же величину, называется арифметической прогрессией.
Любой член арифметической прогрессии вычисляется по формуле:
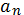 =
= 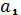 + (n-1)d
+ (n-1)d
Формула суммы n-первых членов арифметической прогрессии
Sn = 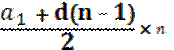
Геометрическая прогрессия
Определение. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.
Любой член геометрической прогрессии вычисляется по формуле:
bn =b1· qn-1
Формула суммы n-первых членов геометрической прогрессии
Sn=