Клаузиус (1850 г.) сформулировалвторой закон термодинамики так: невозможен процесс, при котором теплота переходила бы самопроизвольно от тел более холодных к телам более горячим.

Дата: 2025-05-25; Просмотры: 7
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

У. Томсон (Кельвин) (1851 г.) предложил следующую формулировку: невозможно построить периодически действующую машину, вся деятельность которой сводилась бы к совершению механической работы и соответствующему охлаждению резервуара.

Постулат Томсона может быть сформулирован и так: вечный двигатель второго рода невозможен. Вечным двигателем второго рода называют устройство, которое без компенсации полностью превращало бы периодически теплоту какого-либо тела в работу (В.Оствальд). Под компенсациейпонимают изменение состояния рабочего тела или отдачу части теплоты рабочим телом другим телам и изменение термодинамического состояния этих тел при круговом процессе превращения теплоты в работу.

Второй закон термодинамики устанавливает, что без компенсации в круговом процессе ни один джоуль теплоты нельзя превратить в работу.Работа же превращается в теплоту полностью без всякой компенсации. Последнее связано, как отмечалось ранее, с самопроизвольностью процесса рассеивания (обесценивания) энергии.

Второй закон термодинамики вводит функцию состояния системы, которая количественно характеризует процесс рассеивания энергии. В этом смысле приведенные формулировки второго закона термодинамики равноценны, ибо из них следует существование функции состояния системы – энтропии.

В настоящее время второй закон термодинамикиформулируется следующим образом: существует аддитивная функция состояния системы S – энтропия, которая следующим образом связана с теплотой, поступающей в систему, и температурой системы:

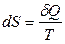для обратимых процессов; (3.2)

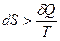для необратимых процессов. (3.3)

Таким образом, при обратимых процессах в адиабатически изолированной системе ее энтропия не изменяется (dS = 0), а при необратимых процессах увеличивается (dS > 0).

В отличие от внутренней энергии значение энтропии изолированной системы зависит от характера происходящих в ней процессов: в ходе релаксации энтропия изолированной системы должна возрастать, достигая максимального значения при равновесии.

В общем виде второй закон термодинамики для изолированной системы записывается так:

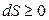. (3.4)

Энтропия изолированной системы или увеличивается, если в ней протекают самопроизвольные необратимые процессы, или остается постоянной. Поэтому второй закон термодинамики определяют также как закон о неубывании энтропии в изолированных системах.

Таким образом, второй закон термодинамики дает критерий самопроизвольности процессов в изолированной системе. Спонтанно в такой системе могут протекать только процессы, сопровождающиеся увеличением энтропии. Самопроизвольные процессы заканчиваются с установлением равновесия в системе. Значит, в состоянии равновесия энтропия изолированной системы максимальна. В соответствии с этим критерием равновесия в изолированной системе будет

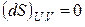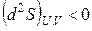, . (3.5)

Если в процессе принимает участие неизолированная система, то для оценки необратимости (самопроизвольности) процесса необходимо знать изменение энтропии системы dS1 и изменение энтропии окружающей среды dS2. Если принять, что система и окружающая среда (их часто называют «вселенной») образуют изолированную систему, то условием необратимости процесса будет

,

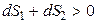то есть процесс будет необратим, если общее изменение энтропии системы и окружающей среды будет больше нуля.

Окружающая среда – огромный резервуар; eе объем и температура не изменяются при теплообмене с системой. Поэтому можно для окружающей среды приравнять δQ = dU и не важно, обратимо или необратимо происходит переход теплоты, так как и δQобр, и δQнеобр точно равны dU окружающей среды. Таким образом, изменение энтропии окружающей среды всегда равно:

.

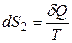Второй закон термодинамики: Невозможен самопроизвольный переход от тела менее нагретого к более нагретому. Невозможно превратить теплоту в работу не приводя никакого другого действия, кроме охлаждения источника тепла. Вечный двигатель 2-го рода невозможен, т. е. такой двигатель, результатом которого было бы получение работы за счет тепла окружающей среды. Все самопроизвольные процессы в макроскопических системах протекают в направлении от менее вероятного к более вероятному состоянию системы. Обратимые – такие термодинамические процессы, при которых возвращение системы в первоначальное состояние не требует затраты энергии извне и связанных с этим изменений в окружающей среде. Необратимые – термодинамические процессы, при которых возвращение системы в исходное состояние возможно лишь при условии затрат внешней энергии, что влечет за собой определенные изменения в окружающей среде. Энтропия(S) характеризует меру беспорядка в расположении и поведении частиц составляющих систему, а также меру стремления частиц занять как можно больший V. Чем больше беспорядка, тем выше энтропия. ∆S0=∑vj(ню) S0(прод) - ∑vj(ню) S0(исх.в-в) Энергия Гиббса(G) - часть внутренней энергии системы которая может быть переведена в работу. Под стандартной энергией Гиббса образования ΔG°, понимают изменение энергии Гиббса при реакции образования 1 моль вещества, находящегося в стандартном состоянии. Это определение подразумевает, что стандартная энергия Гиббса образования простого вещества, устойчивого в стандартных условиях, равна нулю. В самопроизвольной реакции: ∆G<0 (G2-G1<0) ∆S>0 (S2-S1>0) реакция пойдет → ∆G>0 ∆S<0 реакция пойдет ← Формула для I и II т/д: ∆Gт=∆H0хр - Т∆S Энтальпийный и энтропийный факторы Из приведенного выражения следует, что самопроизвольное течение реакции может контролироваться как энтальпийным (∆H), так и энтропийным фактором (T∆S). Очевидно, что для реакций, характеризующихся ∆Hr< 0 и ∆Sr> О, энергия Гиббса должна обязательно убывать, т. е. ∆Gr< 0, и такие реакции могут протекать самопроизвольно при любых температурах, так как оба фактора способствуют протеканию процесса. Пример такой реакции — гидролиз белка. Наоборот, при ∆Hr> 0 и ∆Sr< 0 самопроизвольное течение реакций всегда невозможно, так как энергия Гиббса должна обязательно возрастать. Оба фактора препятствуют протеканию реакции. Пример — фотосинтез, т. е. образование глюкозы и кислорода из углекислого газа и воды. Несогласованное действие факторов наблюдается в двух случаях: 1) ∆Hr> 0 и ∆Sr> 0 — самопроизвольному протеканию реакции способствует энтропийный фактор, отрицательное значение изменения энергии Гиббса возможно при соотношении |∆Sr |> |∆Hr|, т. е. при достаточно высоких температурах. Примером процессов этого типа является тепловая денатурация белков; 2) ∆Hr< О и ∆Sr< О — благоприятствующим фактором является энтальпийный, соотношение AGT< 0 наблюдается при |∆Hr| >|∆Sr |, т. е. при достаточно низких температурах. Пример процессов этого типа — гидратация белков. Вопрос 5-6. Предмет и основные понятия химической кинетики. Химическая кинетика как основа для изучения скоростей и механизмов биохимических процессов. Скорость реакции. Классификация реакций, применяющиеся в кинетике: реакции гомогенные, гетерогенные; реакции простые и сложные. Молекулярность реакции. Кинетические уравнения. Порядок реакции. Период полупревращения.
ГЕЛЬМГОЛЬЦА ЭНЕРГИЯ (свободная энергия, изохорно-изотермический потенциал) - один изтермодинамических потенциалов, характеристическая функция при выборе объёма V и темп-ры T в качестве независимых термодинамич. переменных. Введена Дж. У. Гиббсом (J. W. Gibbs) в 1875, её использовал Г. Гельмгольц в 1882, к-рому принадлежит термин "свободная энергия". В статистич. физике более распространён термин "свободная энергия".

Существование Г. э. есть следствие первого и второго начал термодинамики. Она связана свнутренней энергией U и энтропией S соотношением F=U-TS (для Г. э. используют также обозначения Аили 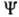). Изменение Г. э. при квазистатич. процессе равно 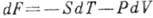, следовательно, убыль Г. э. при изотермич. процессе равна полной работе, совершаемой системой. Энтропию и давление можно получить, дифференцируя Г. э. по T и V: 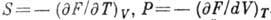. Это означает, что Г. э. есть характеристич. ф-ция в переменных T и V. Для многокомпонентных систем 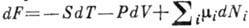, где dNi - приращение массы i-гo компонента, 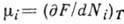,v - хим. потенциал. Условием термодинамич. равновесия системы является минимум Г. э. при постоянствеT, V и др. термодинамич. параметров, определяющих состояние системы.

В статистич. физике Г. э. определяется через логарифм 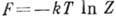статистич. интеграла (или статистич. суммы) Z:

 

Вопрос 18

 

Обратимые – такие термодинамические процессы, при которых возвращение системы в первоначальное состояние не требует затраты энергии извне и связанных с этим изменений в окружающей среде. Необратимые – термодинамические процессы, при которых возвращение системы в исходное состояние возможно лишь при условии затрат внешней энергии, что влечет за собой определенные изменения в окружающей среде.

ХИМИЧЕСКОЕ РАВНОВЕСИЕ.

Химическое равновесие - состояние системы, в котором скорость прямой реакции (V1) равна скорости обратной реакции (V2). При химическом равновесии концентрации веществ остаются неизменными. Химическое равновесие имеет динамический характер: прямая и обратная реакции при равновесии не прекращаются.

Состояние химического равновесия количественно характеризуется константой равновесия, представляющей собой отношение констант прямой (K1) и обратной (K2) реакций.

Для реакции mA + nB « pC + dD константа равновесия равна

 

K = K1 / K2 = ([C]p • [D]d) / ([A]m • [B]n)

 

Константа равновесия зависит от температуры и природы реагирующих веществ. Чем больше константа равновесия, тем больше равновесие сдвинуто в сторону образования продуктов прямой реакции. В состоянии равновесия молекулы не перестают испытывать соударения, и между ними не прекращается взаимодействие, но концентрации веществ остаются постоянными. Эти концентрации называются равновесными.

Равновесная концентрация - концентрация вещества, участвующего в обратимой химической реакции, достигшей состояния равновесия.

Равновесная концентрация обозначается формулой вещества, взятой в квадратные скобки, например:

сравновесная (Н2) = [H2] или равновесная(HI) = [HI].

Как и любая другая концентрация, равновесная концентрация измеряется в молях на литр.
Если бы в рассмотренных нами примерах мы взяли другие концентрации исходных веществ, то после достижения равновесия получили бы другие значения равновесных концентраций. Эти новые значения (обозначим их звездочками) будут связаны со старыми следующим образом:

.

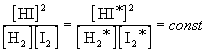В общем случае для обратимой реакции

aA + bB dD + fF

в состоянии равновесия при постоянной температуре соблюдается соотношение

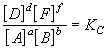
Это соотношение носит название закон действующих масс, который формулируется следующим образом:

при постоянной температуре отношение произведения равновесных концентраций продуктов реакции, взятых в степенях, равных их коэффициентам, к произведению равновесных концентраций исходных веществ, взятых в степенях, равных их коэффициентам, есть величина постоянная.

Постоянная величина (КС) называется константой равновесия данной реакции. Индекс " с" в обозначении этой величины показывает, что для расчета константы использовались концентрации.
Если константа равновесия велика, то равновесие сдвинуто в сторону продуктов прямой реакции, если мала, то - в сторону исходных веществ. Если константа равновесия очень велика, то говорят, что реакция "практически необратима", если константа равновесия очень мала, то реакция " практически не идет".
Константа равновесия - для каждой обратимой реакции величина постоянная только при постоянной температуре. Для одной и той же реакции при разных температурах константа равновесия принимает разные значения.
Приведенное выражение для закона действующих масс справедливо только для реакций, все участники которых представляют собой либо газы, либо растворенные вещества. В других случаях уравнение для константы равновесия несколько меняется.
Например, в протекающей при высокой температуре обратимой реакции

С (гр) + СО2 2СО (г)

участвует твердый графит С (гр). Формально, пользуясь законом действующих масс, запишем выражение для константы равновесия этой реакции, обозначив ее К':

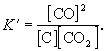
Твердый графит, лежащий на дне реактора, реагирует только с поверхности, и его " концентрация" не зависит от массы графита и постоянна при любом соотношении веществ в газовой смеси.
Умножим правую и левую части уравнения на эту постоянную величину:

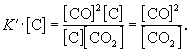
Получившаяся величина и есть константа равновесия этой реакции:

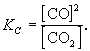
Аналогичным образом, для равновесия другой обратимой реакции, протекающей также при высокой температуре,

CaCO3(кр) СаО (кр) + СО2(г),

получим константу равновесия

КС = [CO2].

В этом случае она просто равна равновесной концентрации углекислого газа.
С метрологической точки зрения константа равновесия не является одной физической величиной. Это группа величин с различными единицами измерений, зависящими от конкретного выражения константы через равновесные концентрации. Например, для обратимой реакции графита с углекислым газом [Kc] = 1 моль/л, такая же единица измерений и у константы равновесия реакции термического разложения карбоната кальция, а константа равновесия реакции синтеза йодоводорода - величина безразмерная. В общем случае [Kc] = 1 (моль/л)n.

Принцип Ле Шателье — Брауна (он же Принцип Ле Шателье) — термодинамический принцип подвижного равновесия, который описывает влияние, которое оказывается на систему внешним воздействием и может быть сформулирован следующим образом: