Непосредственное интегрирование– интегрирование с использованием таблицы неопределенных интегралов, основных свойств и тождественных преобразований подынтегральной функции
Пример 1 . Сначала приведем полное решение:
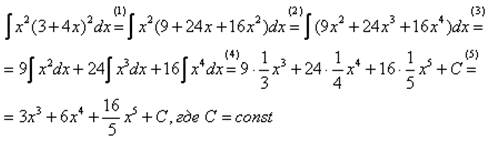
Пример 2 . Найти неопределенный интеграл 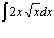 .
.
Используя свойство неопределенного интеграла, вынесем за знак интеграла постоянную 2. Затем, выполняя элементарные математические преобразования, приведем подынтегральную функцию к степенному виду:
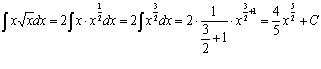 .
.
Пример 3 .
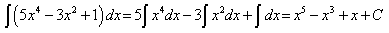 .
.
Пример 4 .
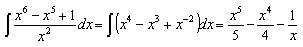 +C
+C
Замена переменной .
Пусть требуется найти неопределенный интеграл 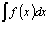 . Сделаем замену в подынтегральном выражении, положив
. Сделаем замену в подынтегральном выражении, положив 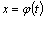 , где
, где 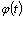 — монотонная непрерывная функция, которая имеет непрерывную производную. Тогда
— монотонная непрерывная функция, которая имеет непрерывную производную. Тогда 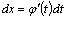 . В этом случае имеет следующее равенство:
. В этом случае имеет следующее равенство:
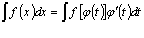
Этот способ часто бывает полезным в тех случаях, когда интеграл не может быть непосредственно преобразован к форме табличного интеграла.
Пример 5
Интеграл 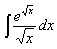 найдем
найдем
подстановкой 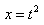 . Тогда:
. Тогда:
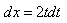
и 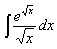 =2
=2 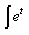 dt=2et +C=2
dt=2et +C=2 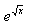 +C.
+C.
Во многих случаях нет необходимости записывать, какое выражение мы принимаем за новую переменную. Вычисления удобно располагать так, какуказано в следующихпримерах.
Пример 6
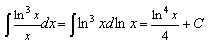 .
.
Пример 7
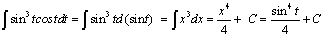 .
.
Пример 8
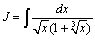 , сделаем замену x = t6, тогда
, сделаем замену x = t6, тогда
Метод интегрирования по частям
Метод интегрирование по частям основан на следующей формуле:
∫udv=uv-∫vdu
где u(x),v(x) –непрерывно дифференцируемые функции. Формула называется формулой интегрирования по частям. Данная формула показывает, что интеграл ∫udv приводит к интегралу ∫vdu, который может оказаться более простым, чем исходный, или даже табличным.
Пример 1. Найти неопределенный интеграл ∫xe-2xdx
Воспользуемся методом интегрирование по частям. Положим u=x, dv=e-2xdx. Тогда du=dx, v=∫xe-2xdx=- 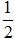 e-2x+C
e-2x+C
Следовательно по формуле имеем:
∫xe-2xdx=x(- 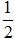 e-2x)-∫-
e-2x)-∫- 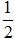 -2dx=-
-2dx=- 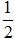 e-2x-
e-2x-  e-2x+C
e-2x+C
Пример 2. ∫(x2+2x)cos2xdx
u=x2+2x, du=(2x+2)dx, dv=cos2xdx, v=∫cos2xdx= 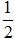 sin2x
sin2x
∫(x2+2x)cos2xdx= 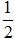 (x2+2x)sin2x-∫(x+1)sin2xdx
(x2+2x)sin2x-∫(x+1)sin2xdx
u=x+1, du=dx, dv=sin2xdx, v=- 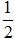 cos2x
cos2x
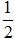 (x2+2x)sin2x-∫(x+1)sin2xdx=
(x2+2x)sin2x-∫(x+1)sin2xdx= 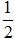 (x2+2x)sin2x+
(x2+2x)sin2x+ 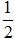 (x+1)cos2x+
(x+1)cos2x+  sin2x+C
sin2x+C
4.Самостоятельное выполнение заданий.
Вариант 1
Найти неопределенные интегралы методом непосредственного интегрирования (для № 1-5).
1. 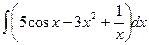 .
.
2. 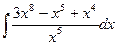 .
.
3. 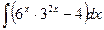 .
.
4. 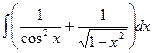 .
.
5. 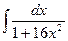 .
.
Найти неопределенные интегралы методом подстановки (для № 6-8).
6. 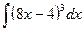 .
.
7. 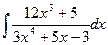 .
.
8. 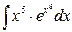 .
.
9. Найти неопределенный интеграл методом интегрирования по частям: 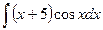 .
.








