Тема 4. Умозаключение как форма мышления
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ»
СПЕЦИАЛИЗИРОВАННЫЙ ФАКУЛЬТЕТ
КАФЕДРА безопасности личности, общества, государства
Дисциплина ЛОГИКА
УТВЕРЖДАЮ
Заведующий кафедрой безопасности личности, общества, государства ___________________ “___”___________2021г.
ФОНДОВАЯ ЛЕКЦИЯ
ТЕМА № 4 УМОЗАКЛЮЧЕНИЕ КАК ФОРМА МЫШЛЕНИЯ
Обсуждено и обговорено
на заседании кафедры
безопасности личности,
общества, государства
Протокол № от 2021
ДОНЕЦК – 2021
Тема 4. Умозаключение как форма мышления
1. Что такое умозаключение?
2. Виды умозаключений.
3. Структура простого силлогизма. Модусы простого силлогизма.
4. Правила терминов простого силлогизма.
5. Правила посылок простого силлогизма.
Понятие, как мы уже знаем, является мысленным обозначением (отражением) какого-либо объекта или его признака, суждение представляет собой некое утвердительное или отрицательное высказывание об объектах, признаках, отношениях и т. п. Умозаключение – это третья (после понятия и суждения) форма мышления, в которой из двух или нескольких суждений, называемых посылками, вытекает новое суждение, называемое заключением, или выводом. В логике принято располагать посылки и вывод друг под другом и отделять посылки от вывода чертой:
Все живые организмы питаются влагой.
Все растения – это живые организмы.
______________________________
Все растения питаются влагой.
В приведенном примере первые два суждения являются посылками, а третье – выводом. Понятно, что посылки должны быть истинными суждениями и должны быть связаны между собой. Если хотя бы одна из посылок ложна, то и вывод ложен:
Все птицы – это млекопитающие животные
Все птицы – это млекопитающие животные.
_________________________________________
Все воробьи – это млекопитающие животные.
Как видим, в приведенном примере ложность первой посылки приводит к ложному выводу, несмотря на то, что вторая посылка является истинной. Если посылки между собой не связаны, то вывод из них сделать невозможно. А
Например, из следующих двух посылок никакого вывода не следует:
Все планеты – это небесные тела
Все сосны являются деревья
__________________________
???
Обратим внимание на то, что умозаключения состоят из суждений, а суждения – из понятий, т.е. одна форма мышления входит в другую в качестве составной части.
Все умозаключения делятся на непосредственные и опосредованные. В непосредственных умозаключениях вывод делается из одной посылки.
Например:
Все цветы являются растениями
____________________________
Некоторые растения являются цветами
Нетрудно догадаться, что непосредственные умозаключения представляют собой уже известные нам операции преобразования простых суждений и выводы об истинности простых суждений по логическому квадрату. Приведенный выше пример непосредственного умозаключения является преобразованием простого суждения путем обращения
В опосредованных умозаключениях вывод делается из нескольких посылок. Например
Все рыбы – это живые существа
Все караси – это рыбы
_______________________
Все караси – это живые существа.
Поскольку непосредственные умозаключения представляют собой различные логические операции с суждениями, то под умозаключениями подразумеваются, прежде всего, опосредованные умозаключения. В дальнейшем речь пойдет именно о них.
2. Виды умозаключений
Умозаключения, или опосредованные умозаключения делятся на три вида. Они бывают дедуктивными, индуктивными и умозаключениями по аналогии.
Дедуктивные умозаключения или дедукция (от лат.deductio – выведение) – это умозаключения, в которых из общего правила делается вывод для частного случая (из общего правила выводится частный случай).
Например:
Все звезды излучают энергию.
Солнце – это звезда
________________________
Солнце излучает энергию.
Как видим, первая посылка представляет собой общее правило, из которого (при помощи второй посылки) вытекает частный случай в виде вывода: если все звезды излучают энергию, значит, Солнце тоже ее излучает, потому что оно является звездой. В дедукции рассуждение идет от общего к частному, от большего к меньшему, знание сужается, в силу чего дедуктивные выводы достоверны, т.е. точны, обязательны, необходимы и т.п. Посмотрим еще раз на приведенный выше пример. Мог бы из двух данных посылок вытекать иной вывод, кроме того, который из них вытекает? Не мог! Вытекающий вывод – единственно возможный в этом случае. Изобразим отношения между понятиями, из которых состояло наше умозаключение, кругами Эйлера. Объемы трех понятий: звезды; тела, излучающие энергию; Солнце схематично расположатся следующим образом:

Несомненное достоинство дедукции, конечно же, заключается в достоверности ее выводов. Вспомним, известный литературный герой Шерлок Холмс пользовался дедуктивным методом при раскрытии преступлений. Это значит, что он строил свои рассуждения таким образом, чтобы из общего выводить частное. В одном произведении, объясняя доктору Ватсону сущность своего дедуктивного метода, он приводит такой пример. Около убитого полковника Морена сыщики Скотланд-Ярда обнаружили выкуренную сигару и решили, что полковник выкурил ее перед смертью. Однако, он (Шерлок Холмс) неопровержимо доказывает, что полковник Морен не мог выкурить эту сигару, потому что он носил большие, пышные усы, а сигара выкурена до конца, т.е., если бы ее курил Морен, то он непременно подпалил бы свои усы. Следовательно, сигару выкурил другой человек. В этом рассуждении вывод выглядит убедительно именно потому, что он дедуктивный: из общего правила (Любой человек с большими, пышными усами не может выкурить сигару до конца) выводится частный случай (Полковник Морен не мог выкурить сигару до конца, потому что носил такие усы). Приведем рассмотренное рассуждение к принятой в логике стандартной форме записи умозаключений в виде посылок и вывода:
1 посылка. Любой человек с большими пышными усами не может выкурить сигару до конца.
2 посылка. Полковник Морен носил большие, пышные усы.
________________________________________________
Умозаключение. Полковник Морен не мог выкурить сигару до конца
Индуктивные умозаключения или индукция (от лат.inductio – наведение) – это умозаключения, в которых из нескольких частных случаев выводится общее правило (несколько частных случаев как бы наводят на общее правило). Например:
Юпитер движется.
Марс движется.
Венера движется.
. 
Все планеты движутся.
Как видим, первые три посылки представляют собой частные случаи, четвертая посылка подводит их под один класс объектов, объединяет их, а в выводе говорится обо всех объектах этого класса, т.е. формулируется некое общее правило (вытекающее из трех частных случаев). Легко увидеть, что индуктивные умозаключения строятся по принципу, противоположному принципу построения дедуктивных умозаключений. В индукции рассуждение идет от частного к общему, от меньшего к большему, знание расширяется, в силу чего индуктивные выводы, в отличие от дедуктивных, не достоверны, а вероятностны. В рассмотренном выше примере индукции признак, обнаруженный у некоторых объектов какой-то группы, перенесен на все объекты этой группы, сделано обобщение, которое почти всегда чревато ошибкой: вполне возможно наличие в группе каких-то исключений, и даже если множество объектов из некой группы характеризуется каким-то признаком, то это не означает с достоверностью, что таким признаком характеризуются все объекты данной группы. Вероятностный характер выводов является, конечно же, недостатком индукции. Однако, ее несомненное достоинство и выгодное отличие от дедукции, которая представляет собой сужающееся знание, заключается в том, что индукция – это расширяющееся знание, способное приводить к новому, в то время как дедукция – это разбор старого и уже известного.
Умозаключения по аналогии или просто аналогия (от греч.analogia – соответствие) – это умозаключения, в которых на основе сходства предметов (объектов) в одних признаках делается вывод об их сходстве и в других признаках. Например:
Планета Земля расположена в солнечной системе, на ней есть атмосфера, вода и жизнь.
Планета Марс расположена в Солнечной системе, на ней есть атмосфера и вода.
Вероятно, на Марсе есть жизнь
Как видим, сравниваются (сопоставляются) два объекта (планета Земля и планета Марс), которые сходны между собой в некоторых существенных, важных признаках (находиться в солнечной системе, иметь атмосферу и воду). На основе данного сходства делается вывод о том, что, возможно, эти объекты сходны между собой и в других признаках: если на Земле есть жизнь, а Марс во многом похож на Землю, то не исключено наличие жизни и на Марсе. Выводы аналогии, как и выводы индукции, вероятностны.
3. Структура простого силлогизма)
Рассмотренные в предыдущем параграфе дедуктивные умозаключения также называются силлогизмами. Существует несколько видов силлогизмов. Первый из них называется простым, или категорическим, потому что все суждения, входящие в него (две посылки и вывод), являются простыми, или категорическими. Это уже известные нам суждения видов А, I, Е, О.
Рассмотрим пример простого силлогизма.
Все цветы (М) – это растения (Р).
Все розы (S) – это цветы (М).
Все розы (S) – это растения(Р).
Обе посылки и вывод являются в данном силлогизме простыми суждениями (причем и посылки, и вывод – это суждения вида А (общеутвердительные)). Обратим внимание на вывод, представленный суждением: Все розы – это растения. В этом выводе субъектом выступает термин розы, а предикатом – термин растения. Субъект вывода присутствует во второй посылке силлогизма, а предикат вывода – в первой. Также в обеих посылках повторяется термин цветы, который, как нетрудно увидеть, является связующим: именно благодаря ему не связанные, разобщенные в посылках термины растения и розы возможно связать в выводе. Таким образом, структура силлогизма включает в себя две посылки и один вывод, которые состоят из трех (различным образом расположенных) терминов.
1. Субъект вывода располагается во второй посылке силлогизма и называется меньшим термином силлогизма (вторая посылка также называется меньшей).
2. Предикат вывода располагается в первой посылке силлогизма и называется большим термином силлогизма (первая посылка также называется большей). Предикат вывода, как правило, является по объему большим понятием, чем субъект вывода (в приведенном примере понятия розы и растения находятся в отношении родо-видового подчинения), в силу чего предикат вывода назван большим термином, а субъект вывода – меньшим.
3. Термин, который повторяется в двух посылках и связывает субъект с предикатом (меньший и больший термины), называется средним термином силлогизма и обозначается латинской буквой М, потому что «средний» на латинском – это medium.
Три термина силлогизма могут быть расположены в нем по-разному. Взаимное расположение терминов друг относительно друга называется фигурой простого силлогизма. Таких фигур четыре, т.е. все возможные варианты взаимного расположения терминов в силлогизме исчерпываются четырьмя комбинациями. Рассмотрим их.
Первая фигура силлогизма – это такое расположение его терминов, при котором первая посылка начинается со среднего термина, а вторая заканчивается средним термином. Например:
Все газы ( M ) – это химические элементы ( P )
Гелий ( S ) – это газ ( M )/
________________________________
Гелий ( S ) – это химический элемент ( P )
Учитывая то, что в первой посылке средний термин связан с предикатом, во второй субъект связан со средним термином, а в выводе субъект связан с предикатом, составим схему расположения и связи терминов в приведенном примере:

Прямые линии на схеме (за исключением той, которая отделяет посылки от вывода) показывают связь терминов в посылках и в выводе. Поскольку роль среднего термина заключается в том, чтобы связывать больший и меньший термины силлогизма, то на схеме средний термин в первой посылке соединяется линией со средним термином во второй посылке. Схема показывает, каким именно образом средний термин связывает между собой другие термины силлогизма в его первой фигуре. Кроме того, можно изобразить отношения между тремя терминами с помощью кругов Эйлера. В данном случае получится следующая схема:
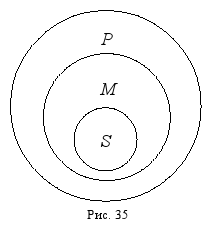
2. Вторая фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки заканчиваются средним термином.
Например:
Все рыбы ( P ) дышат жабрами ( M )
Все киты ( S ) не дышат жабрами ( M )
_______________________________
Все киты ( S ) не рыбы ( P )
Схемы взаимного расположения терминов и отношений между ними во второй фигуре силлогизма выглядят так:

Третья фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки начинаются со среднего термина. Например:
Все тигры (М) – это млекопитающие (Р).
Все тигры (М) – это хищники (S).
_____________________________________
Некоторые хищники (S) – это млекопитающие (Р).
Схемы взаимного расположения терминов и отношений между ними в третьей фигуре силлогизма (рис. 37):

4. Четвертая фигура силлогизма – это такое расположение его терминов, при котором первая посылка заканчивается средним термином, а вторая начинается с него. Например:
Все квадраты (Р) – это прямоугольники (М).
Все прямоугольники (М) – это не треугольники (S).
____________________________________________
Все треугольники (S) – это не квадраты (Р).
Схемы взаимного расположения терминов и отношений между ними в четвёртой фигуре силлогизма (рис. 38):

Отметим, что отношения между терминами силлогизма во всех фигурах могут быть и другими.
Модусы простого силоогизма
Любой простой силлогизм состоит из трех суждений (двух посылок и вывода). Каждое из них является простым и принадлежит к одному из четырех видов (А, I, Е, О). Набор простых суждений, входящих в силлогизм, называется модусом простого силлогизма.
Например:
Все небесные тела движутся.
Все планеты – это небесные тела.
__________________________________
Все планеты движутся.
В силлогизме первая посылка является простым суждением вида A (общеутвердительным), вторая посылка – это тоже простое суждение вида A, и вывод в данном случае представляет собой простое суждение вида A. Поэтому рассмотренный силлогизм имеет модус AАA.
Во втором примере:
Все журналы – это периодические издания.
Все книги не являются периодическими изданиями.
____________________________________________
Все книги не являются журналами.
Силлогизм имеет модус AEE.
В третьем примере:
Все углероды – простые тела.
Все углероды электропроводны.
______________________________________
Некоторые электропроводники – простые тела.
Силлогизм имеет модус AAI.
Всего модусов во всех четырёх фигурах, т. е. возможных комбинаций простых суждений в силлогизме, – 256. В каждой фигуре 64 модуса. Однако из этих 256 модусов только 19 дают достоверные выводы, остальные приводят к вероятностным выводам. Если принять во внимание, что одним из главных признаков дедукции (а значит, и силлогизма) является достоверность её выводов, то становится понятным, почему эти 19 модусов называются правильными, а остальные – неправильными.
Наша задача – уметь определять фигуру и модус любого простого силлогизма. Например, требуется установить фигуру и модус силлогизма:
Все вещества состоят из атомов.
Все жидкости – это вещества.
_______________________________
Все жидкости состоят из атомов.
Прежде всего надо найти субъект и предикат вывода, т. е. меньший и больший термины силлогизма. Далее следует установить местоположение меньшего термина во второй посылке и большего – в первой. После этого можно определить средний термин и схематично изобразить расположение всех терминов в силлогизме (рис. 39):
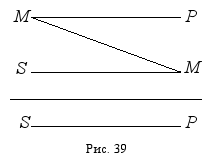
Все вещества (М) состоят из атомов (Р).
Все жидкости (S) – это вещества (М).
________________________________
Все жидкости (S) состоят из атомов (Р).
Как видим, рассматриваемый силлогизм построен по первой фигуре. Теперь надо найти его модус. Для этого следует выяснить, к какому виду простых суждений относятся первая и вторая посылки и вывод. В нашем примере обе посылки и вывод являются суждениями вида A (общеутвердительными), т. е. модус данного силлогизма – AАA. Итак, предложенный силлогизм имеет первую фигуру и модус AАA.
Вывод простого силлогизма является истинным, конечно же, в том случае, когда истинны его посылки. Однако, истинность посылок – это не достаточное условие истинности вывода. Вполне может быть так, что обе посылки в силлогизме истинны, а вывод его ложен. Например:
Все дети обладают мышлением.
Все взрослые – это не дети
 Все взрослые не обладают мышлением.
Все взрослые не обладают мышлением.
В этом силлогизме, построенном по первой фигуре, и имеющим модус АЕЕ, и первая, и вторая посылки являются истинными суждениями, из которых вытекает ложный вывод. Почему так получается? Потому что при построении силлогизма следует обращать внимание не только на то, чтобы посылки были истинными, но и, в не меньшей степени, на то, чтобы были соблюдены определенные требования или правила его построения. Рассмотрим еще один пример:
Все нравственные заповеди надо соблюдать.
Законы государства не являются нравственными заповедями.
___________________________________
Законы государства не надо соблюдать
Данный силлогизм также построен по первой фигуре и имеет модус АЕЕ. В нем из истинных посылок вытекает ложный вывод из-за нарушения правил простого силлогизма, которые будут рассмотрены далее.
4. Правила терминов простого силлогизма
Правила простого силлогизма делятся на общие и частные. Общие правила применимы ко всем простым силлогизмам, независимо от того, по какой фигуре они построены. Частные правила действуют только для каждой фигуры силлогизма и поэтому часто называются правилами фигур. Вспомним, что в структуре простого силлогизма выделяются три термина (больший, меньший и средний) и две посылки (большая и меньшая). Поэтому общие правила простого силлогизма обычно делятся на правила терминов и правила посылок силлогизма. Сначала рассмотрим правила терминов.
1. В силлогизме должно быть только три термина. Обратимся к уже упоминавшемуся (см.введение) примеру силлогизма, в котором данное правило нарушено:
Движение вечно.
Хождение в школу – это движение.
Хождение в школу вечно
Обе посылки этого силлогизма являются истинными суждениями, однако из них вытекает ложный вывод, потому что нарушено рассматриваемое правило. Термин движение употребляется в двух посылках в двух разных смыслах (движение как всеобщее мировое изменение и движение как механическое перемещение тела из точки в точку), и получается, что терминов в силлогизме три (движение, хождение в школу, вечность), а смыслов (поскольку один из терминов употребляется в двух разных смыслах) четыре, т.е. лишний смысл как бы подразумевает лишний термин. Иначе говоря, в приведенном примере силлогизма было не три, а четыре (по смыслу) термина. Ошибка, возникающая при нарушении вышеприведенного правила, называется учетверением терминов.
2. Средний термин должен быть распределен хотя бы в одной из посылок. О распределенности терминов в простых суждениях речь шла в предыдущей главе. Напомним, что проще всего устанавливать распределенность терминов в простых суждениях с помощью круговых схем: надо изобразить кругами Эйлера отношения между терминами суждения, при этом полный круг на схеме будет обозначать распределенный термин (+), а неполный – нераспределенный (-). Рассмотрим пример силлогизма:
Все кошки – это живые существа.
Сократ – это тоже живое существо
__________________
Сократ – это кошка.
Из двух истинных посылок вытекает ложный вывод. Изобразим кругами Эйлера отношения между терминами в посылках силлогизма и установим распределенность этих терминов:

Как видим, средний термин (живые существа) в данном случае нераспределен ни в одной из посылок, а по правилу он должен быть распределен хотя бы в одной из посылок. Ошибка, возникающая при нарушении рассматриваемого правила, так и называется – нераспределенность среднего термина в каждой посылке.
3. Термин, который был нераспределен в посылке, не может быть распределен в выводе. Обратимся к следующему примеру:
Все яблоки – съедобны.
Все груши – это не яблоки
Все груши несъедобны
Посылки силлогизма являются истинными суждениями, а вывод – ложным. Как и в предыдущем случае, изобразим кругами Эйлера отношения между терминами в посылках и в выводе силлогизма и установим распределенность этих терминов:
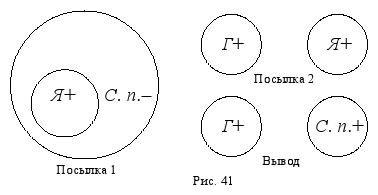
В данном случае предикат вывода, или больший термин силлогизма (съедобные предметы) в первой посылке является нераспределенным (-), а в выводе – распределенным (+), что запрещается рассматриваемым правилом. Ошибка, возникающая при его нарушении, называется расширением большего термина. (Вспомним, что термин распределен, когда речь идет обо всех предметах, входящих в него и нераспределен, когда речь идет о части предметов, входящих в него, именно поэтому ошибка и называется расширением термина).
Таковы правила терминов простого силлогизма. Теперь перейдем к рассмотрению правил его посылок.
5. Правила посылок простого силлогизма.
1. В силлогизме не должно быть двух отрицательных посылок. Хотя бы одна из посылок силлогизма должна быть положительной (могут быть положительными и обе посылки). Если две посылки в силлогизме отрицательные, то вывод из них или вообще сделать нельзя, или же, если его сделать возможно, он будет ложным или, по крайней мере, недостоверным, вероятностным. Например:
Снайперы не могут иметь плохое зрение.
Все мои друзья – не снайперы.
_______________________________
Все мои друзья имеют плохое зрение.
Обе посылки в силлогизме являются отрицательными суждениями, и, несмотря на их истинность, из них вытекает ложный вывод.
Ошибка, которая возникает в данном случае, так и называется – две отрицательные посылки.
2. В силлогизме не должно быть двух частных посылок. Хотя бы одна из посылок должна быть общей (могут быть общими и обе посылки). Если две посылки в силлогизме представляют собой частные суждения, то вывод из них сделать невозможно. Например:
Некоторые школьники – это первоклассники.
Некоторые школьники – это десятиклассники.
???
Из этих посылок никакой вывод не следует, потому что обе они являются частными. Ошибка, возникающая при нарушении данного правила, так и называется – две частные посылки.
3. Если одна из посылок отрицательная, то и вывод должен быть отрицательным. Например:
Ни один металл не является изолятором.
Медь – это металл.
_______________________________
Медь не является изолятором.
Как видим, из двух посылок данного силлогизма не может вытекать утвердительный вывод. Он может быть только отрицательным.
4. Если одна из посылок частная, то и вывод должен быть частным. Например:
Все углеводороды – это органические соединения.
Некоторые вещества – это углеводороды.
____________________________________
Некоторые вещества – это органические соединения.
В этом силлогизме из двух посылок не может следовать общий вывод. Он может быть только частным, т. к. вторая посылка является частной.








