Вопросы к зачету по курсу

Дата: 2025-05-25; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

«Обыкновенные дифференциальные уравнения», весенний семестр, 2014/15 уч.год.

 

На тройку.

1. Определения:

Фазовое пространство, фазовая траектория;
решение диф.уравнения, общее решение, частное решение, интегральная кривая;
фундаментальная матрица для линейной системы,
основная матрица фундаментальной матрицы для периодической системы;
постановка задачи Коши для одного уравнения n-го порядка, для системы n уравнений 1-го порядка;
устойчивость по Ляпунову и асимптотическая устойчивость;
линеаризация;
разностная схема;
аппроксимация задачи с помощью разностной схемы;
устойчивость разностной схемы.

 

2. Теоремы и свойства (без доказательств):
теорема о существовании и единственности решения задачи Коши для общей системы и для линейной системы;
структура общего решения линейной однородной и неоднородной систем;
связь свойств основной матрицы с устойчивостью линейной периодической системы;
непрерывная зависимость от параметра и дифференцируемость по параметру решения задачи Коши;
теорема об устойчивости по первому приближению;
теорема о сходимости разностной схемы.

3. Практика:
Определить, к какому из трех типов относится данное уравнение 1-го порядка (с разд
переменными, однородное, линейное) и найти его общее решение;
Найти фундаментальную матрицу для данного линейного уравнения 2-го порядка с постоянными коэффициентами.

Больше, чем на тройку – все, что на тройку, и уметь кое-что доказывать.

Вопросы для самоконтроля.

 

  1. Приведите примеры метрических пространств.
  2. Какое отображение называется сжимающим?
  3. Фазовая траектория и интегральная кривая - геометрические образы решений дифференциального уравнения.
    Чем они отличаются друг от друга?
  4. Могут ли интегральные кривые пересекаться? А самопересекаться? Тот же вопрос для фазовыхтраекторий.
  5. Какое свойство правой части дифференциального уравнения делает соответствующий интегральный оператора сжимающим?
  6. Линейная система – частный случай общей системы. Зачем для нее доказывать отдельно теорему существования?
  7. Любое решение некоторой линейной однородной системы с постоянными коэффициентами стремится к 0 при 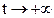. Что можно сказать о собственных числах матрицы этой системы?
  8. Какому условию должны удовлетворять характеристические показатели линейной однородной системы с периодическими коэффициентами, чтобы существовало периодическое решение этой системы?
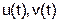  9. - решения уравнения 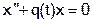, причем . Вычислите вронскиан этих решений, (см. формулу Лиувилля).
  10. В чем существенное отличие уравнения Бесселя от уравнений, для которых доказывалась теорема существования и единственности решения задачи Коши ?
  11. Пусть коэффициенты уравнения 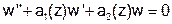аналитичны в области D. Следует ли отсюда, что любое решение задачи Коши также будет аналитично в этой области?
  12. Как связаны порядок аппроксимации и скорость сходимости разностной схемы ?