Эвольвентных передач на выносливость
4.1.12. Определяют по формулам табл. 4.6 силы, действующие в зацеплении. В приведенных формулах: Ft, Fr, Fx в Н; Т1, Т2 в Н·м; dw в мм; Р в кВт; v в м/с; αw = 20° (при xΣ = 0); значение αtw при xΣ ≠ 0, см. в литературе [12, с. 24-25; 19, с. 244].
Таблица 4.6
| Сила | Виды передач | |
| Прямозубая | Косозубая или шевронная | |
| Окружная Ft |
| |
| Радиальная Fr | 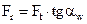
| 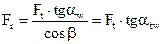
|
| Осевая Fx | – | 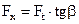
|
Примечание. У шевронной передачи или передачи с раздвоенной ступенью усилия, возникающие на каждом из полушевронов, составляют половину расчетного усилия; осевые силы равны по величине, но направлены в противоположные стороны и их результирующая равна нулю. Это условие соблюдается, если один из валов передачи выполнен «плавающим».
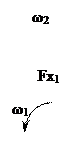
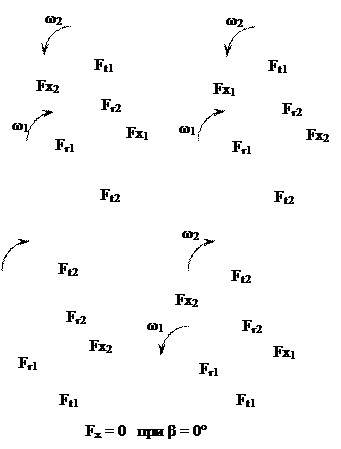
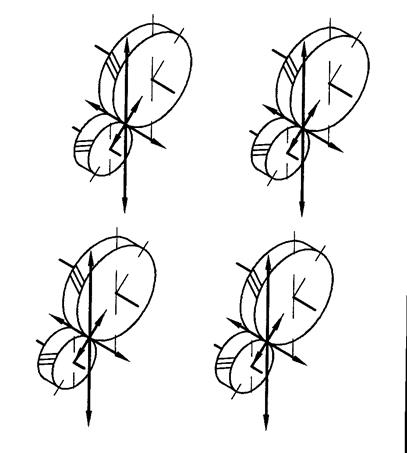
Рис. 4.4. Силы, действующие в зацеплении
цилиндрических зубчатых передач
Эскиз, отражающий положение зубчатых колес в пространстве и направление действующих сил, помещают в пояснительную записку. Эта информация используется при расчете валов и подборе подшипников.
4.2. Проверочный расчет
После определения основных параметров передачи выполняют проверочный расчет на контактную выносливость рабочих поверхностей зубьев. При сопоставлении расчетного контактного напряжения σН (МПа) и допускаемого σНР должно соблюдаться условие
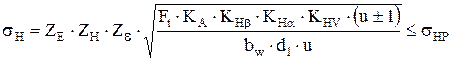 , (4.9)
, (4.9)
где ZE – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес;
ZН – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления;
Zε – коэффициент, учитывающий суммарную длину контактных линий;
КА – коэффициент, учитывающий внешнюю динамическую нагрузку;
КНβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;
КНα – коэффициент, учитывающий распределение нагрузки между зубьями;
КНv – коэффициент, учитывающий динамическую нагрузку, действующую в зацеплении до зоны резонанса;
Ft – окружная сила, Н;
bw – рабочая ширина венца, мм;
d1 – делительный диаметр шестерни, мм;
u – передаточное число передачи.
4.2.1. Коэффициент ZE определяют по формуле
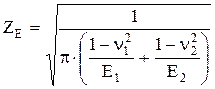 ,
,
где Е1, Е2 – модули упругости материала зубчатых колес, МПа;
n1, n2 – коэффициенты Пуассона [27, с. 121].
Для зубчатой передачи со стальными зубчатыми колесами ZE = 190.
4.2.2. Коэффициент ZН принимают по рис. 4.5 в зависимости от отношения 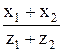 ,
,
где x1 и x2 – соответственно коэффициенты смещения исходного контура; для несмещенных передач x1 = x2 = 0;
z1 и z2 – числа зубьев зубчатых колес.
4.2.3. Коэффициент Zε определяют с учетом коэффициентов осевого εβ и торцового перекрытия εα по формулам [14; 20, с. 45-46] или графикам (рис. 4.6).
|
|
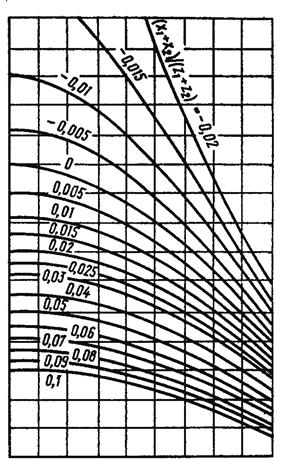
Рис. 4.5. График для определения
коэффициента ZН
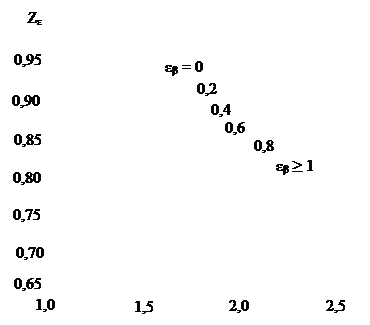 |
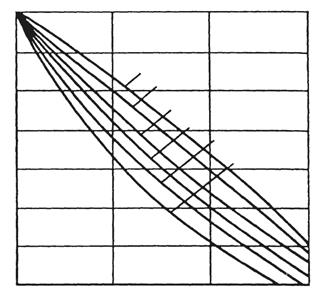
Рис. 4.6. График для определения коэффициента zε
Коэффициенты осевого εβ и торцового перекрытия εα определяют из выражений
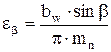 , (4.10)
, (4.10)
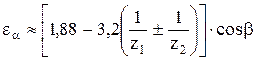 , (4.11)
, (4.11)
где bw – рабочая ширина венца, мм;
β – угол наклона линии зуба, град. (п. 4.1.8);
mn – нормальный модуль, мм.
Для смещенных передач вместо приближенной формулы (4.11) рекомендуется использовать зависимости, приведенные в ГОСТ 21354-87 [14, с. 111-112].
4.2.4. Коэффициент КА = 1, если в циклограмме нагружения учтены все внешние нагрузки. В противном случае используют рекомендации ГОСТ 21354-87 [14, с. 67-70].
4.2.5. Коэффициент КНβ определяется по рис. 4.1.
4.2.6. Для прямозубых передач КНα = 1. Для колес с непрямыми зубьями КНα приближенно может быть найден по рис. 4.7. Более точные значения обеспечивают формулы, приведенные в ГОСТ 21354-87 [14, с.18-19,116].

|
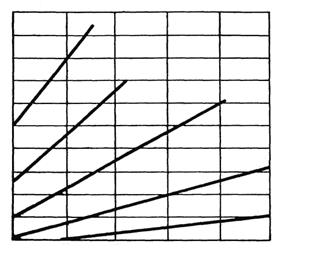
Рис. 4.7. График для определения коэффициента КНα для косозубых
и шевронных передач (цифры у кривых обозначают степени точности
по нормам плавности работы)
4.2.7. Коэффициент КНv определяют по формуле
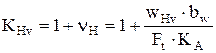 , (4.12)
, (4.12)
если выполнены условия:
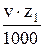 < 1 для прямозубых передач (4.13)
< 1 для прямозубых передач (4.13)
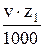 < 1,4 для передач с непрямыми зубьями. (4.14)
< 1,4 для передач с непрямыми зубьями. (4.14)
При невыполнении условий (4.13) и (4.14) КНv определяют по формулам, приведенным в ГОСТ 21354-87 [14, с.70-73].
В зависимостях (4.12)-(4.14):
nН – динамическая добавка;
wHv – удельная окружная динамическая сила, Н/мм;
bw – рабочая ширина венца, мм;
Ft – окружная сила, Н;
v – окружная скорость, м/с;
z1 – число зубьев шестерни;
КА – коэффициент, учитывающий внешнюю динамическую нагрузку (см. п. 4.2.4).
Удельная окружная динамическая сила, Н/мм, определяется по формуле
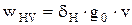
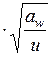 , (4.15)
, (4.15)
где v – м/с, aw – мм.
Входящий в формулу (4.15) коэффициент δН, учитывающий влияние проявления погрешностей зацепления на динамическую нагрузку, находят по табл. 4.7, а коэффициент g0, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса, – по табл. 4.8. Если значения wHv, вычисленные по формуле (4.15), превышают предельные значения, указанные в табл. 4.9, то их следует принимать равными этим значениям.
Таблица 4.7
| Твердость поверхностей зубьев по Виккерсу | Вид зубьев | δН |
| Н1≤ 350 HV или Н2≤ 350 HV | Прямые без модификации головки Прямые с модификацией головки Косые | 0,06 0,04 0,02 |
| Н1> 350 HV Н2> 350 HV | Прямые без модификации головки Прямые с модификацией головки Косые | 0,14 0,10 0,04 |
Таблица 4.8
| Модуль m, мм | Значение g0 | |||||
| Степень точности по нормам плавности | ||||||
| 5 | 6 | 7 | 8 | 9 | 10 | |
| До 3,55 Св. 3,55 до 10 Св. 10 | 2,8 3,1 3,7 | 3,8 4,2 4,8 | 4,7 5,3 6,4 | 5,6 6,1 7,3 | 7,3 8,2 10,0 | 10,0 11,0 13,5 |
Таблица 4.9
| Модуль m, мм | Предельные значения wHv, wFv, Н/мм | |||||
| Степень точности по нормам плавности работы | ||||||
| 5 | 6 | 7 | 8 | 9 | 10 | |
| До 3,55 Св. 3,55 до 10 Св. 10 | 85 105 150 | 160 194 250 | 240 310 450 | 380 410 590 | 700 880 1050 | 1200 1500 1800 |
4.2.8. Значения Ft, bw, u и d1 принимают из предыдущих расчетов, в том числе пп. 4.1.12, 4.1.9 и др.
4.2.9. После завершения вычислений по формулам (4.15) и (4.12) находят расчетное контактное напряжение σН по формуле (4.9) и сравнивают его с допускаемым σНР, значение которого следует уточнить, если имеются существенные различия между исходными параметрами, на основе которых было найдено σНР и окончательно принятыми.
В тех случаях, когда σН отклоняется от σНР больше чем на ± 5%, можно изменить в небольших пределах рабочую ширину венца bw (увеличив ее при перегрузке передачи и уменьшив при недогрузке). Если эти попытки не приводят к желаемым результатам, то расчет проводят повторно, изменяя и другие параметры, например aw, а также степень точности колес, их материал и режим термообработки с целью изменения значения σНР. В последнем случае резко возрастают затраты времени на перерасчет.
5. РАСЧЕТ АКТИВНЫХ ПОВЕРХНОСТЕЙ ЗУБЬЕВ НА КОНТАКТНУЮ ПРОЧНОСТЬ
Расчет проводят, сопоставляя расчетное напряжение σНmax, МПа, и допускаемое предельное контактное напряжение σНРmax (см. п. 3.2). При этом должно выполняться условие
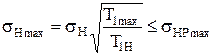 *,
*,
где σН – расчетное контактное напряжение, МПа (см. формулу (4.9));
Т1Н – исходная расчетная нагрузка, Н×м;
Т1max – наибольшая нагрузка из числа подводимых к передаче, Н×м.
Наибольшая нагрузка (наибольший крутящий момент) определяется по циклограмме нагружения или типовому режиму нагружения (рис.3.1). В некоторых случаях ее принимают равной крутящему моменту, создаваемому в передаче при максимальной загрузке двигателя.
6. РАСЧЕТ ЗУБЬЕВ ЦИЛИНДРИЧЕСКИХ
ЭВОЛЬВЕНТНЫХ ПЕРЕДАЧ НА ВЫНОСЛИВОСТЬ
ПРИ ИЗГИБЕ
Для предотвращения усталостного излома зубьев производят сопоставление расчетного напряжения на переходной поверхности зуба σF, МПа, с допускаемым напряжением σFР (см. п. 3.3). При этом должно соблюдаться условие
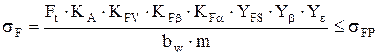 , (6.1)
, (6.1)
где 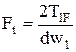 – окружная сила, Н (см. п. 3.3.7 и 4.1.9);
– окружная сила, Н (см. п. 3.3.7 и 4.1.9);
bw – рабочая ширина венца в зубчатой передаче, мм;
m(mn) – нормальный модуль, мм;
КА – коэффициент, учитывающий внешнюю нагрузку;
КFv – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса;
КFβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;
КFa – коэффициент, учитывающий распределение нагрузки между зубьями;
YFS – коэффициент, учитывающий форму зуба и концентрацию напряжений;
Yβ – коэффициент, учитывающий наклон зуба;
Ye – коэффициент, учитывающий перекрытие зубьев.
Расчетом определяют напряжение в опасном сечении на переходной поверхности зуба для каждого зубчатого колеса. При расчетах можно использовать зависимость
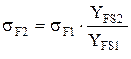 . (6.2)
. (6.2)
6.1. Значения Ft, bw, m(mn) вычисляют или заимствуют из предыдущих расчетов (пп. 3.3.7, 4.1.7, 4.1.9, 4.1.12).
6.2. Коэффициент КА = 1, если в циклограмме нагружения учтены все внешние нагрузки. В противном случае используют рекомендации ГОСТ 21354-87 [14, с. 67-70].
6.3. Коэффициент КFv определяют по формуле
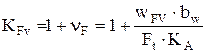 , (6.3)
, (6.3)
если выполнены условия:
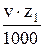 < 1 для прямозубых передач, (6.4)
< 1 для прямозубых передач, (6.4)
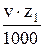 < 1,4 для передач с непрямыми зубьями. (6.5)
< 1,4 для передач с непрямыми зубьями. (6.5)
Обозначения в формулах (6.3) – (6.5) те же, что и в формулах (4.12) – (4.14), за исключением nF – динамической добавки и wFv – удельной окружной динамической силы, Н/мм, которая может быть определена по формуле
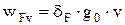
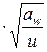 , (6.6)
, (6.6)
где v – м/с, aw – мм.
Входящий в формулу (6.6) коэффициент g0, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса, находят по табл. 4.8. Коэффициент δF, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев, принимают для косозубых и шевронных передач равным 0,06, для прямозубых передач с модификацией головки δF = 0,11, для прямозубых передач без модификации головки δF = 0,16. Если значения wFv, вычисленные по формуле (6.6), превышают предельные значения, указанные в табл. 4.9, то их следует принимать равными этим значениям.
6.4. Коэффициент КFβ определяется по рис. 6.1.
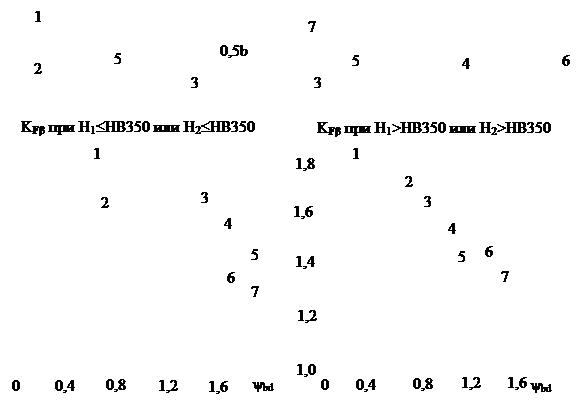 |
|
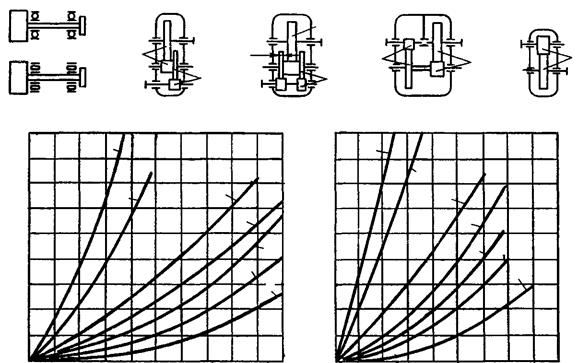
Рис. 6.1. График для определения ориентировочных значений
коэффициента КFβ ( цифры у кривых соответствуют передачам,
указанным на схемах)
6.5. Коэффициент КFa находят, используя те же рекомендации, что и для выбора коэффициента КНa (см. п.4.2.6).
6.6. Коэффициент, учитывающий форму зуба и концентрацию напряжений в передачах внешнего зацепления, находят по рис. 6.2 или вычисляют по формуле
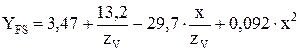 ,
,
где x – коэффициент смещения [12, с. 50-55; 17, с. 172-176].
zv – эквивалентное число зубьев.
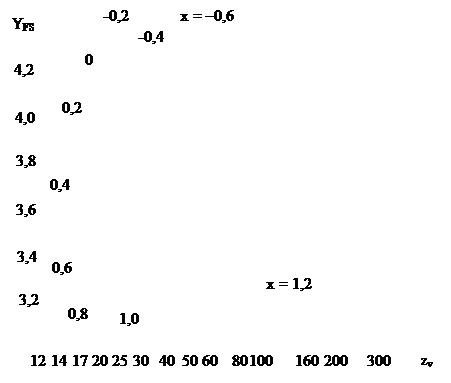
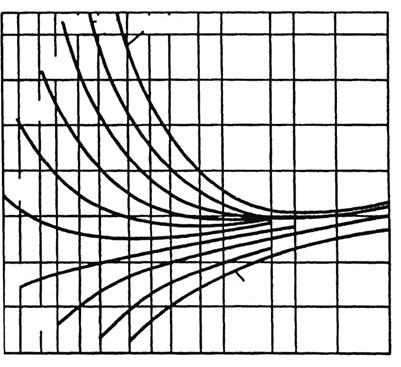
Рис. 6.2. Графики для определения коэффициента YFS
(зубчатые колеса внешнего зацепления)
Эквивалентное число зубьев шестерни или колеса определяют по зависимости 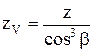 , где β – угол наклона линии зуба, град.
, где β – угол наклона линии зуба, град.
Для колес с внутренними зубьями коэффициент YFS2 можно приближенно определить по формуле 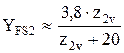 (колеса без смещения). Более точные результаты дают графики рекомендаций [21, с. 13-18], учитывающие величину смещения x и число зубьев долбяка z0. На рис. 6.3, а, б приведены такие графики для прямозубых передач при z0 = 20 и z0 = 30.
(колеса без смещения). Более точные результаты дают графики рекомендаций [21, с. 13-18], учитывающие величину смещения x и число зубьев долбяка z0. На рис. 6.3, а, б приведены такие графики для прямозубых передач при z0 = 20 и z0 = 30.
Примечание. Для внутреннего зацепления коэффициент YFS2 в зависимости от смещения и числа зубьев зубодолбежного инструмента приводится также в справочнике [12, с. 274]. Там же имеются сведения о выборе коэффициентов смещений, основных параметрах долбяков и минимальном числе нарезаемых ими зубьев [12, с. 32-34, 53-55].

|
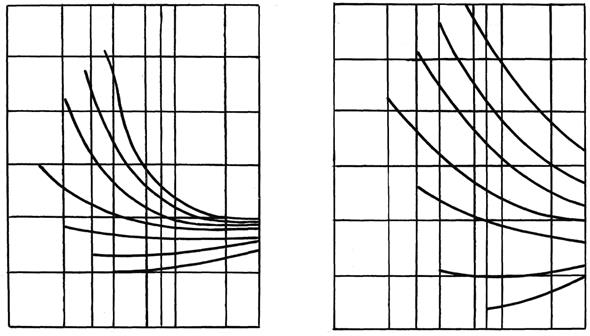
а б
Рис. 6.3. Графики для определения коэффициента YFS2 (прямозубые колеса с внутренними зубьями)
6.7. Коэффициент Yβ, учитывающий наклон зубьев, определяют по формуле
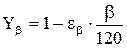 (принимаются только значения Yβ ≥ 0,7),
(принимаются только значения Yβ ≥ 0,7),
где eβ – коэффициент осевого перекрытия (см. формулу (4.10));
β – угол наклона линии зуба, град.
6.8. Коэффициент Ye, учитывающий перекрытие зубьев, для прямозубых передач при предварительных расчетах принимают равным 1 (уточнения см. в ГОСТ 21354-87). Для косозубых передач 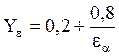 (при εβ < 1) и
(при εβ < 1) и 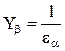 (при εβ ≥ 1). Значения eβ и ea вычисляют по формулам (4.10) и (4.11).
(при εβ ≥ 1). Значения eβ и ea вычисляют по формулам (4.10) и (4.11).
6.9. Определив σF1 по формуле (6.1), находят σF2, используя зависимость (6.2), и сравнивают полученные значения с допускаемыми напряжениями σFР1(2).
6.10. Если значение σF1(2), найденное по формуле (6.1), превысит допускаемое значение σFР1(2) больше чем на 5%, то можно попытаться увеличить ширину зубчатых колес в допустимых пределах (см. табл. 4.1) или увеличить модуль до ближайшего стандартного значения в рекомендуемом интервале и повторить расчет, начиная с п. 4.1.7. При недогрузке передачи, даже значительной, перерасчет можно не производить, т.к. определяющей в этом случае будет контактная, а не изгибная прочность.
*При Т1Н = Т1Нmax вывод о достаточной прочности и выносливости материала основывается на расчетах по п. 4.2, т.к. σН = σНmax и необходимость в расчетах по п. 5 отпадает. Аналогичное положение может возникнуть при расчетах по п. 7.