Задание на самостоятельную работу №3.
Тема: Математическое программирование.
Методические указания по выполнению работы №3.
1. Проработать лекционный материал раздела «Математическое программирование».
2. Решить следующие задачи.
2.1. Привести задачу линейного программирования
f(x) = x1 + x2 – x3 -> max,
2x1 + x2 – x3 + x4 ≤ 1,
x1 + 2x2 - x4 = -2,
x1 + x2 + x3 ≥ 3,
xj ≥ 0, j = 1,…,4
к каноническому виду.
2.2. Изобразить на плоскости множество точек (х1, х2), удовлетворяющих системе неравенств
x1 + x2 ≤ 4,
4x1 + 3x2 ≤ 12,
-x1 + x2 ≥ 1,
x1 + x2 ≤ 6,
x1 ,x2 ≥ 0.
Какое из ограничений является избыточным?
3. Графически решить задачу.
1) 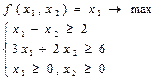
2) 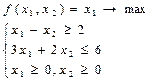
3) 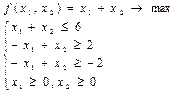
4) 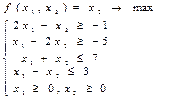
5) 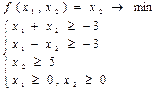
6) 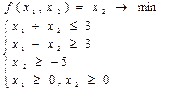
7) 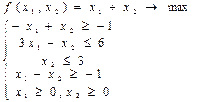
8) 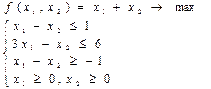
9) 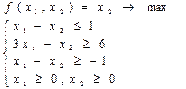
10) 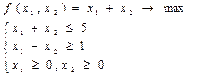
11) 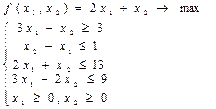
12) 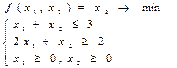
13) 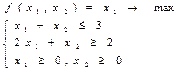
14) 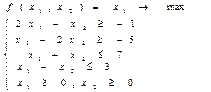
15) 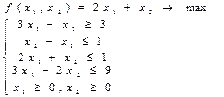
16) 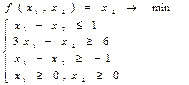
17) 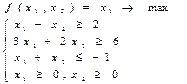
18) 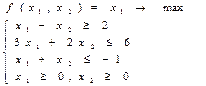
19) 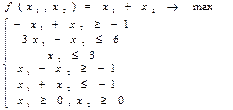
20) 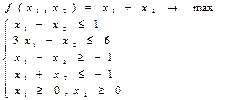
4. Графически решить задачу. Определить следующий шаг при решении основной задачи линейного программирования симплекс методом (в какой точке находимся, ее характеристика, если надо - разрешающий элемент для следующего шага).
1)
| X1 | X2 | -b | |
| Y1 | -1 | 1 | 1 |
| Y2 | 2 | -1 | -3 |
| Y3 | 6 | -1 | 2 |
| Y4 | 3 | 1 | 1 |
| 4 | 2 | 0 |
2)
| Y1 | Y2 | -b | |
| X1 | -1 | 1 | 1 |
| X2 | -2 | -1 | -3 |
| Y3 | 6 | -1 | 2 |
| Y4 | 3 | 1 | 1 |
| 4 | 2 | 0 |
3)
| Y1 | X2 | -b | |
| X1 | -1 | 1 | 1 |
| Y2 | -2 | -1 | 3 |
| Y3 | 6 | -1 | 2 |
| Y4 | 3 | 1 | 1 |
| 4 | 2 | 0 |
4)
| Y1 | Y2 | -b | |
| Y4 | -1 | 1 | 1 |
| X2 | -2 | -1 | 3 |
| Y3 | 6 | -1 | -2 |
| X1 | 3 | 1 | 1 |
| 4 | 2 | 0 |
5)
| Y1 | Y2 | -b | |
| Y4 | -1 | 1 | 1 |
| X2 | -2 | -1 | 3 |
| X1 | 6 | -1 | 2 |
| Y3 | 3 | 1 | 1 |
| -4 | 2 | 0 |
6)
| Y1 | Y2 | -b | |
| Y4 | 1 | 1 | 1 |
| X2 | 2 | -1 | 3 |
| X1 | 6 | -1 | 2 |
| Y3 | 3 | 1 | 1 |
| -4 | 2 | 0 |
7)
| X1 | X2 | -b | |
| Y1 | 1 | 1 | 1 |
| Y2 | 2 | -1 | 3 |
| Y3 | 6 | -1 | 2 |
| Y4 | 3 | 1 | 1 |
| -4 | 2 | 0 |
8)
| Y1 | Y2 | -b | |
| X1 | -1 | 1 | 1 |
| X2 | -2 | 1 | -3 |
| Y3 | 6 | -1 | 2 |
| Y4 | 3 | 1 | 1 |
| 4 | 2 | 0 |
| Y1 | X2 | -b | |
| X1 | -1 | 1 | 1 |
| Y2 | -2 | -1 | 3 |
| Y3 | 6 | -1 | 2 |
| Y4 | 3 | 1 | 1 |
| 4 | 2 | 0 |
9)
10)
| Y1 | Y2 | -b | |
| Y4 | -1 | 1 | 1 |
| X2 | -2 | 1 | 3 |
| Y3 | 6 | 1 | 2 |
| X1 | 3 | 1 | 1 |
| 4 | -2 | 0 |








