Собственно задачи на движение (по количеству выполняемых действий): простые, составные. Простые задачи на движение
Таблица 16
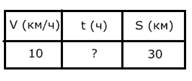
| Основные понятия и обозначения | Форма краткой записи | Применяемые формулы | Средство наглядности |
| Скорость – V Время – t Расстояние (путь) - S | Таблица | 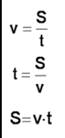
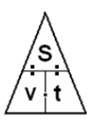
| 
|
Таблица 17
| Велосипедист со скоростью 10 км/ч ехал в течение 3 часов. Какое расстояние он проехал? | Велосипедист за 3 часа проехал 30 км. С какой скоростью он ехал? | Велосипедист со скоростью 10 км/ч проехал 30 км. Сколько времени был в пути велосипедист? |
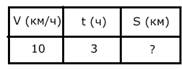 10●3=30 (км)
Ответ: 30 км проехал велосипедист.
10●3=30 (км)
Ответ: 30 км проехал велосипедист.
| 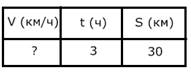 30:3=10 (км/ч)
Ответ: со скоростью 10 км/ч ехал велосипедист.
30:3=10 (км/ч)
Ответ: со скоростью 10 км/ч ехал велосипедист.
|  30:10=3 (ч)
Ответ: 3 часа был в пути велосипедист.
30:10=3 (ч)
Ответ: 3 часа был в пути велосипедист.
|
Составные задачи на движение подразделяются:
1) по типу связей между данными и искомым:
Таблица 18
| № | Виды задач | Форма краткой записи | Основа способа решения | Примеры задач |
| 1 | Нахождение четвертого пропорционального | таблица | нахождение значения постоянной величины
| Теплоход проходит за 4 часа такое же расстояние, какое проходит моторная лодка за 9 часов. Чему равна скорость моторной лодки, если скорость теплохода 36 км/ч? |
| 2 | На пропорциональное деление | таблица | Автотуристы в первый день были в пути 6 часов, а во второй - 4 часа. Всего они проехали 600 км. Какое расстояние проезжали туристы каждый день, если они ехали с одинаковой скоростью? | |
| 3 | Нахождение неизвестных по двум разностям | таблица | Два самолета летели с одинаковой скоростью. Один самолет был в воздухе 4 часа, а другой - 6 часов. Первый самолет пролетел на 1400 км меньше второго. Какое расстояние пролетел каждый самолет? |
2) по особенностям осуществляемого движения:
а) для одного объекта:
Таблица 19
| № | Виды задач | Форма краткой записи | Примеры задач |
| 1 | Движение в прямом и обратном направлении | таблица | Поезд проехал 400 км со скоростью 50 км/ч, а на обратном пути это расстояние он проехал в 2 раза быстрее. За сколько часов это расстояние проехал поезд на обратном пути? |
| 2 | Движение с остановками | таблица | Автомашина прошла сначала 160 км, потом половину этого расстояния. После этого оставалось пройти в 2 раза меньше того, что пройдено. За сколько часов машина прошла весь путь, если средняя скорость ее была 60 км/ч? |
| график движения | В выходной день отец и сын решили поехать в гости к друзьям в Тверь. Они сели в автобус, который выехал из Химок в 10 часов утра со скоростью 50 км/ч. Через 2 ч пути автобус сделал остановку на 30 мин, а затем продолжил путь со скоростью 60 км/ч. Через 1 ч после остановки автобус прибыл в Тверь, где отца и сына встречали их друзья. Каково расстояние от Химок до Твери? В котором часу автобус прибыл в Тверь? |
б) для двух объектов:
Таблица 20
| № | Виды задач | Основное понятие | Форма краткой записи | Обозначения на схеме |
| 1 | Встречное движение | Скорость сближения
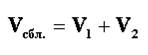
| Схема
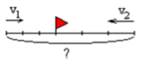
| Расстояние – отрезком.
Направление движения – стрелкой.
Место встречи или отправления– флажком.
Время движения (если дано) – соответствующим числом равных отрезков, длина каждого из которых равна v. |
| 2 | Движение в противоположных направлениях | Скорость удаления
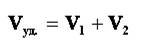
| Схема
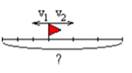
| |
| 3 | Движение вдогонку | Скорость сближения
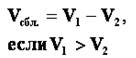
| Схема
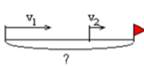
| |
| 4 | Движение с отставанием | Скорость удаления 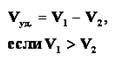
| Схема
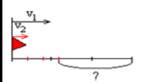
|
Таблица 21
| № | Виды задач | Примеры задач |
| 1 | Встречное движение | Из двух поселков выехали одновременно навстречу друг другу два велосипедиста и встретились через 2 часа. Один ехал со скоростью 15 км/ч, а второй со скоростью 18 км/ч . Найдите расстояние между поселками. |
| 2 | Движение в противоположных направлениях | Из города одновременно в противоположных направлениях выехали две машины. Скорость первой - 80км/ч. С какой скоростью ехала вторая машина, если через два час расстояние между ними было 340 км? |
| 3 | Движение вдогонку | Миша начал догонять Борю, когда расстояние между ними было 100м. Миша идет со скоростью 80м/мин, а Боря - со скоростью 60 м/мин. Через сколько времени мальчики встретятся? |
| 4 | Движение с отставанием | Собака гонится за лисицей со скоростью 750 м/мин, а лисица убегает от нее со скоростью 800 м/мин. Каким станет расстояние через 8 мин, если сейчас между собакой и лисицей 600 м? |
Задача: Из двух поселков выехали одновременно навстречу друг другу два велосипедиста и встретились через 2 часа. Один ехал со скоростью 15 км/ч, а второй со скоростью 18 км/ч . Найдите расстояние между поселками.
1 этап. Восприятие и осмысление задачи
Учитель совместно с учащимися составляет краткую запись в виде таблицы или схемы, отражающей особенности осуществляемого движения объектов.
.
| Скорость | Время | Расстояние |
| 15 км/ч | 2 ч |
? км ? км |
| 18 км/ч | 2 ч |
15 км/ч 18 км/ч
 |
? км
2 этап. Поиск плана решения
Схемы, используемые на этапе поиска плана решения задачи:
Таблица 22
Схемы, используемые на этапе поиска плана решения задачи
| Схема разбора от вопроса к данным | Схема разбора от данных к вопросу |
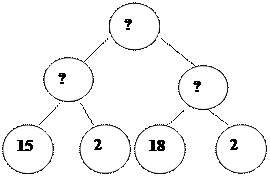 +
• •
+
• •
| 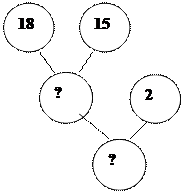 +
•
+
•
|
3 этап. Выполнение плана решения
Различные способы решения:
1 способ: 2 способ:
1) 15●2=30 (км) 1) 15+18=33 (км) - скорость сближения
2) 18 ● 2=36 (км) 2) 33●2=66 (км) - расстояние
3) 30+36=66 (км)
4 этап. Проверка решения
Решение задачи различными способами является способом проверки.
5 этап. Формулировка ответа на вопрос задачи (вывода о выполнении требования)
Ответ: 66 км расстояние между поселками.









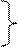 ? км
? км