Составные задачи в 2 и более действий, представляющие собой
различные сочетания простых
Задача: В коробке лежало 3 простых карандаша, а цветных на 2 карандаша больше. Сколько всего карандашей лежало в коробке?
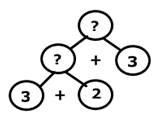
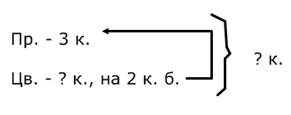
1) 3+2=5 (к.) - цветных карандашей
2) 5+3=8 (к.) - всего карандашей
Ответ: 8 карандашей лежало в коробке.
Задачи с величинами, связанными пропорциональной зависимостью
Это задачи, в которые входят тройки величин, связанных пропорциональной зависимостью (цена, количество, стоимость; скорость, время, расстояние и т.п.).
1) На нахождение четвертого пропорционального:
Рассматривая математическое содержание задачи на нахождение четвертого пропорционального, необходимо выяснить, какие значения из двух прямо пропорциональных величин даны, значение какой величины требуется найти.
Таблица 8
| ВЕЛИЧИНЫ | |||
| цена | количество | стоимость | |
| 1 | постоянная | даны два значения | дано одно значение, а другое является искомым |
| 2 | постоянная | дано одно значение, а другое является искомым | даны два значения |
| 3 | даны два значения | постоянное | дано одно значение, а другое является искомым |
| 4 | дано одно значение, а другое является искомым | постоянное | даны два значения |
| 5 | даны два значения | дано одно значение, а другое является искомым | постоянная |
| 6 | дано одно значение, а другое является искомым | даны два значения | постоянная |
Способы решения:
1) Способ приведения к единице: сначала узнают значение (цену) единицы одной из пропорциональных величин (товара, работы и пр.), затем значение (стоимость) указанного в условии количества. К единице приводят величину, для которой даны оба значения.
Например, задача: «На 6 одинаковых платьев израсходовали 30 м ткани. Сколько ткани потребуется на изготовление 3 таких платьев?» В задаче известны два значения количества и одно значение общего расхода. При решении способом прямого приведения к единице находим сначала расход на 1 платье: 30:6 =5(м). Затем определяем расход ткани на три одинаковых платья: 5•3=15(м).
2) Способ обратного приведения к единице сводится к нахождению соответствующего значения единицы той величины, для которой в условии указано лишь одно данное (одно значение).
Например, задача: «Для засолки 12 кг огурцов разложили в 6 одинаковых банок. Сколько потребуется таких банок, чтобы разложить 24 кг огурцов?» Учащиеся определяют, сколько раз по 12 кг содержится в 24 кг, т.е. во сколько раз 24 больше 12, значит, и банок получится во столько же раз больше: 6•(24:12)=12 (б.)
Задача: Мама купила несколько пирожков с капустой по 5 рублей за штуку и столько же пирожков с мясом по 10 рублей за штуку. За пирожки с капустой она уплатила 30 рублей. Сколько стоили пирожки с мясом?








