Факультет экономики и инвестиций
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ОБЛАСТНОЙ УНИВЕРСИТЕТ им. А.С. Пушкина
Факультет экономики и инвестиций
Кафедра экономики и управления
ЭКОНОМИКО – МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ:
МОДЕЛИ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Учебно-методическое пособие
для изучающих экономико-математическое моделирование
САНКТ – ПЕТЕРБУРГ - 2003
Автор:
К.э.н. Галанина Ольга Владимировна
Рецензенты:
К.э.н., профессор Рудакова Римма Прокопьевна
К.э.н. Попова Алла Леонидовна
Одобрена и рекомендована к печати методической комиссией факультета экономики и инвестиций, протокол №_____ от «_____»_______________2003г.
ОГЛАВЛЕНИЕ
| 1. Модели теории массового обслуживания. . . . . . . . . . . . . . . . . . . . . . . . | 3 |
| 2. Потоки событий. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 4 |
| 3. Анализ входного потока заявок. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 4 |
| 4. Анализ входного потока заявок на ЭВМ. . . . . . . . . . . . . . . . . . . . . . . . . | 6 |
| 5. Анализ потока обслуживания заявок. . . . . . . . . . . . . . . . . . . . . . . . . . . . | 7 |
| 6. Анализ потока обслуживания на ЭВМ. . . . . . . . . . . . . . . . . . . . . . . . . . | 8 |
| 7. Задачи для самостоятельного решения. . . . . . . . . . . . . . . . . . . . . . . . . . | 9 |
| 8. Графы состояний системы массового обслуживания. Система дифференциальных уравнений Колмогорова. . . . . . . . . . . . . . . . . . . . . | 10 |
| 9. Одноканальная СМО с отказами в обслуживании. . . . . . . . . . . . . . . . . | 11 |
| 10. Многоканальная СМО с отказами в обслуживании. . . . . . . . . . . . . . . . | 11 |
| 11. Одноканальная СМО с ограниченной очередью. . . . . . . . . . . . . . . . . . | 12 |
| 12. Одноканальная СМО с неограниченной очередью. . . . . . . . . . . . . . . . | 13 |
| 13. Многоканальная СМО с ограниченной очередью. . . . . . . . . . . . . . . . . | 14 |
| 14. Многоканальная СМО с неограниченной очередью. . . . . . . . . . . . . . . | 15 |
| 15. Задачи для самостоятельного исследования. . . . . . . . . . . . . . . . . . . . . . | 16 |
| 16. Реализация модели на языке VBA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 17 |
| Библиографический список использованной литературы. . . . . . . . . . . . . . | 19 |
| Приложение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 19 |
1. МОДЕЛИ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Теория массового обслуживания – раздел математики, изучающий различные состояния в системах массового обслуживания.
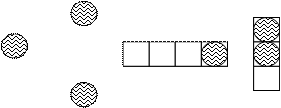 |
Система массового обслуживания (СМО) – совокупность каналов (пунктов) обслуживания, на которые в случайные моменты времени поступают заявки (требования), подлежащие удовлетворению.

заявки очередь каналы обслуживания
Рис.1. Графическая модель СМО
Заявки характеризуются:
l - интенсивность потока заявок (число заявок в единицу времени);
ротк – вероятность отказа в обслуживании (доля не обслуженных заявок).
Очередь характеризуется:
m – длина очереди; Lср – средняя длина очереди;
Точ – среднее время ожидания в очереди;
роч – вероятность попадания в очередь (доля заявок, попавших в очередь).
Каналы обслуживания характеризуются:
n – число каналов обслуживания;
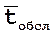 – среднее время обслуживания одной заявки;
– среднее время обслуживания одной заявки;
m - интенсивность обслуживания (число обслуженных заявок в единицу времени); 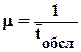 ;
;
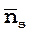 – среднее число занятых каналов;
– среднее число занятых каналов; 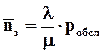 ;
;
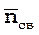 – среднее число свободных каналов;
– среднее число свободных каналов; 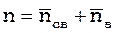 ;
;
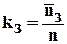 - коэффициент загрузки канала;
- коэффициент загрузки канала;
робсл – вероятность обслуживания (доля обслуженных заявок);
r - интенсивность нагрузки; 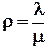 ;
;
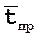 – среднее время простоя каналов.
– среднее время простоя каналов.
Другие характеристики СМО:
ТСМО – среднее время пребывания заявки в СМО;
LСМО – среднее число заявок в СМО.
2. ПОТОКИ СОБЫТИЙ

Поток событий – это последовательность появления событий, следующих одно за другим в случайные моменты времени.
Интенсивность потока событий –это число событий в единицу времени.
Поток событий называется стационарным, если его интенсивность – постоянная величина.

 |
Поток событий называется потоком без последствия, если количество событий за произвольно взятые не пересекающиеся промежутки времени взаимно независимы.
Поток событий называется ординарным, если события происходят по одному.
Поток событий называется простейшим, или пуассоновским, если он обладает свойствами стационарности, ординарности и без последствия.
У входящего пуассоновского потока заявок вероятность Р того, что число заявок, поступающих на обслуживание за промежуток времени k, рано l, определяется:
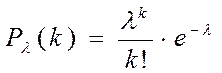 , где l - интенсивность потока заявок.
, где l - интенсивность потока заявок.
А поток обслуживания, в частности, случайная величина tобсл, подчиняется показательному закону распределения с плотностью вероятности:
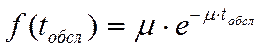 , где m - интенсивность обслуживания.
, где m - интенсивность обслуживания.
3. АНАЛИЗ ВХОДНОГО ПОТОКА ЗАЯВОК
Задача 1. Результаты наблюдения за потоком покупателей в секции универмага в течение 10 дней работы и проведения регистрации количества покупателей в течение каждого часа работы представлены в таблице 1.
Определить интенсивность входящего потока покупателей за час работы магазина и, используя критерий Пирсона (c2) с уровнем значимости a=0,05, обосновать предположение, что поток описывается пуассоновским законом распределения.
Таблица 1
| дни/часы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 2 | 4 | 2 | 3 | 4 | 3 | 5 | 2 |
| 2 | 3 | 2 | 3 | 2 | 7 | 2 | 3 | 3 |
| 3 | 1 | 3 | 4 | 3 | 4 | 6 | 4 | 2 |
| 4 | 4 | 4 | 4 | 5 | 9 | 3 | 4 | 4 |
| 5 | 2 | 1 | 3 | 7 | 3 | 6 | 2 | 3 |
| 6 | 3 | 2 | 3 | 4 | 5 | 5 | 3 | 2 |
| 7 | 4 | 3 | 4 | 3 | 8 | 3 | 4 | 3 |
| 8 | 1 | 2 | 2 | 4 | 3 | 4 | 2 | 4 |
| 9 | 3 | 4 | 6 | 3 | 4 | 2 | 4 | 2 |
| 10 | 2 | 2 | 3 | 5 | 6 | 4 | 2 | 5 |
Решение.
Сгруппируем данные по числу покупателей ki, посетивших магазин в течение часа (fi – эмпирические частоты, fiT – теоретические частоты). Заполняем таблицу 2. Теоретические частоты ищем по формуле:
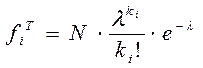 ,
, 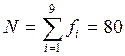 .
.
l - интенсивность потока:
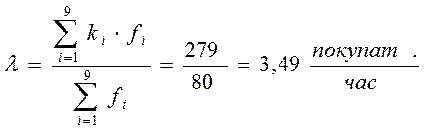 .
.
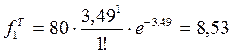 ,
, 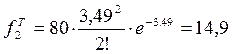 , ........
, ........
таким образом продолжаем заполнение таблицы 2.
Таблица 2
| ki | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| fi | 3 | 19 | 23 | 21 | 6 | 4 | 2 | 1 | 1 |
| fiT | 8,53 | 14,9 | 17,3 | 15,1 | 10,5 | 6,11 | 3,05 | 1,33 | 0,51 |
Вычисляем наблюдаемое значение Пирсона (c2наблюд):
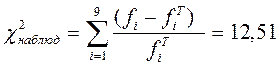 .
.
Для заданного уровня значимости a=0,05 и числу степеней свободы n=n-2=7, (где n – число групп в ряду) по таблице значений критических точек c2-распределения (см. приложение) находим c2критич(0,05; 7)=14,1.
c2наблюд<c2критич, т.к. 12,51<14,1, следовательно, гипотеза подтверждается, входящий поток покупателей описывается пуассоновским законом распределения с l=3,49.
4. АНАЛИЗ ВХОДНОГО ПОТОКА ЗАЯВОК НА ЭВМ
Решим задачу 1 с использованием программы MS Excel.
1. Открываем новый документ MS Excel.
В ячейки А2:А10 вводим значения ki;
в ячейки В2:В10 вводим эмпирические частоты fi;
в ячейку В11 записываем формулу для подсчета суммарного числа N:
=СУММ(В2:В10)
2. Для нахождения значения l :
в ячейку С2 запишем формулу =В2*А2, копируем эту формулу в диапазон С3:С10, получили значения fi*ki;
в ячейку С11 запишем формулу =СУММ(С2:С10)/$ B $11- это формула для нахождения l.
3. В ячейку D 2 записываем формулу для нахождения теоретических частот fT: =($ B $11*$ C $11^ A 2* EXP (-$ C $11))/ФАКТР(А2);
копируем эту формулу в диапазон D 3: D 10.
4. Для нахождения наблюдаемого значения c2наблюд :
в ячейку Е2 записываем формулу =( B 2- D 2)^2/ D 2,
копируем эту формулу в диапазон Е3:Е10;
в ячейке Е11 запишем формулу =СУММ(Е2:Е10) – получили значение c2наблюд.
5. Для уровня значимости a=0,05 и числу степеней свободы n=n-2=7 найдем в ячейке E 13 критическое значение c2критич: =ХИ2ОБР(0,05;7).
6. Визуально сравниваем значения ячеек E 11 и E 13. Если значение E 11<E 13, значит, гипотеза подтверждается. В противном случае, гипотеза не подтверждается (см. рис.2).
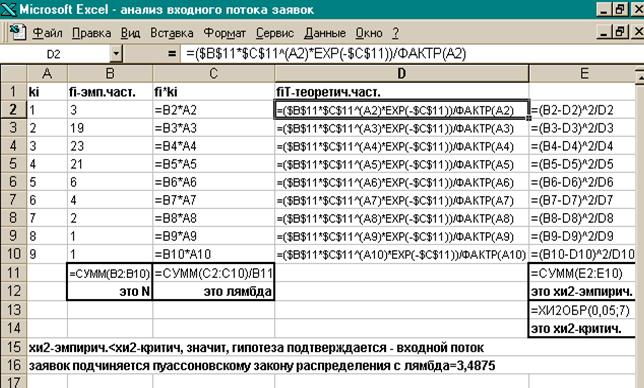
Рис.2. Так должны быть записаны формулы для задачи 1
5. АНАЛИЗ ПОТОКА ОБСЛУЖИВАНИЯ ЗАЯВОК
Задача 2. Результаты регистрации продолжительности обслуживания покупателей в обувной секции универмага представлены в таблице 3.
Таблица 3
| номер интервала | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Интервал времени обслуживания | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 | 30-35 | 35-40 |
| Частота f | 17 | 20 | 19 | 11 | 9 | 6 | 3 | 1 |
Определить среднее время обслуживания tобсл и интенсивность обслуживания m. По критерию Пирсона (c2) с уровнем значимости a=0,05 обосновать предположение, что время обслуживания распределяется по показательному закону.
Решение.
1. Для каждого интервала Dti вычисляем его середину по формуле:
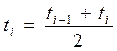 , i=1...8. Результаты запишем в таблицу 4.
, i=1...8. Результаты запишем в таблицу 4.
Таблица 4
| N интервала | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ti | 2,5 | 7,5 | 12,5 | 17,5 | 22,5 | 27,5 | 32,5 | 37,5 |
| fi | 17 | 20 | 19 | 11 | 9 | 6 | 3 | 1 |
| fiT | 27 | 19 | 13 | 9 | 6 | 4 | 3 | 2 |
2. Вычислим среднее время обслуживания tобсл и интенсивность обслуживания m по формуле:
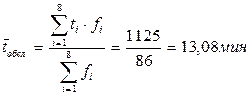 ,
, 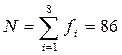 .
.
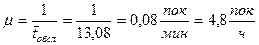 .
.
3. Найдем теоретические частоты fiT по формуле:
fiT=Dt×m×N×e-m×ti,
f1T=5×0,08×86×e-0,08×2,5=32,87×e-0,2=26,91;
f2T=5×0,08×86×e-0,08×7,5=34,4×e-0,6=18,87;......
Запишем результаты в таблицу 4.
4. Вычислим наблюдаемое значение Пирсона (c2наблюд):
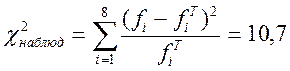 .
.
5. По заданному уровню значимости a=0,05 и числу степеней свободы n=n-2=8-2=6, где n – число групп в ряду. По таблице значений критических точек c2-распределения найдем его критическое значение c2критич(0,05;6)=12,59.
6. Сравниваем c2наблюд и c2критич: 10,7<12,59, следовательно, гипотеза подтвердилась, время обслуживания покупателей подчиняется показательному закону с интенсивностью m=4,8 покупателя в час.
6. АНАЛИЗ ПОТОКА ОБСЛУЖИВАНИЯ НА ЭВМ
Решим задачу 2 с использованием программы MS Excel.
1. Открываем новый лист MS Excel.
В диапазон ячеек А2:А9 записываем значения ti;
в диапазон ячеек В2:В9 вводим эмпирические частоты fi;
в ячейку А10 записываем формулу для нахождения Dt: =А3-А2;
в ячейку В10 записываем формулу для N: =СУММ(В2:В9);
2. в ячейку С2 записываем формулу для нахождения fi×ti: =А2*В2; копируем эту формулу в диапазон С3:С9;
в ячейку С10 записываем формулу для tобсл: =СУММ(С2:С9)/$ B $10;
в ячейку С12 запишем формулу для m (в мин-1): =1/С10
3. Заполним столбец теоретических частот fTi, для этого в ячейку D2 запишем формулу: =$ A$10*$ C$12*$ B$10* EXP(-$ C$12* A2), копируем эту формулу в диапазон ячеек D3: D9.
4. В ячейку Е2 записываем формулу =( D2- B2)^2/ B2, копируем эту формулу в диапазон E3: E9;
в ячейке Е10 суммированием находим наблюдаемое значение c2наблюд: =СУММ(Е2:Е9).
5. В ячейке Е12 для уровня значимости a=0,05 и числа степеней свободы n=6 находим критическое значение c2критич: =ХИ2ОБР(0,05;6).
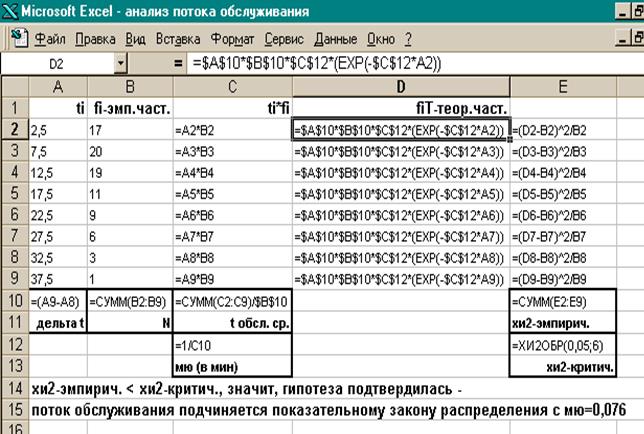
6. Сравниваем значения ячеек Е10 и Е12. Если значение Е10<Е12, то гипотеза подтверждается (см. рис.3).
Рис.3. Так должны быть записаны формулы для задачи 2
7. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ








