ПЕРЕЧЕНЬ ТЕМ ДЛЯ ПОДГОТОВКИ К ТЕОРЕТИЧЕСКОЙ ЧАСТИ ЭКЗАМЕНА ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА. ЧАСТЬ 3 (Обыкновенные дифференциальные уравнения и ряды)
1. Обыкновенные дифференциальные уравнения (ДУ). Основные понятия: порядок уравнения, частное решение, общее решение, общий интеграл, интегральная кривая, решение задачи Коши. Существование и единственность частного решения ДУ I-го порядка
2. Типы ДУ I-го порядка и методы их решения. ДУ с разделяющимися переменными; однородные ДУ I-го порядка; линейные ДУ I-го порядка, уравнение Бернулли; ДУ в полных дифференциалах, интегрирующий множитель вида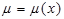 
и 
.
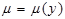3. ДУ II-го порядка, допускающие понижение порядка.
4. Линейные ДУ II-го порядка Свойства их решений.
5. Линейная зависимость и независимость функций. Определитель Вронского. Фундаментальная система решений. ЛОДУ II-го порядка.
6. Структура общего решения ЛОДУ II-го порядка. Построение общего решения ЛОДУ II-го порядка с постоянными коэффициентами методом Эйлера.
7. Структура общего решения ЛНДУ II-го порядка. Подбор частного решения ЛНДУ II-го порядка в случае правой части специального вида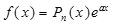 
и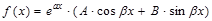 
. Метод неопределенных коэффициентов.
8. Метод вариации произвольных постоянных для решения ЛНДУ II-го порядка.
9. ЛДУ n-го порядка: основные понятия, свойства решений, структура общего решения. Построение общего решения ЛОДУ n-го порядка с постоянными коэффициентами методом Эйлера.
10. Системы ДУ I-порядка. Метод исключения неизвестных(или метод сведения к одному дифференциальному уравнению более высокого порядка) в решении систем ДУ I-порядка.
Ряды
1. Числовые ряды. Основные понятия: сумма и сходимость ряда. Свойства сходящихся рядов.
2. Необходимый признак сходимости ряда. Признаки сходимости рядов с положительными членами: интегральный признак Коши, признаки сравнения, признак Даламбера и радикальный признак Коши.
3. Ряды Дирихле, условия их сходимости. Гармонический ряд.
4. Знакопеременные ряды: понятия абсолютной и условной сходимости. Признак абсолютной сходимости знакопеременного ряда, признак Лейбница. Свойства абсолютно и условно сходящихся рядов.
5. Степенные ряды. Радиус, интервал, область сходимости степенного ряда. Теорема Абеля. Свойства степенных рядов.
6. Разложение функций в ряды Тейлора и Маклорена. Применение степенных рядов для приближенных вычислений и решения ДУ.