Тема. Метод внутренней нормы прибыльности.
Использование метода полинома рассмотрим на примере проекта, который характеризуется следующим численным рядом:
-100 10 10 100 д. ед.

0 1 2 3 годы
Рис. 4 Исходные данные для расчета эффективности методом полинома
Для определения внутренней нормы прибыли составим уравнения чистой дисконтированной стоимости:
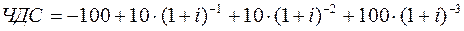
В случае, когда i = r уравнение имеет вид:
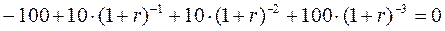
Для упрощения принимаем, что 1+r=х. Уравнение принимает следующий вид:
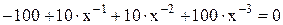
Умножим уравнение на х3:
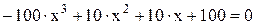
Это уравнение представляет собой полином третьей степени. Его можно решить методом касательных, согласно которому значение неизвестного параметра устанавливается путем поэтапного подбора. На первом этапе оно задается произвольно. На следующих этапах уточнение осуществляется по формуле:
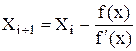 . .
| (8) |
Количество этапов определяется обеспечением требования хi+1 = хi .
В качестве отправной точки примем х = 1,1. Значения составляющих формулы соответственно характеристик данного проекта определяется следующим образом:
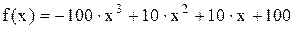
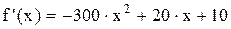
Первая итерация:
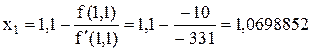
Вторая итерация:
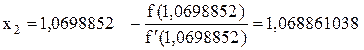
Третья итерация:
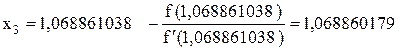 .
.
В связи с тем, что полученные в результате третьей итерации значение х2 почти не отличается от значения х3, принимаем как итоговый результат х = 1,068860179. Таким образом, внутренняя норма прибыли составляет 6,89%. Для оценки достоверности полученного результата используем критерий дисконтированной стоимости, соответственно которого при значении процентной ставки на уровне внутренней ренты этот показатель равен нулю.
і = r
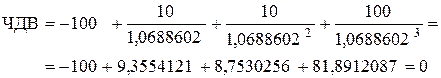
Как видно из расчетов при i = r дисконтированная стоимость капитала равна нулю, что подтверждает правильность полученного значения внутренней нормы прибыли.
Другим методом определения уровня внутренней нормы прибыли является метод хорды. На рис. 22 приведена зависимость чистой дисконтированной стоимости от процентной ставки. Задача касается определения координат точки пересечения кривой К1К2 с горизонтальной координатной осью. В случае, когда эта линия будет минимально короткой, эти координаты практически совпадают с координатами точки М, находящейся в месте пересечения с горизонтальной координатной осью прямой линии К1К2, которая представляет собой хорду.
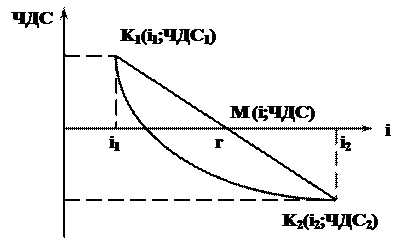
Рис. 22. Зависимость ЧДС от процентной ставки дисконтирования
Известным в математике является уравнение хорды, которое в общем виде отражает взаимосвязь координат трех точек:
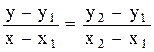 . .
| (9) |
С учетом сущности анализируемых показателей, это уравнение можно представить в следующем виде:
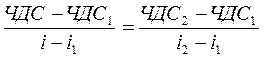 . .
| (10) |
Подставил известны координаты точки М (ЧДС = 0; i = r), получим следующее:
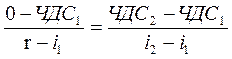 . .
| (11) |
Преобразуем уравнение путем возведения его в минус первую степень:
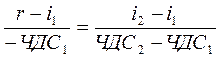 | ∙ (-ЧДC1); | ∙ (-ЧДC1);
| (12) | |
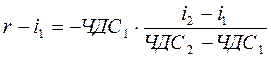 . .
| (13) |
В результате получаем формулу расчета внутренней нормы прибыли:
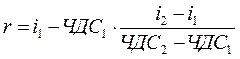 . .
| (14) |
Расчет внутренней нормы прибыли методом хорды осуществляется по следующим этапам:
1. Составить уравнения расчета чистой дисконтированной стоимости инвестиции, которая подвергается анализу.
2. Произвольно задать два значения процентной ставки i1 и i2, предполагая, что значение внутренней нормы прибыли находится в интервале между ними.
3. Рассчитать значение чистой дисконтированной стоимости для заданных значений i1 и i2. Если ЧДC1> 0, а ЧДС2 <0, то переходим к следующему этапу. Если это требование не выполняется, то необходимо скорректировать i1 или i2 и повторно выполнить расчеты.
4. Определить величину внутренней нормы прибыли используя формулу 36.
5. Сделать вывод об эффективности каждого варианта инвестирования в соответствии с критерием.
6. Выбрать наиболее выгодный вариант инвестирования, исходя из требования максимизации значение внутренней ренты.
Рассмотрим использование метода хорды для расчета внутренней нормы прибыли в условиях предыдущего примера: -100, 10, 10, 100.
Зададим два значения процентной ставки: і1 = 5 %; і2 = 10 %. Рассчитаем соответствующие значения чистой дисконтированной стоимости:
і1 = 5 %
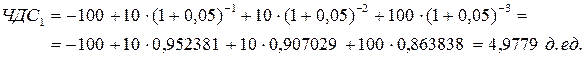
i2 = 10%
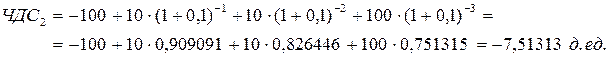
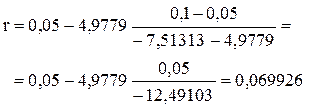
r = 6,99 %
Отклонение полученного знания от предыдущего метода определения внутренней ренты обусловлено погрешностями расчета. Следует указать, что чем короче будет хорда, тем выше точность показателя.








