Практикум по профессии “Оператор ЭВМ и ВМ” – день 3й
Тема 4. Система MS Word – набор текста, таблиц, формул по образцу
Задание №1. Создать файл MS Word, набрать и отредактировать тексты по предоставленному образцу.
Задание №2. Созданный файл прикрепить в ленте учебного паблика в комментариях указанной записи УП день 3, сохранить файл для распечатки в приложении отчета
Вариант 3
1.4.1 Головоломки
Головоломка – это сложная, трудноразрешимая загадка, задача.
Приведем следующую классификацию головоломок:
1. Языковые (загадки, анаграммы, криптограммы, ребусы,
кроссворды);
2.Графические(оптические иллюзии, геометрические, лабиринты);
3. Логические (на дедукцию, противоречия, парадоксы);
4. Математические (магические квадраты, алгебраические, задачки,
крипто загадки);
5. Игры с элементами головоломок (игры на перестановки механические и
сборные игры, игры с картами и костями).
Использование головоломок – эффективный инструмент повышения
интереса студентов к предмету.
Применение головоломок на уроках информатики дает возможность, и
повысить мотивацию студентов, и дать им знания.
Особенности и некоторые преимущества названных выше типов
занимательных задач проведены таблице.
Таблица 1. Классификация занимательных задач
| Тип задач | Особенности | Расширение Возможностей обучающего | Результат для обучаемого |
| Задачи-рисунки | Несоблюдение истинных размеров предметов с размерами изображения. Например, на рисунке дискета может быть такого же размера, что и сканер | Формирование умений видеть предметы в необычных ракурсах, развитие творческих, способностей, наглядно-образного мышления, Пространственного и плоскостного восприятия предметов организация совместной коллективной деятельности | Умения глубже проникать в суть явлений, правильно ставить вопросы и анализировать ответы развитие интуиции, исследовательских навыков, зрительного внимания, абстрактного мышления |
Алфавитный указатель
Адлеман, Лен 104
Алгоритм
- Аль-Кинди 7, 38-39,40
- Диффи – Хеллмана 100-103
- Луна 89-90
- перестановочного шифрования
22-25, 57-59
- подстановки 24-25, 48, 49, 57 –
59, 62б 99
- шифрования 11-11, 18, 19, 22,
35,
-DES (“стандарт шифрования данных”)
99, 113, 118
- RSA 104-107, 109, 113, 118, 121,
133, 134, 136, 137
-TLS (“безопасность транспортного
уровня”) 112
Алфавит
- открытого сообщения 31, 36, 43,
44,45
-шифроалфавит 26, 27, 36-37
42-45,49-51,127
Альберти
- диск 45, 60
- Леон Баттиста Альберти 42-43
Байт 77-81
Безу, соотношение 134
Бит 77, 83 ,116, 117, 122
-квантовый 116-118
-контрольный (бит чесности)
84-85
Блетчли-Парк 69-72
Бэббидж, Чарльз 46, 49-51
“Бэкдоры” (“черные ходы”) 103
Виженер
-Блез де Виженер 43
- квадрат Виженера 43 47,49,50,128
Гейзенберг, Вернер 113,118-119
Двоичная система счисления 8,9,10,77-79,80,81-
83,84,88,92,95
Десятичная система счисления 10, 79, 82-83
Диффи, Уитфилд 100-104-109
Евклид 27, 33
Избыточность информации 84
Касиски, Фридрих 51
Ключ 10-14
-асимметричный 102,133
-закрытый 13-14, 103, 105-106,
109,110,112
-открытый 13-14, 103,105-106,108,109-112,133
-распределение 99,121
-шифроблокнот одноразового назначения 121-124
Ключевое слово 36-37, 46-47, 49-51, 58-60,129
Коды
-Морзе 53-56, 60
-траншейные 62
-штрихкод 92-97
-ASCII 77-78,81-83,87,105
2.Вставьте картинку по временам года (рис. 3.2).
Рис. 3.2
ПРИЛОЖЕНИЕ
Работая по модулю, возьмем НОД (a, n) = 1, тогда обязательно существуют целые числа p и q , такие что pa + qn = 1. Так как n – модуль, то qn = 0, следовательно, существует такое p, что pa = 1, то есть существует число, обратное числу a по модулю n, а именно p.
Элементы, имеющие обратный элемент по модулю n, являются натуральными числами, которые меньше, чем n, и удовлетворяют условию НОД (a, n) =1. Количество таких чисел называется функцией Эйлера и обозначается как ф(n).
Если число n представлено в виде произведения степеней простых чисел следующим образом n =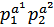 
… 
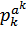, то
ф(n)=n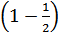 
… 
.
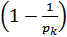Например, если n = 1600 =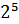 
* 
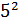, то
ф(1600) = 160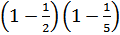0 
=640
Более того, в случае, если n – простое число, то для любого значения a выполняется НОД (a, n) = 1, и, следовательно, любое число a будет иметь обратное по модулю n, значит ф(n) = n – 1
Итак, подведем итог самым важным фактам.
1. ф(n) называется функцией Эйлера и обозначает количество натуральных числе, меньших n и взаимно простых с ним
2. Если n = pq, где p и q простые числа, то
ф(n) = (p – 1) (q – 1)
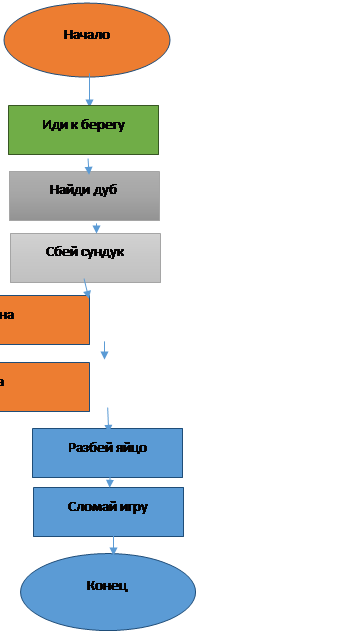
3. Из малой теоремы Ферма мы знаем, что если a – целое число, большее нуля, и p – простое число, то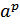 
= a (mod p), что эквивалентно 
= 1 (mod p)
В заключении мы используем функцию Эйлера, подставив ее в предыдущее соотношение.
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||