Как мы можем измерить длину береговой линии?
Английский ученый Льюис Ричардсон (Lewis F. Richardson) первым занялся проблемой расчета длины береговой линии, или любой другой государственной границы. Эта проблема была позднее решена Мандельбротом. На первый взгляд это кажется глупой задачей, но фактически она поднимает очень серьезные вопросы, касающиеся жизнеспособности евклидовых измерений для определенных классов объектов и для рынков.
Представьте себе, что вы получили задание измерить береговую линию Флориды. Ваш босс хочет получить точные измерения и дает вам 10-футовый шест. Вы обходите весь периметр полуострова. Вы заканчиваете работу и вычисляете ответ. Затем ваш босс решает, что 10-футовый шест приводит к потере слишком многих деталей, дает вам ярд, и вы получаете приказ повторить процедуру. Вы заново проделываете всю работу и получаете значительно большую величину. Использование однофутовой линейки даст еще большую величину береговой линии, а если вы будете использовать однодюймовую линейку и не сойдете с ума, то ответ ваш вырастет чуть ли не до бесконечности. Чем короче инструмент измерения, тем больше деталей вы захватываете. Береговая линия представляет собой класс объектов, которые имеют бесконечную длину в конечном пространстве.
Длина береговой линии не является величиной, которую можно измерить с помощью евклидового подхода к измерениям. Если бы Флорида имела гладкую евклидову форму, то на вопрос о ее длине существовал бы конечный ответ. Но практически все существующие в природе формы являются неправильными. Они отрицают абсолютные величины традиционных измерений.
Мандельброт изобрел новый способ измерения таких неправильных естественных объектов, или естественных систем. Он назвал его фракталом или, более правильно, фрактальным измерением. Фрактальное измерение является степенью грубости, или неправильности, структуры или системы. Мандельброт нашел, что фрактальное измерение остается постоянным в течение нескольких степеней увеличения неправильного объекта. Иными словами, в любой неправильности существует правильность. Когда мы обычно называем явление случайным, мы указываем тем самым, что не понимаем структуру этой случайности. Относительно рынка это означает, что в различных временных структурах должны существовать фигуры одной и той же формы. Минутный график будет содержать те же фрактальные фигуры, что и месячный график. Это сходство, найденное на графиках и фьючерсов, и акций, дает дальнейшее указание на то, что поведение рынка более сходно с парадигмой естественного поведения, чем с экономическим, фундаментальным, механическим или техническим поведением.
Мандельброт также нашел близкое сходство между фрактальным числом реки Миссисипи и ценами на хлопок в течение всех тех временных периодов, которые он изучал, и которые включали мировые войны, наводнения, засухи и тому подобные катастрофы. Нельзя преувеличить значение этого наблюдения. Оно означает, что рынки являются естественной нелинейной функцией, а не функцией классической линейной физики. И это объясняет, по крайней мере, частично, почему постоянно проигрывают 90 процентов трейдеров, использующих технический анализ. Технический анализ не только основывается на ложной предпосылке, что будущее повторяет прошлое, но и использует для анализа неуместные линейные технические приемы.
Также как евклидовский анализ не может точно измерить длину береговой линии Флориды, не может он и точно измерить поведение рынка. Электрическая деятельность сердца является фрактальным процессом, такой же является и деятельность иммунной системы. Бронхи, легкие, печень, почки и система кровообращения - все это фрактальные структуры. Вся физическая структура человека, похоже, является по природе своей фрактальной; и, пожалуй, самое важное, структура человеческого мозга также фрактальна. Предполагается, что для того, чтобы работать вообще, человеческая память, мыслительный процесс и самосознание должны быть по структуре и функционированию фрактальными.
С учетом вышесказанного будет разумным предположить, что любая закономерность, являющаяся результатом человеческого взаимодействия (например, рынки), должна также иметь фрактальную структуру. Это означает, что рынок создается турбулентной коллективной деятельностью и является нелинейным явлением.
Любой трейдер, обладающий хоть небольшим опытом, знает, что рынки не являются простым механическим результатом спроса и предложения. Если бы люди были машинами, поведение акций было бы простой двухмерной системой сил предложения и спроса. Маятник, подвешенный между двумя магнитами, является простой двухмерной системой притяжения (см. Рисунок 2.2). Двухмерные системы притяжения просты, линейны и скучны. Двухмерный рынок не имел бы ни сложности, ни нелинейности, ни турбулентности, ни волатильности.
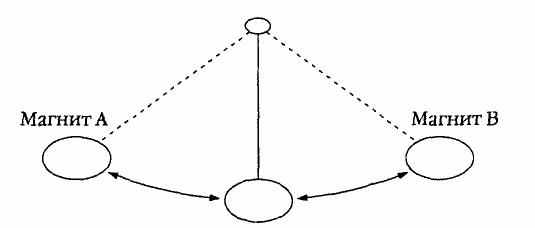
Рисунок 2.2
Если вблизи маятника поместить третий полюс притяжения, то в систему будет введен хаос, или фрактальная структура. В нашем моделировании мы размещаем пять различных центров притяжения, которые влияют на движение цены от одного края до другого. Система эта является нелинейной, динамичной и хаотичной. И она работает.
Поскольку рынки являются нелинейной турбулентной системой, созданной взаимодействием человеческих существ, поведение цены и времени являются идеальными местами для поиска фрактальных структур. Вновь и вновь турбулентные процессы в природе создают удивительные по сложности структуры, не имеющие беспорядочности, в которых можно наблюдать взаимное сходство. Нахождение фрактальной структуры рынка дает способ понимания поведения всей системы - а именно, движения цены определенного фьючерса или акции. Так можно увидеть закономерность, порядок и, что самое важное, предсказуемость там, где другие видят только хаос.
Главной целью данной книги является показать вам, как торговать, используя фрактальную геометрию. Двадцать три года интенсивных исследований были посвящены фрактальной геометрии рынков. Чтобы не утомлять вас подробностями этих исследований, приведем здесь лишь один пример того, как фрактальный анализ вносит вклад в лучшее понимание торговых инструментов для рынков.
Фракталы получаются на компьютерных экранах путем использования процесса, получившего название итерация. Аккреция (наращивание) представляет собой несистематическую итерацию. Что-то прибавляется к чему-то, затем эта большая величина прибавляется к чему-то еще и т.д. Простейшею моделью итерации является сложение последовательности, известной как числа Фибоначчи. Эта последовательность начинается с О, и первыми двумя величинами являются 1 и 1. Добавьте 1 к первому числу О, и ответ будет 1. Добавьте вторую 1, и ответ будет 2. После этого складываются вместе два рядом стоящие числа, и получается следующее число данного ряда. Таким образом, складываются 1 и 2, и ответ получается 3. Складываются 2 и 3, и ответ получается 5. Сложите 3 и 5 и получите ответ 8. Сложите 5 и 8, и ответ будет 13. Последовательность продолжается до бесконечности. Любопытным свойством этого процесса итерации является то, что каждое число последовательности составляет точно 0,618 следующего числа вне зависимости от того, какие числа последовательности рассматриваются. Отношение 0,618 является неизменным продуктом систематической аккреции. (Аккре́ция (лат. accrētiō «приращение, увеличение» от accrēscere «прирастать»)
Мир полон связями 0,618. Расположение семян в цветах представляет собой числа Фибоначчи. Сердечная мышца сокращается в течение 0,618 продолжительности времени, которое отдыхает. Идеальная структура 0,618 демонстрируется раковиной наутилуса. Более личным примером является пупок человека, расположенный на 0,618 высоты человека. Были исписаны целые тома, где просто перечисляются и классифицируются случаи проявления в природе этого феномена числа 0,618.
Розеттским камнем фрактальной геометрии является набор Мандельброта, показанный на Рисунке 2.3. Набор Мандельброта, главный фрактал и строительный элемент фрактальной геометрии, создается построением на графике чисел, получающихся из итерации полинома второй степени на сложной плоскости.
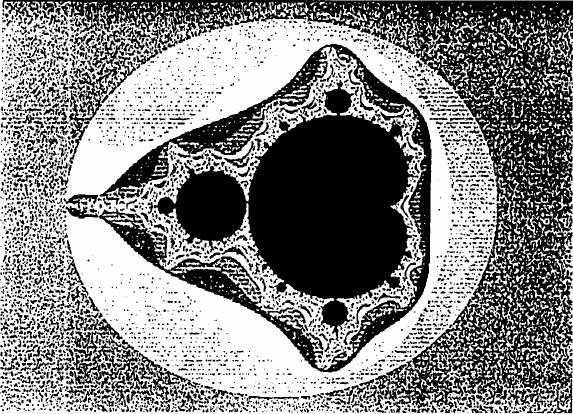
Рисунок 2.3
Набор Мандельброта структурирован в отношениях Фибоначчи 0,618. Он почти исключительно состоит из спиралей. Если вы поставите раковину наутилуса на вершину, и будете вращать ее, то получите фигуру, очень напоминающую набор Мандельброта. Этот набор может весьма вероятно быть ключевым камнем, который связывает числа Фибоначчи, волны Эллиотта (см. Главу 7 в книге "Торговый хаос", где подробно полностью описываются волны Эллиотта) и фракталы в одно неразделимую парадигму.
В своих собственных исследованиях Profitunity Trading Group открыла несколько повторяющихся закономерностей, которые позволяют до определенной степени предсказывать будущие движения рынка, что является гигантским прыжком вперед по сравнению с общепринятым техническим анализом. Эти вопросы описываются в Главах 8-12.








