Энтропия и вероятность

Дата: 2025-04-30; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Физический смысл энтропии можно установить из тесной связи с термодинамической вероятностью системы. Выше мы показали, что при самопроизвольных процессах в системе энтропия возрастает, приводя систему в более вероятностное состояние, которое является равновесным. Т.е. возрастание энтропии приводит к росту термодинамической вероятности системы. Больцман установил:

 

S = k ln W, (6)

 

где k– постоянная Больцмана, W– термодинамическая вероятность.

Уравнение Больцмана – энтропия системы пропорциональна логарифму термодинамической вероятности.

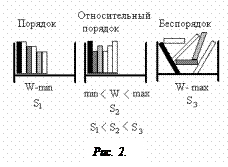Термодинамической вероятно­стью называется число микро­состояний, соответствующих данному макростоянию сис­темы. В качестве примера рассмотрим книжную полку с книгами (рис.2).

Если книги расположить строго по высоте, то возможность переставить их на полке имеет минимальное число. Т.е. число перестановок книг на полке (число микросостояний), удовлетворяющих условию макросостояния (книги располагаются по высоте), минимально, а порядок максимален. И, наоборот, если книги лежат как угодно, то выполнить это условие возможно бесконечным числом перестановок. Т.е. беспорядок имеет максимальное число микросостояний, и он легко наступает. Этот рисунок показывает, что в природе естественным образом все стремится к беспорядку (он легче наступает), т.е. к максимальному значению энтропии.

Свободная и связанная энергия

Выясним еще один физический смысл энтропии, как меру «обесцененности» энергии. Рассмотрим обратимое расширение газа при постоянной температуре (с теплообменом).

Согласно первому началу термодинамики: dQ = dU + dA

Второе начало можно представить dS = dQ / T Þ dQ = TdS

Объединяя выражения, получим TdS = dU + dA

Так как Т – постоянна, то dA = – d ( U – TS ).

Полученное выражение показывает, что в работу переходит лишь (U – TS) часть внутренней энергии, которая называется свободной энергией и обозначается


F = U – TS .

Внутренняя энергия TS не может перейти в работу. Эта часть энергии называется связанной энергией. Она как бы обесценивается с точки зрения возможности превращения этой части внутренней энергии в механическую работу. Чем больше энтропия, тем больше «обесцененная» часть энергии. В этом смысле энтропию называют мерой «обесценивания» энергии.

 

Теория метода

В данной работе рассматривается изменение энтропии при плавлении олова. Процесс плавления олова можно рассматривать в два этапа: I –нагревание от комнатной температуры Тк до температуры плавления Тп, II – плавление.

Изменение энтропии на первом этапе можно определить:

 

.

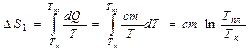Изменение энтропии на втором этапе:

 

.

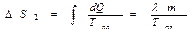Полное изменение энтропии равно:

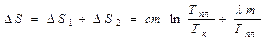. (7)

 

Для определения изменения энтропии необходимо определить температуру плавления олова. Эту температуру определяют из условия, что при плавлении температура не изменяется. Постоянная температура при плавлении обусловлена тем, что теплота, поступающая от нагревателя, расходуется не на повышение температуры олова (т.е. не на увеличение кинетической энергии атомов в кристаллической решетке), а на разрушение кристаллической решетки. И пока существует хотя бы одна атомарная связь, температура олова не повысится. Поэтому, если снимать зависимость температуры нагрева олова от времени, то обнаружим, что некоторое время температура не изменяется. Это и есть температура плавления олова.

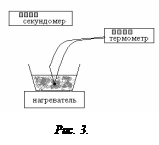
Описание эксперимента

 

Включите нагреватель и термометр (рис.3). Нагрев вести до температуры, заданной преподавателем включите секундомер и начните заполнять табл. 1.

 

Таблица 1

Время (с)        
Температура олова (К)        

 

Определив из таблицы температуру плавления и воспользовавшись формулой (7), рассчитайте изменение энтропии. Полученные результаты занесите в табл. 2.

 

Таблица 2

m (кг) c (Дж/кгК) l (Дж/кг) Тпл (К) Тк (К) DS (Дж/К)
           

 

Расчет погрешности

 

Относительная ошибка: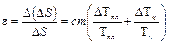

Абсолютная ошибка: Δ(Δ S ) = Δ S ε

Задачи

1. Найти изменение энтропии 1 кг воды при нагревании ее в чайнике от 200 до кипения (1000С).

Ответы: 1) 500 Дж/К; 2) 25,5 Дж/К; 3) 125 Дж/К; 4) 103 Дж/К; 5) 230 Дж/К.

2. Идеальная тепловая машина получает от нагревателя температура которого 500 К за один цикл 3360 Дж теплоты. Найти количество теплоты, отдаваемое за один цикл холодильнику, температура которого 400 К.

Ответы:1) 2688 Дж; 2) 3273 Дж; 3) 685 Дж; 4) 931 Дж; 5) 5850 Дж.

3. Температура холодильника идеального теплового двигателя равна 270С, а температура нагревателя на 900С больше. Каков КПД этого двигателя?

Ответы:1) 30 %; 2) 23 %; 3) 46 %; 4) 77 %; 5) 66 %.

4. Определить изменение энтропии 10 г воды при отвердении ее в лед при 00С.

Ответы:1) –20,8 Дж/К; 2) 17,7 Дж/К; 3) –56,4 Дж/К; 4) –12,3 Дж/К; 5) 31,7 Дж/К.

5. Газ совершающий цикл Карно за счет каждых 2 кДж энергии, полученной от нагревателя, производит работу 600 Дж. Во сколько раз абсолютная температура нагревателя больше абсолютной температуры холодильника?

Ответы:1) 1,3; 2) 1,4; 3) 1,6; 4) 1,5; 5) 1,7.

6. Определить изменение энтропии 20 г олова при изменении температуры от 270С до 2100С. (с=0,23.103 Дж/кг.К)

Ответы: 1) 12,8 Дж/К; 2) 2,35 Дж/К; 3) 4,39 Дж/К; 4) 17,8 Дж/К; 5) 2,16 Дж/К.

 

Контрольные вопросы

1. Второе начало термодинамики.

2. Чему равно КПД тепловой машины, цикла Карно?

3. КПД каких тепловых машин максимально?

4. Свойства энтропии.

5. Формула Больцмана для энтропии. Физический смысл энтропии.

6. Свободная и связанная энергия.

7. Вывод рабочей формулы.

8. Почему процесс плавления идет при постоянной температуре?

9. Объясните график плавления кристаллических тел.

 

Литература

1. Савельев И. В. Курс общей физики, т. 1. М.: Наука, 1989. с. 289–300.

2. Трофимов a Т. И. Курс физики. М.: Высшая школа, 2002, с.111–114.

3. Детлаф А. А., Яворский Б. М. Курс физики, М.: Высшая школа, 1989, с.129, 133.

Лабораторная работа 1.14