Изохорический процесс
При изохорическом процессе V=const, dV=0 и dA=0. Т.е. при этом процессе работа не совершается, т.к. объем не изменяется. Тогда 1 начало запишется:
dQ = dU .
Т.е. количество теплоты расходуется на изменение внутренней энергии. Но по определению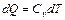 
(для 1 моля). Следовательно, 
.
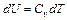Из этой формулы видно, что изменение внутренней энергии газа определяется только изменением его температуры. Теплоемкость при постоянном объеме (изохорная теплоемкость) равна:
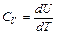(12)
Изобарический процесс
В этом процессе изменяются и внутренняя энергия, и работа против внешних сил:
dQ = dU + dA ,
т.е. теплота, подводимая к системе, идет на увеличение внутренней энергии и на совершение работы против внешних сил.
Для 1 моля газа уравнение Менделеева–Клапейрона
pV = RT ; pdV = RdT,
но pdV = dA, поэтому dA = RdT, тогда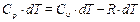 
(Напомним, что С u и Cp – мольные теплоемкости)
Cp = Cv + R, (13)
R – универсальная газовая постоянная, равная работе расширения одного моля газа при нагревании на один градус в изобарическом процессе.
Уравнение (13) называется уравнением Роберта Майера. Из него следует: при изобарном нагревании 1 моля газа на 10 часть теплоты, равная CV, идет на увеличение внутренней энергии, а другая часть, равная R , – на совершение работы против внешних сил.
Адиабатический процесс
Так как при адиабатическом процессе dQ=0, то dA =– dU. Первое начало термодинамики будет иметь вид
dU + dA=0 или С V dT + PdV=0.
Откуда следует, что при адиабатическом процессе работа совершается за счет изменения внутренней энергии.
Например, если открыть ниппель у автомобильного колеса, то выходящий воздух можно рассматривать как адиабатическое расширение. Работа по расширению воздуха происходит за счет уменьшения внутренней энергии, что приведет к охлаждению воздуха и ниппель станет холодным.
Степени свободы
Согласно молекулярно–кинетической теории внутренняя энергия, которая обусловлена движением молекул как поступательным, так и вращательным, определяется (10), где i– число степеней свободы.
Числом степеней свободы i называется число независимых координат, полностью определяющих положение молекулы в пространстве.
В случае жесткой связи например:
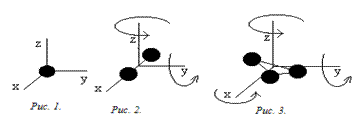
1. У одноатомной молекулы только три степени свободы поступательного движения, i=3 (для атома как материальной точки не учитывается вращательное движение); (рис.1).
2. У двухатомной молекулы три степени свободы поступательного движения и две степени свободы вращательного движения, i=5 (рис.2);
3. У трехатомной молекулы три степени свободы поступательного движения и три степени свободы вращательного движения; i=6 (рис. 3).
Из (10), (11) и (12) можно вычислить внутреннюю энергию и теплоемкости газа, а по формуле (1) определить адиабатическую постоянную g.
1. Для одноатомного газа i=3
;
;
.
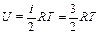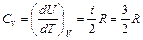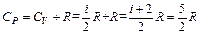Адиабатическая постоянная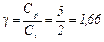 
.
2. Для двухатомного газа i=5 и аналогично предыдущему получим
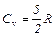
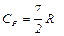
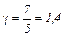
3. Для трехатомного газа i=6
; 
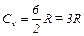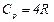
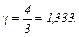
В общем случае:
; 
; 
.
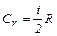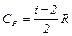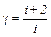4. Теория метода и описание установки
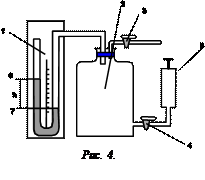
Экспериментальная установка состоит из стеклянного баллона 2 (рис.4), соединенного с манометром 1 и насосом 5. Посредством крана 3 баллон 2 может быть соединен с атмосферой. Давление в манометре h определяется по разности уровней жидкости левого колена 6 и правого колена 7.
|
Для накачки воздуха в баллон надо открыть кран 4 и закрыть кран 3.Если при помощи насоса накачать в баллон некоторое количество воздуха, а затем закрыть кран 4, то давление и температура воздуха внутри баллона повысятся (внешними силами совершается работа по сжатию газа). Выждав определенное время (2–3 мин), вследствие теплообмена воздуха с окружающей средой температура воздуха, находящегося в баллоне, сравняется с комнатной температурой t1, а давление при этом слегка понизится, о чем можно судить по показанию манометра.
Давление, установившееся в баллоне,
p1=H + h1,
где Н – атмосферное давление, h1 – атмосферное давление, измеряемое разностью уровней жидкости в манометре 1.
Таким образом, состояние воздуха внутри баллона, которое назовем первым состоянием, будет характеризоваться параметрами: P1=H + h1; v ; Т1. Этому состоянию газа соответствует точка 1 рис.5. Затем открываем на короткое время кран 3 (рис.4), соединяем баллон с окружающей средой. Этот процесс расширения можно считать адиабатическим.
Давление в сосуде установится равным атмосферному P 2 = Н, температура понизится до Т2<Т1, а объем будет равен V2. Следовательно, в конце адиабатического процесса у воздуха в баллоне будут параметры H ; V 2 ; T 2(T 2 < T 1) (рис.5 точка 2).
Переход из первого состояния во второе является адиабатическим, к такому переходу применим уравнение Пуассона
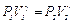. (14)
Через три–четыре минуты после закрытия крана воздух в баллоне нагреется изохорически до комнатной температуры t 1 , а давление повысится до Р3 = H + h 2 (точка 3 на рис.5) h 2–разность уровней в манометре, когда температура в баллоне стала равной комнатной. Сравнивая конечное состояние «3» с первоначальным состоянием «1», видим, что они принадлежат одной и той же изотерме.
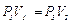(15)
Возведем (15) в степень g, получим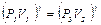 
и разделим его на (14): 
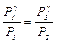прологарифмируем – 
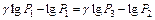, отсюда 
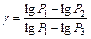. Принимая во внимание, что Р1= H + h 1 , P 2 = H , P 3 = H + h 2, т.е. давления мало отличаются друг от друга, разность логарифмов можно принять пропорциональной разностям самих давлений и
,
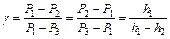откуда
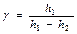. (16)
Последняя формула – рабочая.
Порядок выполнения работы
1. Осторожно (чтобы не выплеснуть жидкость из манометра) накачайте в баллон воздух, так чтобы разность уровней в коленах манометра составляла 80–100 мм. Так как при нагнетании воздуха в баллон температура его возрастает, то перед тем как снять показание давления, надо выждать одну минуту, пока через стенки баллона температура воздуха в нем не выравняется с температурой окружающей среды. Процесс выравнивания температуры можно заметить по небольшому изменению уровней жидкости в коленах манометра, которое прекращается, как только произойдет выравнивание температур. В это время снимите значение h1, равное разности уровней.
2. Проведите над газом процесс адиабатического расширения (помните, что он должен пройти без теплообмена с окружающей средой). Для этого откройте кран 3, при этом слышится характерное шипение. Как только оно прекратится, кран следует быстро закрыть. Расширяясь воздух в сосуде охладится.
3. Предоставьте возможность газу в баллоне через стенки нагреться до температуры окружающей среды, т.е. до первоначальной температуры t1. При нагревании газа давление в баллоне повышается, и уровень жидкости в коленах манометра изменяется. После выравнивания температуры снимите значение h2.
4. Подставьте в рабочую формулу значения h 1 и h 2 вычислите значение g. Опыт повторите 5 – 7 раз.
Все полученные в результате опытов и вычисленные данные сводят в таблицу.
| № опыта | h1 | h2 | g | D g |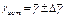 
|
| Средние значения |
Расчет погрешности
Относительная ошибка измерения γ
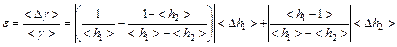
Абсолютная ошибка:
< Δγ > = < γ >. ε
Окончательный результат записывается в виде: γист = <γ> ± < Δγ >
Задачи
1. Найти для кислорода отношение удельной теплоемкости при постоянном давлении к удельной теплоемкости при постоянном объеме.
Ответы:1) 1,45; 2) 1,33; 3) 1,67; 4) 1,40; 5) 1,30.
2. Для некоторого двухатомного газа удельная теплоемкость при постоянном давлении 14,7.103 Дж/кгК. Чему равна молярная масса этого газа?
Ответы:1) 32.10–3 кг/моль; 2) 24.10–3 кг/моль; 3) 4.10–3 кг/моль; 4) 2.10–3 кг/моль; 5) 28.10–3 кг/моль.
3. По какой формуле следует определять количество теплоты, необходимое для нагревания определенной массы вещества?
Ответы:1) Q =∆ U +∆ A; 2) Q = cm ∆ T; 3) Q = λm; 4) Q = rm ( t 2 – t 1 ); 5) Q =∆ λ ∆ T.
4. Газу передано 200 Дж теплоты и при этом он совершил работу 200 Дж против внешних сил. Каково изменение внутренней энергии?
Ответы:1) 0 Дж; 2) 400 Дж; 3) 200 Дж; 4) 100 Дж; 5) 800 Дж.
5. Если в некотором процессе газ совершил работу, равную 5 кДж, а его внутренняя энергия уменьшилась на 5 кДж, то такой процесс является:
Ответы:1) изотермическим; 2) изобарическим; 3) такой процесс невозможен; 4) изохорическим; 5)адиабатическим.
6. При увеличении объема идеального газа в 2 раза и повышении его абсолютной температуры в 4 раза давление газа:
Ответы:1) увеличится в 8 раз; 2) увеличится в 2 раза; 3) уменьшится в 2 раза; 4) увеличится в 4 раза; 5) уменьшится в 4 раза.
7. Может ли газ нагреться или охладиться без теплообмена с окружающей средой? Как это происходит?
Ответы: 1) при изотермическом процессе; 2) изохорическом процессе; 3) адиабатическом процессе; 4) изотермическом процессе; 5) такой процесс невозможен.
8. Газ при адиабатическом процессе совершил работу 200 МДж. Как изменилась ее внутренняя энергия? Что произошло с газом? Охладился, нагрелся?
Ответы: 1) на 300 МДж, нагрелся; 2) на 100 МДж, охладился; 3) на 450 МДж, охладился; 4) на 200 МДж, газ охладился; 5) осталась без изменения, газ не нагрелся и не охладился.
9. При передаче газу количества теплоты 17 кДж он совершил работу равную 50 кДж. Чему равно изменение внутренней энергии? Охладился газ или нагрелся?
Ответы: 1) увеличилась на 33 кДж, нагрелся; 2) уменьшилась на 17 кДж, охладился; 3) увеличилась на 50 кДж, нагрелся; 4) уменьшилась на 33 кДж, охладился; 5) не изменилась, газ не нагрелся, не нагрелся.
Контрольные вопросы
1. Цель работы.
2. Что такое молярная и удельная теплоемкости ?
3. Какие и сколько теплоемкостей различают у газа ?
4. Какая теплоемкость больше и почему? Уравнение Р. Майера.
5. Формулы CV и CP через число степеней свободы.
6. Сколько и какие степени свободы у одно-, двух- и трех- атомного газа?
7. Записать показатель адиабаты g= CP / CV через число степеней свободы.
8. Каким способом вы определили CP / CV.
9. Какие процессы при этом осуществлялись над газом ?
10. Поясните изохорический, изобарический, изотермический и адиабатический процессы: процессы, анализ, графики.
11. Как изменялись параметры газа: P , V , T в данной работе ?
12. Вывод рабочей формулы.
Литература
1. Детлаф А. А., Яворский Б. М. Курс физики, М.: Высшая школа, 1989, с.97–103.
2. Савельев. Курс общей физики. М.: Наука, т.1, 1989, т.1, c.231–241, 245–246.
3. Трофимова Т. И. Курс физики, М.: Высшая школа, 2002, с.100–107.
Лабораторная работа 1.13
Определение приращения энтропии при плавлении олова
Краткая теория
Термодинамика – раздел физики, в котором изучается связь между различными макроскопическими величинами и энергетическими характеристиками системы. Особенностью термодинамического подхода является отсутствие представлений о внутреннем строении системы, что делает выводы термодинамики наиболее общими, хотя и более формальными.
Первое начало термодинамики