Наименьшее расстояние d , на которое приблизятся друг к другу центры молекул при столкновении, называется эффективным диаметром молекул.
На расстоянии d вся кинетическая энергия молекул полностью расходуется на совершение работы против сил отталкивания. Расстояние d тем меньше, чем больше кинетическая энергия молекул, т.е. чем выше температура газа.
3. Одним из явлений, позволяющих определить среднюю длину свободного пробега молекул газа, является внутреннее трение в газе.
Внутреннее трение возникает между слоями газа (или жидкости), движущимися с разными скоростями.
Рассмотрим газ, движущийся в трубке с малым диаметром. Ламинарное движение газа по трубке можно представить в виде слоев, в которых скорости газа постоянны. Вблизи поверхности трубки, вследствие взаимодействия молекул газа с поверхностью, скорость молекул газа вдоль трубки (скорость слоя газа) наименьшая и увеличивается по мере приближения к центру. Распределение скоростей по диаметру трубки можно представить в виде параболы.
Вследствие хаотического движения молекула переходит из одного слоя в другой, перенося с собой импульс (количество движения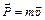 
). В результате, между слоями возникает сила внутреннего трения, направленная противоположно скорости слоев, и стремящаяся выравнить скорости слоев (молекула из быстрого слоя пытается ускорить, а из медленного – замедлить слой, в который она перейдет).
Сила внутреннего трения пропорциональна градиенту скорости и площади трущихся слоев и направлена против движения слоев
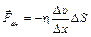. (4)
Градиентом скорости называется изменение скорости на каждой единице длины в направлении, перпендикулярном скорости
.
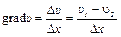h – коэффициент внутреннего трения, равный силе внутреннего трения между слоями единичной площади при градиенте скорости, равном единице.
4. Из молекулярно–кинетического рассмотрения явления внутреннего трения вытекает, что коэффициент внутреннего трения в газе равен
,
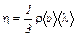где r – плотность газа.
Именно эта формула позволяет определить среднюю длину свободного пробега <l>:
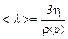. (5)
Выразим h,r, <υ> через известные параметры и величины, которые можно измерить, и рассчитаем <l>:
а) для нахождения h воспользуемся формулой Пуазейля, определяющей объем газа V, протекающего через трубку длинной ℓ, радиусом r, за время t, при перепаде давления на ее концах, равном Dp:
;
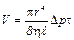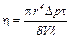. (6)
б) средняя скорость молекул газа из молекулярно–кинетической теории выражается:
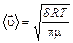. (7)
в) плотность газа r найдем из уравнения состояния идеального газа (Менделеева–Клапейрона)
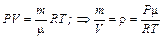. (8)
Подставляя (6,7,8,) в (5) получим:
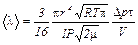. (9)
Соберем все постоянные в одну и вычислим ее:
.
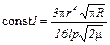Окончательно получим:
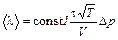. (10)
const 1 – табличное значение.
Как видно из (10), задача свелась к определению величин V , t, T, Dp. Dp–перепад давления на концах трубки.
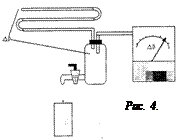
Перепад давления можно создать за счет выливания жидкости из баллона, который соединен с одним из концов трубки (капилляра) (рис.4).
Когда кран закрыт, давление воздуха внутри баллона и снаружи одинаковое, перепад давления на концах трубки капилляра равен нулю. Если кран открыть полностью, то вода начнет вытекать, давление газа внутри баллона начнет уменьшаться из–за увеличения объема газа, на концах трубки появится перепад давления. Признаком установившегося перепада давления является капание воды с полностью открытого крана. В этом случае можно считать, что количество прошедшего воздуха через трубку равно количеству воды, вытекшей из баллона.
Выполнение работы
1. Откройте кран, подождите пока вода не начнет капать и не установится перепад давления Dp (по манометру).
2. Подставьте под капающую воду мензурку (при полностью открытом кране), одновременно включите секундомер.
3. Измерьте объем вытекшей воды и время, все данные занесите в таблицу.
4. После того как найдете среднюю длину свободного пробега, определите эффективный диаметр по формуле (3):
.
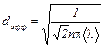Концентрацию молекул воздуха определим из выражения
,
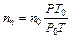где Р0, T0 – давление и температура при нормальных условиях, T0 = 273,15 К, Р0=1,0132×105 Па = 760 мм рт.ст.; n0 – число Лошмидта – число молекул, находящихся в 1 см3 идеального газа при нормальных условиях, оно равно: n 0 = 2,687 1019 см–3, P , T –давление и температура, при которых протекает опыт.
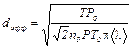. (11)
Окончательно формула для расчета эффективного диаметра :
;
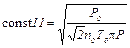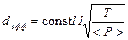. (12)
Занесите данные в таблицу
| № | t,с | V,м3 | Dp,Па | Т,К | l | dэфф |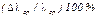 
| lист | d ист |
| 3 | |||||||||
| Среднее значение | |||||||||
Расчет погрешности
Относительная ошибка длины свободного пробега: Относительная ошибка эффективного диаметра
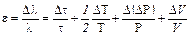Абсолютная ошибка:
Δλ = ε λ,
| 
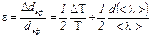Абсолютная ошибка:
Δd эф = ε d эф
|
Δτ = 0,01 с; ΔТ = 0,50; ΔР = 20 ед.давл; ΔV=10–6 м3
Задачи
1. Определите среднюю длину свободного пробега <λ> молекул кислорода, находящегося при температуре 00С, если среднее число столкновений, испытываемых молекулой в 1 с, равно 3,7.109.
Ответы:1) 6,5.10–8 м; 2) 4,52.10–8 м; 3) 11,5.10–8 м; 4) 15.10–8 м; 5) 3.10–8 м.
2. При каком давлении средняя длина свободного пробега молекул водорода равна 2,5 см, если температура газа равна 670 С? Диаметр молекул водорода 0,28 нм.
Ответы:1) 1,32 Па; 2) 0,77 Па; 3) 0,539 Па; 4) 2,37 па; 5) 0,428 Па.
3. Определите длину свободного пробега молекул углекислого газа при нормальных условиях, если при этих условиях его плотность ρ=2 кг/м3, а коэффициент внутреннего трения 14,9.10–6кгм/с.
Ответы:1) 8,32.10–8м; 2) 3,52.10–10м; 3) 7,42.10–8м; 4) 6,20.10–8м; 5) 3,90.10–8м.
4. Как связаны давление идеального газа Р, концентрация его молекул и его температура?
Ответы:1) Р=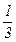 
nкТ; 2) Р= 
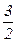nкТ; 3) Р=nкТ; 4) Р= 
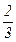nкТ; 5) Р=кТ.
5. Средняя длина свободного пробега <λ1> молекул водорода при нормальных условиях составляет 0,1 мкм. Определите среднюю длину свободного пробега при давлении 0,1 мПа, если температура остается постоянной.
Ответы:1) 52 м; 2) 15,3.10–2 м; 3) 101 м; 4) 1,34 м; 5) 7,2.10–4 м.
6. Средняя длина свободного пробега <λ> молекулы углекислого газа при нормальных условиях равна 40 нм. Определить среднее число соударений <z>, которые испытывает молекула в 1 с.
Ответы:1) 1010 с–1; 2) 3,1.109 с–1; 3) 7,52.109 с–1; 4) 9,05.109 с–1; 5) 8,33.109 с–1.
Контрольные вопросы
1. Дать определение средней длины свободного пробега и эффективного диаметра молекул.
2. Какое физическое явление положено в основу работы? Запишите уравнение Ньютона.
3. Каков физический смысл коэффициента внутреннего трения.?
4. Что такое градиент скорости и куда он направлен?
5. Почему вода из баллона сначала вытекает, а затем капает?
6. Объяснить формулу Пуазейля.
7. Подробно вывести рабочую формулу.
Литература
1. Савельев И. В. Курс общей физики, т. 1. М.: Наука, 1989. с.269–274, 285–287.
2. Трофимова Т. И. Курс физики. М.: Высшая школа, 2002, с.91–96
3. Детлаф А. А., Яворский Б. М. Курс физики, М.: Высшая школа, 1989, с.114–119.
Лабораторная работа 1.11