Определение средней длины свободного пробега и эффективного диаметра молекул воздуха
Приборы и принадлежности: особая установка, смонтированная на
установке, мензурка, секундомер,
манометр.
Молекулы газа движутся хаотически, сталкиваются друг с другом и со стенками сосуда.
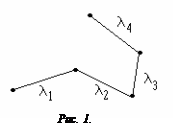Расстояние, проходимое молекулой между двумя последовательными соударениями, называется длиной свободного пробега l (рис. 1) .
На длине свободного пробега молекула движется равномерно и прямолинейно.
Среднее расстояние, проходимое молекулой между двумя последовательными соударениями, называется средней длиной свободного пробега < l >
Оно равно
.
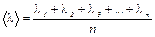Чтобы найти среднюю длину свободного пробега, нужно расстояние, пройденное молекулой за единицу времени (т.е. среднюю скорость молекулы <υ>), разделить на число столкновений <Z > за единицу времени:
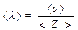. (1)
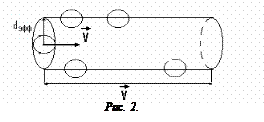Найдем Z, считая, что все молекулы, кроме одной, покоятся, а единственная молекула движется по оси цилиндра. За единицу времени она столкнется со всеми молекулами, находящимися внутри цилиндра радиусом r, равным эффективному диаметру dэфф молекулы газа и длиной, равной скорости молекулы.
Поэтому число столкновений в единицу времени определится числом молекул, которые окажутся внутри этого цилиндра. Число столкновений в единицу времени <Z > равно произведению концентрации n на объем цилиндра:
,
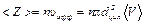где <υ> – средняя скорость молекулы. По построению она равна длине цилиндра. Если считать, что остальные молекулы тоже двигаются, то в расчеты достаточно добавить поправочный коэффициент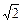 
. Тогда окончательно получим:
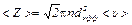, (2)
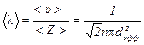. (3)
У воздуха при нормальных условиях (t=0 0С или T=273 К, давление Р=105 Па, что соответствует нормальному давлению 760 мм рт. ст.), средняя скорость – 447 м/с, число молекул в единице объема – 1025 в 1 м3, средняя длина свободного пробега – 60 ×10–9 м, число столкновений в 1 секунду 1,8×108 раз, эффективный диаметр молекулы составляет 3×10–10 м.
Средняя длина свободного пробега обратно пропорциональна давлению газа (см формулу 3), давление газа пропорционально концентрации n молекул газа (p = nkT), и если <l>, согласно (3), обратно пропорциональна концентрации n, то, следовательно, и обратно пропорциональна p.
2. Рассмотрим теперь понятие эффективного диаметра молекулы.
Между молекулами любого вещества одновременно действуют силы взаимного притяжения и отталкивания. Они называются силами молекулярного взаимодействия и имеют электрическое происхождение, поскольку ядра и электроны соседних молекул испытывают электрические силы отталкивания и притяжения. Именно силы межмолекулярного взаимодействия определяют характер теплового движения молекул твердых, жидких и газообразных тел.
В газах силы притяжения между молекулами не могут преодолеть силы отталкивания, и молекулы разлетаются во все стороны, занимая весь объем сосуда, в котором находится газ. Газы не имеют определенного объема и формы и легко сжимаются под действием внешнего давления. При столкновениях молекулы приближаются друг к другу на расстояние r=10–10 м между их центрами. На этом расстоянии силы отталкивания резко возрастают за счет перекрытия их электронных оболочек (сила отталкивания носит квантовый характер и поэтому растет значительно быстрее электрической силы притяжения). Действие сил отталкивания приводит к такому же результату, как и столкновение молекул – молекулы отталкиваются друг от друга.