Баллистический маятник

Дата: 2025-04-30; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Цель работы: изучение движения крутильного маятника под действием короткого импульса внешней силы и определение скорости пули методом крутильного маятника.

Оборудование: лабораторная установка (рис. 1).

Материал для изучения: крутильные колебания; уравнение моментов.

Теоретическое введение

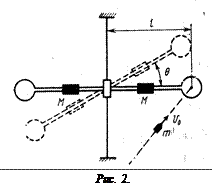
Основным элементом лабораторной установки является крутильный маятник (рис. 2). При попадании в него выпущенной стреляющим устройством «пули» маятник начинает вращаться вокруг вертикальной оси. Максимальный угол q_max маятника из положения равновесия связан со скоростью υ₀ пули соотношением

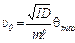, (1)

где m – масса пули, ℓ– прицельное расстояние (рис. 1), I – момент инерции маятника, D – постоянная момента упругих сил.

Для экспериментального определения скорости пули удобно преобразовать соотношение (1) так, чтобы в него входили непосредственно измеряемые на опыте величины. Сначала воспользуемся формулой для периода колебаний Т слабо затухающего крутильного маятника и исключим неизвестную величину D

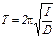. (2)

В результате получим

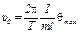. (3)

Согласно теореме Гюйгенса – Штейнера, момент инерции маятника

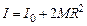, (4)

где 2М – масса двух имеющихся на маятнике подвижных грузов,

R – расстояние от центра масс каждого из этих грузов до оси вращения.

Подставляя это выражение в (3), получаем следующую формулу для определения скорости пули:

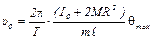. (5)

Измерения

Соотношение (1), использовавшееся при выводе выражения (5), было получено для идеализированной модели, а именно, предполагалось, что выполнены следующие условия:

1) колебания маятника являются незатухающими;

2) время τ соударения пули с маятником мало по с равнению с периодом колебаний:

τ << T (6)

(баллистический режим).

Поэтому прежде всего необходимо выяснить, обеспечивается ли выполнение этих условий для имеющейся лабораторной установки.

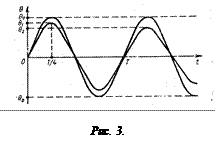Сначала обсудим первое из них. Отклонив маятник из положения равновесия, легко убедиться, что амплитуда его колебаний довольно быстро уменьшается. Следовательно, модель незатухающих колебаний не является точной и применение полученной в рамках этой модели формулы (5) может привести к систематической погрешности в определении скорости пули.

Оценим эту погрешность, для чего сравним графики зависимости амплитуды незатухающих и затухающих колебаний маятника от времени. Будем считать, что в обоих случаях маятник выведен из положения равновесия в момент времени t = 0 с одинаковой начальной скоростью (рис. 3).

Как видно из рисунка, пренебрежение затуханием приводит к заниженному значению скорости пули. Действительно, в формулу (5) подставляется измеренная величина θ₁ = θ_max, а она меньше, чем соответствующая той же начальной скорости амплитуда незатухающих колебаний θ₀. Следовательно, при определении θ_max возникает систематическая погрешность, равная

Δθ_сист = θ₁ – θ₀.

Для оценки заметим, что она накапливается за четверть периода колебаний, т.е. за время 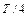. Уменьшение амплитуды колебаний за полный период Т можно измерить непосредственно:

Δθ = θ₂ – θ₁,

где θ₁ и θ₂ – соответственно углы первого и второго максимального отклонения маятника после попадания в него пули. Считая зависимость амплитуды затухающих колебаний от времени приблизительно линейной (для этого нужно, чтобы затухание за период было мало), находим

.

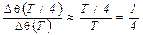Следовательно,

,

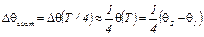т.е.

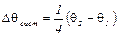. (7)

Если θ₁ и θ₂ совпадают в пределах точности, с которой измеряется угол отклонения θ маятника, то Δθ_сист, очевидно, можно пренебречь и модель незатухающих колебаний справедлива.

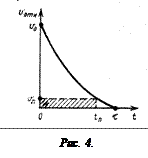
Попробуем теперь оценить τ (τ – время соударения пули с маятником). Построим качественно график зависимости скорости пули от времени относительно маятника (рис. 4.)

Непосредственно перед соударением маятник покоится, а скорость пули равна υ_о: значит, их начальная относительная скорость υ_отн (0) = υ_о. В конце удара, т.е. при t = τ, по определению, υ_отн (τ) = 0.

Естественно считать, что в течение удара скорость υ_отн постепенно (монотонно) убывает от υ_о до нуля. Без проведения специальных измерений ничего более определённого сказать о зависимости υ_отн от t нельзя: для этого необходимо заранее знать закон взаимодействия между соударяющимися телами. Нам же надо лишь приближенно оценить τ.

Пусть t_n – момент, когда относительная скорость пули уменьшается по сравнению с начальной в n раз:

.

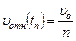Из рис.3 видно, что полное перемещение пули в материале маятника

,

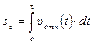равное полной площади под кривой υ_отн (t), заведомо превышает площадь заштрихованного прямоугольника:

.

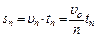При достаточно больших значениях n, например при n > 10, можно считать, что t_n мало отличается от времени соударения τ, и положить τ ≈ t_n. Тогда получаем неравенство

,

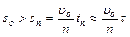которое позволяет получить оценку τ:

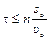. (8)

Величины, стоящие в правой части неравенства (8), определяются на опыте. В лабораторной установке глубина проникновения пули в маятник s_о ≤ 0,5 см, а скорость пули υ_о ≥ 1 м ∕с.

Следовательно, 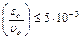с и при n = 10 получаем для τ оценку сверху: τ≤0,05 с.

Так как период колебаний маятника Т ≈ 1 с, то можно считать, что равенство (6) в этих условиях выполняется.

Примечание. Выбор величины n = 10 может показаться произвольным. Однако при 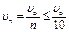практически можно считать, что удар действительно «закончился», так как к этому моменту кинетическая энергия пули

,

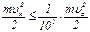т.е. составляет всего лишь примерно 1 % её первоначальной кинетической энергии.

Выясним теперь, как определить в рабочей формуле неизвестную величину I_о. Для этого запишем период колебания маятника в виде

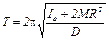. (9)

Таким образом, Т зависит от расстояния R центров подвижных грузов M от оси вращения.

Установив грузы M на некотором расстоянии R₁ от оси вращения, можно определить период колебаний T₁ маятника. Сместим грузы M в другое положение R₂ и снова измерим период колебаний T₂ маятника. Так как [см. (9)]

,

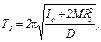
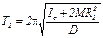то, исключая из этих равенств D, находим

.

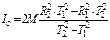Для уменьшения погрешности, с которой определяется величина I_о, расстояния R₁ и R₂ следует взять заметно отличающимися друг от друга. Лучше всего взять R₁ возможно ближе к оси вращения, а R₂ – на максимальном расстоянии от неё.

После того как найдено I_о, скорость пули может быть определена из формулы (5) по известным значениям массы m пули, масс M грузов и измеряемым на опыте значениям периода колебаний T, прицельного расстояния l, расстояния R и угла отклонения θ_max маятника.

Для повышения точности измерений рекомендуется устанавливать грузы M на небольшом расстоянии R от оси маятника, чтобы угол отклонения θ_max маятника был как можно больше.

Задание

1. Установите подвижные грузы M на минимальном расстоянии от оси вращения и, сделав 2–3 выстрела, определите приближенно угол отклонения θ₁ маятника при попадании в него пули.

2. Оцените по формуле (7) Δθ_сист. Для этого отклоните маятник из положения равновесия на угол θ₁, отпустите без толчка и измерьте

амплитуду θ₂ второго отклонения маятника в ту же сторону. Измерения повторите три раза и найдете среднее арифметическое значение θ₂. Результате измерений занесите в табл. 1.

Таблица 1

θ1	θ2,1	θ2,2	θ2,3		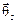Δθсист	Δθо

Сравните найденное значение Δθ_сист с погрешностью Δθ_о измерений угла по шкале устройства (Δθ_о равно половине цены деления шкалы).

3. Определите Т_о. Для этого измерьте периоды колебаний маятника Т₁ и Т₂ при двух различных положениях R₁ ≈ R_min и R₂ ≈ R_max пар подвижных грузов M. Результаты измерений занесите в табл. 2

Таблица 2

R 1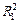

ΔR 1

R 2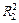

ΔR 2

T 1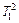

T 2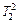

M

Io

ΔIo

4. Установив на расстоянии R ≈ R_min грузы M, измерьте отклонение маятника θ = θ_max и прицельное расстояние l в серии из четырех выстрелов. Результаты измерений занесите в табл. 3.

Таблица 3

l 1

l 2

L 3

l 4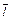

Δl

θ1

θ2

θ3

θ4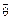

Δθ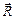

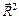
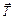
Δ T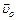

Δυо

Пользуясь соотношением (5), определите скорость пули.

Можно ли утверждать, что скорость пуль в серии выстрелов одинакова в пределах точности измерений или имеется разброс в скорости пуль от выстрела к выстрелу?

5. Измерьте приближенно глубину S_о, на которой пуля застревает при попадании в маятник. Оцените по формуле (8) время соударения τ пули с маятником, полагая в (8) n = 10. Убедитесь в том, что неравенство (6) в условиях опыта действительно выполняется.

Задачи

1. Два тела (m₁=3 кг, m₂=2 кг), двигавшиеся навстречу друг другу (υ ₁=2 м/c, υ₂=3 м/с) после неупругого удара:

Ответы: 1) будут двигаться вправо со скоростью 2 м/с; 2)будут двигаться вправо со скоростью 1 м/с; 3) остановятся; 4) будут двигаться влево со скоростью 1 м/с; 5) будут двигаться со скоростью 2 м/с.

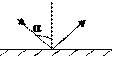
2. Чему равен модуль изменения импульса тела массой m при абсолютно упругом ударе о

некоторую плоскую поверхность, как показано на рисунке?

Ответы: 1) mυ cosα; 2) 2 mυ cosα; 3) mυ sinα; 4) 2 mυ sinα; 5) mυ(cosα–sinα)

3. Тело массой 0,2 кг падает с высоты 1 м с ускорением 8м/с. Найти изменение импульса.

Ответы:1) 10,3 кг^.м/с; 2) 0,6 кг^.м/с; 3) 0,8 кг^.м/с; 4) 3,2 кг^.м/с; 5) 1,2 кг^.м/с.

4. Два шара массами 6 кг и 4 кг движутся вдоль одной прямой со скоростями 8 м/с и 3 м/с. С какой скоростью они будут двигаться после абсолютно неупругого удара, если первый шар догоняет второй?

Ответы:1) 12,7 м/с; 2) 10 м/с; 3) 5,7 м/с; 4) 6 м/с; 5) 8,0 м/с.

5. Снаряд массой 100 кг, летящий горизонтально вдоль железнодорожного пути со скоростью 500 м/с, попадает в вагон с песком массой 10 т и застревает в нем. Найти скорость вагона, если он двигался со скоростью 10 м/с навстречу снаряду

Ответы:1) 7,62 м/с; 2) 12,8 м/с; 3) 9,35 м/с; 4) 4,54 м/с; 5) 5,76 м/с.

6. Молекула массой 5^.10^–26 кг, летящая со скоростью 500 м/с, упруго ударяется о стенку под углом 30⁰ к перпендикуляру. Найти импульс силы, полученный стенкой при ударе:

Ответы:1) 7,26^.10^–23 Н^.с; 2) 9^.10^–22 Н^.с; 3) 2,34^.10^–22 Н^.с; 4) 6,8^.10^–22 Н^.с; 5) 4,32^.10^–23 Н^.с.

Контрольные вопросы

1. Выведите формулу (1): .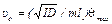

2. На основании полученных вами данных оцените постоянную момента упругих сил D.

3. По экспериментальным результатам оцените кинетическую энергию маятника: .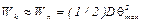

4. Оцените, какая часть кинетической энергии пули при ударе переходит в теплоту.

Литература

1. Каленков С. Г., Соломахо Г. И. Практикум по физике. М.: 1990, Высшая школа.

2. Сивухин Д. В. Общий курс физики. М.:1989, Механика, т.1.

3. Детлаф А. А., Яворский Б. М. Курс физики М.: 1989.

Лабораторная работа 1.9

Маятник Максвелла

Цель работы: необходимо определить момент инерции диска,

линейную скорость вертикального падения маятника,

линейное ускорение маятника.

Приборы и принадлежности: маятник Максвелла, секундомер,

линейка.

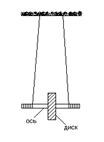
Маятник Максвелла представляет собой диск, подвешенный на двух невесомых и нерастяжимых нитях.

Масса диска m = 407 г~ 0,41 кг,

радиус оси r = 2,5. 10 ^–3 м,

радиус диска R = 0,1 м.

Нити невесомы и нерастяжимы.

g₀ = 9,81 м/с² ~ 10 м/с² – ускорение свободного падения на поверхность земли “h = 0”.

Выполнение работы

Закручиваем нити маятника на ось и поднимаем его на высоту “h”. Тогда маятник будет иметь потенциальную энергию

E_n = m g ₀ h . (1)

Опустив маятник будем наблюдать превращение потенциальной энергии маятника в кинетическую энергию вращательного движения

E _вр = I ω² / 2 (2)

и в кинетическую энергию поступательного движения

E _пос = mυ ² / 2, (3)

если трением пренебречь, то на основе закона сохранения и превращения энергии можно считать

m g h = I ω² / 2 + m υ ² / 2. (4)

Беря производную от (4) по времени, имеем:

mg 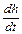= 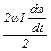+ 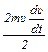, (5)

а т.к. 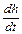= υ; ω = ; = ,

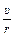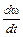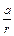то имеем

m g υ = m υ a + 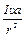, (6)

откуда находим

I a = m g r² – m a r² (7)

или

I = m r² ,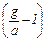

так как h = 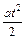, то a =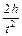

и тогда получаем рабочую формулу: I = m r²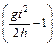

υ = a t =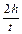

Данные заносим в таблицу:

№	h	t	m	r	υ	a	I	Δ I	Δ I/I*100%	I ист 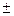=I ср Δ I ср
Сред.знач.

Задачи

1. Какой вид имеет период колебаний пружинного маятника?

Ответы:

.

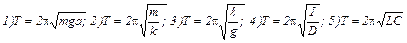2. Какой вид имеет период колебаний математического маятника?

Ответы:

.

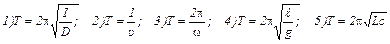3. Длину математического маятника увеличили в 4 раза. Как изменился период колебаний?

Ответы: 1) остался без изменения; 2) увеличился в 4 раза; 3) увеличился в 2 раза; 4) уменьшился в 4 раза.

4. Масса тонкого кольца увеличилась в 2 раза. Во сколько раз изменился момент инерции кольца относительно оси, проходящей через центр масс перпендикулярно плоскости кольца?

Ответы:1) не изменился; 2) уменьшился в 2 раза; 3) увеличился в 2 раза; 4) увеличился в 4 раза.

5. Масса диска увеличилась в 2 раза и в 2 раза увеличился радиус диска. Во сколько раз изменился момент инерции относительно оси, проходящей через центр масс, перпендикулярно плоскости диска?

Ответы: 1) не изменился; 2) увеличился в 2 раза; 3) увеличился в 4 раза; 4) увеличился в 8 раз; 5) увеличился в 16 раз.

Контрольные вопросы:

1. Какой закон лежит в основе вывода рабочей формулы?

2. Можно ли считать колебания маятника Максвелла гармоническими?

3. Физический смысл момента инерции.

4. В каких единицах измеряется момент инерции?

5. Будет ли совершать колебания маятник Максвелла в состоянии невесомости?

Литература

1. Бондарев Б. В., Спирин Г. Г, Калашников Н. П. Курс физики. М.: Курс общей физики, 2003, т.1, с.186, 192.

2. Савельев И. В. Курс общей физики, т. 1. М.: Наука, 1989.

3. Трофимов a Т. И. Курс физики. М.: Высшая школа, 2002.

Лабораторная работа 1.10