Контрольные вопросы
1. Закон сохранения энергии. Закон сохранения полной механической энергии. Какой из этих законов не выполняется в лабораторной работе и почему ?
2. Консервативные и диссипативные силы. Примеры этих сил.
3. Цель работы.
4. Физический смысл момента инерции.
5. Момент инерции материальной точки, твердого тела.
6. Размерность момента инерции.
7. Применить закон сохранения энергии к лабораторной установке.
8. Вывести рабочую формулу.
9. Угловая скорость. Угловое ускорение. Вектор угловой скорости и ускорения.
Литература
1. Савельев И. В. Курс общей физики, т. 1. М.: Наука, 1989. с. 79–81, 103–108.
2. Трофимова Т. И. Курс физики. М.: Высшая школа, 2002, с.27–29, 34–36.
3. Бондарев Б. В., Спирин Г. Г., Калашников Н. П. Курс физики. М.: 2003, т.1,
с.128–130.
Лабораторная работа 1.3
Определение модуля упругости методом изгиба
Цель работы: определить модуль упругости стержня методом изгиба.
Приборы и принадлежности : две опоры, испытуемые стержни, набор
грузов, отсчетный микроскоп.
Краткая теория
Сила характеризует воздействие одного тела на другое. В результате этого воздействия тело может получить ускорение или деформироваться.
Деформацией твердого тела называется изменение его размеров и объема.
Силы можно разделить на две категории: 1 – силы, обусловленные взаимодействием непосредственно соприкасающихся тел (удар, давление, растяжение, трение и др); 2 – силы, связанные с особой формой материи, называемой полем и осуществляющей взаимодействие между телами без их соприкосновения (силы гравитации, электрические, магнитные, ядерные).
При деформации твердого тела, например металла, в нем происходят очень сложные явления, которые еще недостаточно исследованы.
Металлы представляют собой совокупность хаотически расположенных и различно ориентированных друг относительно друга мелких кристалликов. Вследствие этого упругие свойства металла по различным направлениям одинаковы и металлы являются изотропными телами.
Деформации в металле можно разделить на упругие и пластические.
Упругими деформациями называются деформации, при которых после прекращения действия силы, вызывающей деформацию, тело принимает первоначальные размеры и форму.
Пластические деформации возникают тогда, когда силы, действующие на тело, перешли определенный предел, называемый пределом упругости и после прекращения действия силы тело не восстанавливает свои размеры и форму. Тело остается деформированным, в нем возникают остаточные деформации. Если после возникновения остаточных деформаций мы продолжаем увеличивать внешнюю силу, то наблюдается разрушение тела.
Деформацию металла можно представить так. В зоне упругих деформаций кристаллики металла изменяют свою форму, не сдвигаясь и не разрушаясь. После снятия действия силы они возвращаются в прежнее состояние под действием атомарных сил, действующих между кристалликами. Таким образом, в упругодеформированном теле возникают внутренние силы, которые уравновешивают внешние силы, приложенные к телу.
Физическая величина s , численно равная упругой силе dF упр , приходящейся на единицу площади поперечного сечения тела dS , называется механическим напряжением:
.
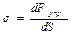Таким образом, напряжение характеризует внутренние силы, возникающие между атомами в кристаллической решетке при деформации тела.
Напряжение называется нормальным, если сила dF упр направлена перпендикулярно к площади dS, s 0 = dF / dS и касательным, если она направлена по касательной к этой площади.
Деформации тела бывают разные: растяжение, сжатие, сдвиг, кручение, изгиб. Мерой деформации является относительная деформация
.
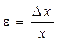Относительная деформация равна отношению абсолютной деформации Dx к первоначальному значению величины x, характеризующей размеры или форму тела.
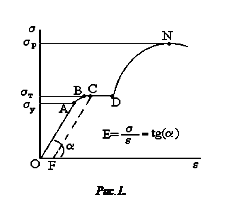Зависимость между напряжением s и относительной деформацией e показана на рис. 1, откуда видно, что линейная зависимость s(e) сохраняется лишь в небольшом интервале, до так называемого предела упругости (интервал О–А) sу. Предел упругости – максимальное напряжение, при котором еще возникают упругие деформации. За пределом упругости в теле возникают остаточные деформации (O–F) и график возвращения тела в первоначальное состояние после прекращения действия силы изобразится не кривой О–В, а параллельной ей С– F (параллельно из–за того, что tg угла наклона характеризуется модулем Юнга). В области В–С–D деформация возникает без увеличения напряжения, т.е. тело как бы течет. Это напряжение sт называют пределом текучести. Материалы, для которых область текучести значительна, называют вязкими, а если эта область отсутствует, то – хрупкими. Максимальное напряжение, возникающее в теле до разрушения, называют пределом прочности (sр).
Английский физик Р. Гук установил законы упругих деформаций. Основной закон (закон Гука): в пределах упругости напряжение, возникающее в теле, пропорционально его относительной деформации.
,
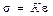где К – модуль упругости.
Закон Гука справедлив только на участке О–А.
При продольном сжатии или растяжении модуль упругости называется модулем Юнга, и закон Гука запишется так:
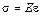, (1)
где E – модуль Юнга. Заменив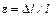 
и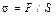 
, получим:
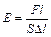. (2)
Если D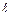 
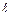= , то модуль Юнга E=s0=F / S, т.е. модуль Юнга равен нормальному напряжению, которое возникло бы в образце при увеличении его длины в два раза, если бы при этих деформациях выполнялся закон Гука. Единица измерения модуля Юнга [E]=[Н/м2].
Выражение (2) можно преобразовать
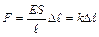или F = – kx, (3)
где k – коэффициент упругости, а Dℓ или x – удлинение стержня.
Выражение (3) также задает закон Гука : при упругих деформациях удлинение стержня пропорционально действующей на стержень силе.
Теория метода и описание установки
Определить модуль упругости можно методом изгиба стержня, обоими концами положенного на твердые опоры и нагруженного в середине грузом определенного веса. Действие этой силы вызовет деформацию изгиба.
В этом случае величина деформации характеризуется так называемой стрелой прогиба l (рис.2), т.е. тем расстоянием, на которое опускается точка приложения силы, действующей на стержень.
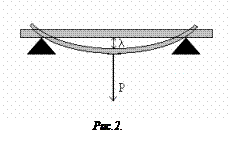Зная стрелу прогиба l, находят модуль Юнга по формуле:
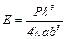, (4)
где P – сила, вызывающая деформацию (изгиб), ℓ – длина стержня, а – ширина поперечного сечения стержня, b – высота стержня.
Измерение и обработка результатов
1. Измеряют толщину, ширину пластины и расстояние между опорами несколько раз и определяют среднее значение.
Испытуемый стержень устанавливают между опорами и стременем для грузов, затем измеряют ненагруженное положение шкалы n0.
ℓ=, a = ,b = , n0 =
2. Стремя постепенно нагружают грузами (50, 100, 150, 200 г) и производят отсчет n ’1, n ’2, n ’3, n ’4.
3. Снимая грузы в обратном порядке, получим n ’’4, n ’’3, n ’’2, n ’’1.
4. Освободив стержень от дополнительных грузов, вновь определяют нулевое положение прибора.
5. Результаты занести в таблицу:
| № | Р, Н |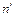 
| 
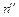
| l, м | E, Н/м2 |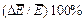 
|
| Cреднее значение | ||||||
Удобно при вычислении подсчитать величину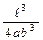 
= соnst, тогда формула (4) будет иметь вид 
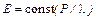. Массу грузов следует перевести в килограммы и вычислить вес по формуле Р = mg, где g = 9,81 м/с2.
Расчет погрешности
Относительная погрешность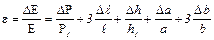 
Абсолютная ошибка ΔЕ равна: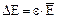 
; Δλ=0,01 мм; Δа=Δb=1 мм.
Задачи
1. Чему равна относительная деформация стального стержня, сжатого силой F= 3,14.106 Н, если диаметр стержня d=2 см, а его модуль Юнга Е=2.1011 Па?
Ответы:1) 1; 2) 0,3; 3) 0,77; 4) 0,005; 5) 0,002.
2. Латунная проволока диаметром d=0,8 мм имеет длину 3,6 м. Под действием силы F=25 Н проволока удлиняется на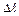 
=2 мм. Определите модуль Юнга для латуни.
Ответы:1) 1011 Па; 2) 9,8.1010 Па; 3) 9.1010 Па; 4) 3,8.1011 Па; 5) 2.1011 Па.
3. Чему равно удлинение латунного стержня длиной 4 м, имеющего площадь сечения 0,4 см2, под действием силы 1 кН?
Ответы:1) 8,3.10–3 м; 2) 4.10–3 м; 3) 2.10–3 м; 4) 10–4м; 5) 1,1.10–3м.
4. Под действием силы 100 Н проволока длиной 5 м и площадью поперечного сечения 2,5 мм2 удлинилась на 1 мм. Определите модуль Юнга.
Ответы:1) 2.1011 Па; 2) 1010 Па; 3) 27.109 Па; 4) 24.109 Па; 5) 3,8.1011 Па
5. При какой предельной нагрузке разорвался стальной трос диаметром 1 см, если предел прочности стали 1 ГПа?
Ответы:1) 50 кН; 2) 75 кН; 3) 93,7 кН; 4) 78,5 кН; 5) 130 кН.
6. К стальной проволоке длиной 1 м и радиусом 1 мм подвесили груз массой 100 кг. Чему равна работа растяжения груза?
Ответы:1) 1,2 Дж; 2) 0,323 Дж; 3) 0,176Дж; 4) 2,12 Дж; 5) 0,752 Дж.
Контрольные вопросы
1. Силы в механике.
2. Деформация. Виды деформации.
3. Объяснить график зависимости s от e.
4. Закон Гука.
5. Физический смысл модуля Юнга.
6. Рабочая формула. Теория метода.
Литература
1. Савельев И. В. Курс общей физики, т. 1. М.: Наука, 1989. с47–51.
2. Трофимова Т. И. Курс физики. М.: Высшая школа, 2002, с.43–45.
3. Детлаф А. А., Яворский Б. М. Курс физики, М.: Высшая школа, 1989, с.318–319.
Лабораторная работа 1.4