Измерение микрометром и обработка результатов измерений

Дата: 2025-04-30; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1. Измеряемый предмет (толстую проволоку или металлическую пластинку) помещают между упором Е и концом микрометрического винта А.

2. Находят значения k и n по шкале стебля D и барабана С. По формуле (6) проводят подсчет искомых величин.

3. Измерения диаметра проволоки L и толщины пластинки h повторяют не менее пяти раз в различных местах.

4. Вычислить абсолютную и относительную ошибки измерений. Результаты измерений и вычислений записать в таблицу:

№

Проволока

Пластина

k

n

L

DL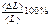

Lист

k

n

h

Dh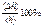

h ист

Среднее значение

Контрольные вопросы

1. Как измерить с помощью нониуса линейные размеры тела?

2. Что собой представляет линейный нониус?

3. Чему равна точность нониуса?

4. Что называется шагом микрометрического винта?

5. Как измерять микрометром размеры предмета?

Лабораторная работа 1.2

Определение момента инерции махового колеса и силы трения в опоре

Цель работы: определить момент инерции махового колеса и силы

трения в опоре.

Краткая теория

Закон сохранения энергии. В замкнутой системе энергия не исчезает и не возникает. Она только переходит из одной формы в другую.

Частным случаем этого закона является закон сохранения полной механической энергии. В замкнутой системе консервативных сил полная механическая энергия остается неизменной:

Е_кин+Е_пот = сonst,

где Е_кин= 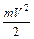– кинетическая энергия, которой обладает любое тело массы m, движущееся со скоростью V ;

Е_пот=mgh – потенциальная энергия тела, она определяется взаимным расположением тел h<<R_З.

Консервативными силами называются силы, работа которых не зависит от формы траектории, а зависит только от начального и конечного положения тела. Например, силы упругости, тяготения.

Диссипативными силами называют силы, работа которых зависит от длины и формы траектории. Например, силы трения.

Если в системе присутствуют диссипативные силы, то часть механической энергии переходит в тепловую.

Моментом инерции тела относительно данной оси вращения называется физическая величина, характеризующая меру инертности тела при изменении угловой скорости под действием вращающего момента. Момент инерции тела относительно данной оси вращения является величиной скалярной.

Моментом инерции материальной точки относительно произвольной оси называется произведение массы m этой точки на квадрат расстояния до оси:

J = mr ².

Момент инерции твердого тела относительно какой–либо оси равен сумме моментов инерции всех точек тела относительно этой оси:

.

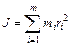Для сплошного тела момент инерции относительно какой–либо оси вычисляется:

,

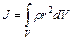где r – плотность, dV – элементарный объем.

Так как момент инерции зависит от оси вращения, то при определении момента инерции необходимо указывать ось вращения.

Вращающееся тело обладает кинетической энергией вращательного движения:

,

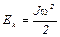где J – момент инерции тела, ω – его угловая скорость.

Теория метода и описание установки

Приборы и принадлежности: стойка, на которой закреплено маховое

колесо, линейка, секундомер, шнур с

грузом.

Целью работы является определение момента инерции махового колеса и силы трения в опоре.

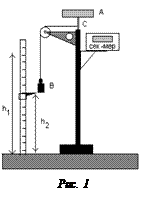Момент инерции махового колеса А и силу трения вала С в опоре можно определить при помощи прибора, изображенного на рис.1.

Маховое колесо приводится во вращательное движение грузом В. Груз В в начальный момент времени находится на высоте h_1, обладая потенциальной энергией mgh₁, где m – масса груза. Если предоставить возможность грузу падать с высоты h₁, то потенциальная энергия груза перейдет в кинетическую энергию поступательного движения груза E_k= 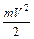, кинетическую энергию вращательного движения махового колеса 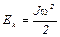и на работу по преодолению трения в опоре вала, A = f _тр h₁. По закону сохранения энергии:

mgh₁= 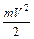+ + 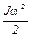f _тр h₁. (1)

Груз движется равноускоренно без начальной скорости. Скорость и ускорение соответственно выразятся:

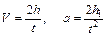. (2)

Угловая скорость махового колеса определится по формуле:

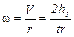, (3)

где r – радиус вала, на который наматывается шнур груза.

Сила трения f_тр вычисляется следующим образом. Маховое колесо, вращаясь по инерции, поднимает груз на высоту h₂<h₁ и потенциальная энергия груза на высоте h₂ будет равна mgh₂. Груз не поднимается на первоначальную высоту, так как часть энергии тратится на работу по преодолению силы трения в опоре:

mgh₁ – mgh₂=f _кр(h₁+h₂). (4)

Откуда сила трения равна:

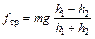. (5)

Подставив в (1) выражения для V , w, f _тр из (2,3,5) получим:

,

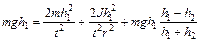преобразовав, получим:

.

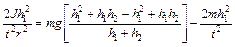Сделав соответствующие преобразования окончательно получим рабочую формулу :

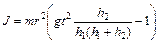. (6)

Измерение и обработка результатов

1. Наматывают на вал С шнур и поднимают груз на высоту h₁.

2. Поворачивают рычаг и отпускают груз, при этом включается секундомер – измеряют время падения груза с высоты h₁.

3. Определяют высоту h_2, на которую поднимется груз после опускания.

4. Измерив радиус вала r, вычисляют силу трения по формуле (5) и момент инерции махового колеса по формуле (6).

Полученные результаты заносят в таблицу

№ опыта	r, м	m, кг	h1, м	h2. м	t, c	fтр, Н	J		J ист
Среднее значение

Расчет погрешности

Абсолютная ошибка измерения момента инерции I:

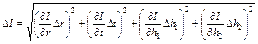
Частные производные находим по формулам:

,

,

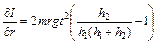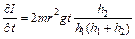
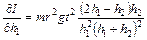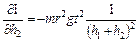
Δr = 0,1 мм; Δt = 0,1c; Δh₁ = Δh₂=0,5 см

Задачи

1. Диск радиусом 0,5 м вращается вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. Какая сила должна быть приложена к ободу диска, если через две минуты после начала движения диск делает 3 об/с? Масса диска 20 кг.

Ответы: 1) 1,5 Н; 2) 0,785 Н; 3)2Н; 4) 0,5Н; 5) 3,2 Н.

2. Диск весом 9800 Н и диаметром 80 см вращается с угловой скоростью 10 об/с. Какова кинетическая энергия диска?

Ответы:1) 10⁶Дж; 2) 3^.10⁵Дж; 3) 1,58^.10⁴Дж; 4) 0,5^.10³ Дж; 5) 7,5^.10² Дж.

3. Какова кинетическая энергия обруча, который катится без скольжения по горизонтальной плоскости со скоростью 10 м/с, если его масса равна 1 кг?

Ответы:1) 30 Дж; 2) 150 Дж; 3) 55 Дж; 4) 100 Дж; 5) 75 Дж.

4. Какую скорость приобретает сплошной цилиндр, скатившись без скольжения с наклонной плоскости высотой 1 м?

Ответы:1) 2,15 м/с; 2) 22 м/с; 3) 3,6 м/с; 4) 0,75 м/с; 5) 5,3 м/с.

5. Вычислить момент инерции однородного стального шара относительно оси, проходящей через его центр, если радиус шара равен 10 см. Плотность стали 7,8^.10³ кг/м³.

Ответы:1) 2,3 кг^. м²; 2) 13^. 10^–2 кг^.м²; 3) 3,32^.10^–2 кг^.м²; 4) 1,22^.10^–3 кг^.м²; 5) 0,77 кг^.м^2.

6. Диск диаметром 50 см и массой 5 кг вращается с угловой скоростью 100 рад/с. Определить тормозящий момент, если известно, что диск останавливается через две минуты после начала торможения.

Ответы:1) 0,013 Н^.м; 2) 0,23 Н^.м; 3) 1,2 Н^.м; 4) 0,018 Н^.м; 5) 0,31 Н^.м.