4. Потери по вызовам: , где µ — интенсивность потока.
(**)
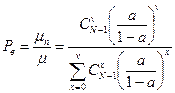Из соотношения формул (*) и (**) следует, что в полнодоступном пучке из v линий, на который поступает поток вызовов, и каждый источник создает одну и ту же нагрузку a, Pв при наличии N источников, численно равны Pt, при наличии (N-1) источника.
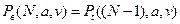, следовательно, 
,
.
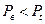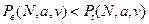Потери по вызовам табулированы. Чтобы по таблицам определить Pt, достаточно взять табличное значение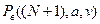 
.
5. Сравним системы M/M/V/K, где K=V и M/M/V/K/N, где K=V.
Первая формула Эрланга используется для расчета числа обслуживающих приборов в системах с потерями, при незначительном числе источников вызовов. Формула Энгсета более подходит при анализе систем с ограниченном числом источников вызовов. Выполним графическое исследование:
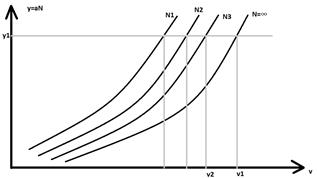
Из рисунка видно, что пропускная способность пучка y при заданных потерях возрастает с ростом емкости этого пучка. Она также возрастает и с ростом потерь (см. рассуждения для простейшего потока вызовов, для системы M/M/V/K, где K=V). Также на пропускную способность y влияет число источников вызовов N, причем, с уменьшением N, пропускная способность пучка растет. Следовательно, N1<N2<N3.
Рассмотрим следующий пример. Пусть необходимо определить ресурс системы, число линий v, если известно, что эта система должна обслуживать заданную нагрузку y1. Рассмотрим две кривые Nз и N= ∞. Возможны два варианта решения задачи:
а) применить наиболее распространенную модель обслуживания с N= ∞, тогда для обслуживания нагрузки требуется v1 линий;
б) выбрать формулу Энгсета, которая учитывает конечность числа источников Nз, и, в этом случае, нам достаточно иметь пучок из v2 линий. v2<v1, следовательно, пример показывает, что неточный выбор математической модели может привести к излишнему расходу ресурсов системы.
СИСТЕМЫ ТЕЛЕТРАФИКА БОЛЕЕ ОБЩЕГО ВИДА
Если система в своем описании выходит за рамки марковского процесса, тогда ее относят к системам телетрафика более общего вида.
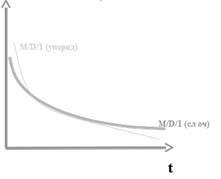
СИСТЕМА M/D/1 СО СЛУЧАЙНОЙ ОЧЕРЕДЬЮ
Обслуживание простейшего ПВ однолинейным пучком при постоянном времени обслуживания.
Исходные условия: λ k = const
Такая система исследована Берком. В силу сложности математического выражения для практического использования зависимости данной системы выражаются графически. Сравним их с результатом той же системы, но при обслуживании в порядке очереди.
