5. Исследуем первую формулу Эрланга, устремив v к бесконечности.
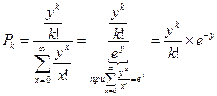
Таким образом, при v →∞, первая формула Эрланга переходит в формулу Пуассона. Здесь Pk — вероятность того, что в произвольный момент времени бесконечно-линейный пучок находится в состоянии k.
6. Рассмотрим графические зависимости:
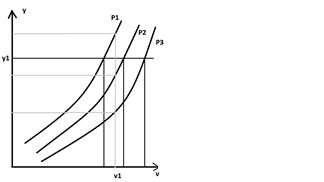
Пусть: P — потери; y — интенсивность поступающей нагрузки; v — емкость пучка; P=const.
Зафиксируем качество обслуживания P (P=const). Очевидно, что чем больше емкость пучка, тем большая нагрузка может быть обслужена этим пучком при заданных потерях. Зафиксируем некоторую нагрузку y1, проведем горизонтальную прямую и опустим перпендикуляры в точках пересечения с P. Чем больше потери, тем ниже качество обслуживания, следовательно, тем меньшим пучком линий может быть обслужена эта нагрузка. Можно сделать вывод, что p1>p2>p3.
Рассмотрим обратную зависимость. Зафиксируем значение v. Чем меньше потери, тем меньшая нагрузка может быть обслужена таким пучком линий.
Рассмотрим еще одну зависимость. Введем удельную нагрузку. Более наглядная взаимосвязь между нагрузкой, числом линий и качеством обслуживания наблюдается при рассмотрении графика зависимости удельной интенсивности нагрузки на линию c (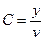 
). Рассмотрим c=f(v), при фиксированных потерях для разных значений этих потерь.
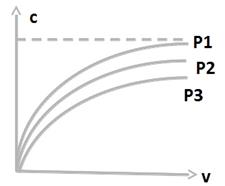
Из характера этих графиков видно, что в области малых пучков (обычно не больше 10-15 линий), существует низкое использование линий в пучке. Однако, с ростом v, происходит рост удельной пропускной способности. При больших значениях v (свыше 100 линий), наступает насыщение, то есть с увеличением v пропускная способность линии практически не меняется.
Рассмотрим график, показывающий различия между удельной нагрузкой на линии поступающей С и обслуженной Со в зоне насыщения.
c0=f(p)
c=f(p)
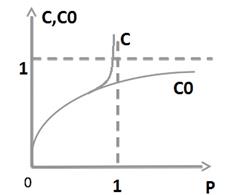
В области больших потерь, значения поступающей нагрузки не дает наглядной характеристики качества обслуживания (так как в области больших потерь, основная часть потока не обслуживается, а теряется). Из определения нагрузки, c0 (удельная нагрузка обслуживания на одну линию), не может быть больше 1, так как одна линия в единицу времени не может обслужить нагрузку более 1 Эрл.
7. Сопоставим две модели: M/M/V и M/M/V/K, где K=V (то есть вторая и первая формулы Эрланга).
Сравним вероятности Pi и потери по времени:
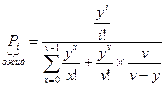— вторая формула Эрланга
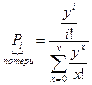— первая формула Эрланга
Сопоставление формул показывает, что вероятность Pi в системе с ожиданием будет меньше, чем Pi в системе с потерями. Pi (ожид)<Pi(пот).
Действительно, при сравнении формул видно, что знаменатель больше у yi в системе с ожиданием, следовательно, данная вероятность будет меньше. Этому есть и объяснение следующего рода: система с ожиданием примет бесконечно-большое число состояний, а система с потерями — только одно v+1 состояние. Так как сумма всех вероятностей равна единице для обеих моделей, то вероятность каждого состояния в системе с ожиданием будет меньше.
Сравним Pt в системе с ожиданием:
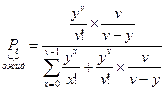
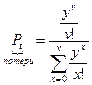
Без вывода принимаем, что Pt (ожид)>Pt(пот).
При заданной величине Pt, не только поступающая, но и обслуженная нагрузка в системах с потерями будет больше, чем в системах с ожиданием.
СИСТЕМА M/M/V/K/N, где K=V
Обслуживание примитивного потока вызовов полнодоступным пучком линий при показательном законе распределения длительности обслуживания без мест для ожидания и при ограниченном числе источников.
В данной модели принципиально новым является то, что входящий поток вызовов больше не является простейшим, а является потоком, который создается конечным числом источников. Для такого потока, параметр λk = α(N-k), где N-k — число свободных источников; α — коэффициент пропорциональности (численно равен параметру одного свободного источника).
Исходные условия:
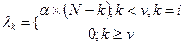
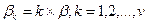
Условие устойчивости: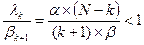 
. Следовательно, 
.
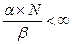Изобразим диаграмму состояний перехода:
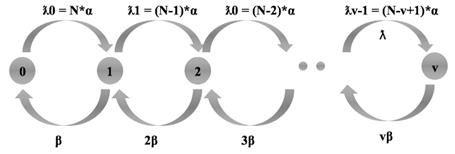
Определим Pk из основополагающего равенства теории телетрафика:
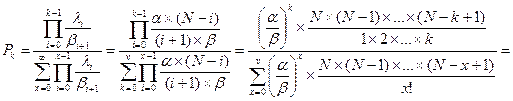
Воспользуемся выражением для определения числа сочетаний:
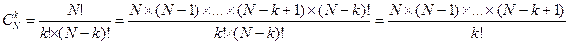
Следовательно,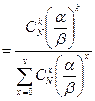 
.
Окончательно получаем, при k=i, k<v, следующее выражение:
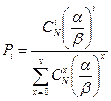— это формула Энгсета.
Распределение Энгсета представляет собой функцию от множества параметров: Pi=f (N,i, α , β , δ ). Данная формула является более общей, чем первая формула Эрланга. Если N устремить к бесконечности и одновременно параметр α устремить к нулю, так что произведение N α =const= λ, где λ — параметр потока вызовов всех свободных источников; в этих условиях, формула Энгсета переходит в первую формулу Эрланга.
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ M/M/V/K/N, где K=V
1. Рассмотрим взаимосвязь между параметром потока α (альфа) и нагрузкой, которая поступает от одного свободного источника, которую обозначим a (а). Для этого, рассмотрим систему без потерь, то есть такую, в которой число линий v равно числу источников v. В такой системе каждый источник может обслуживаться независимо от других источников. Для рассмотрения взаимосвязи между α и a, рассмотрим такой случай системы, когда v=N=1.
.
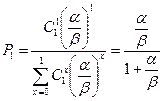Здесь, P1 — доля времени, в течение которого источник занят. Это численно соответствует нагрузке, поступающей от одного источника. Отсюда следует, что P1=a. Следовательно,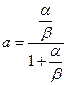 
. Следовательно, 
.
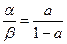Эта связь позволяет представить формулу Энгсета в другом виде: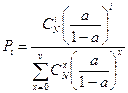 
.
2. Рассмотрим вероятности Pi в системе без потерь (если число источников совпадает с числом обслуживающих приборов). Для такой системы: =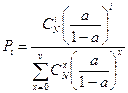
Домножим числитель и знаменатель на (1-a)N. Получим:
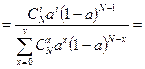
Рассмотрим знаменатель выражения:
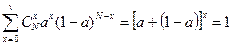(Сумма членов бинома Ньютона).
Следовательно: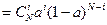 
.
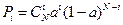— формула Бернулли.
Здесь, Pi — вероятность того, что в произвольный момент времени, из общего числа N источников, занято i источников.
3. 
. (*)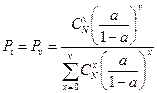