, следовательно, λ<β — условие устойчивости.
Обслуживание вызовов осуществляется в порядке поступления (FIFO).
Изобразим диаграмму для данной системы:
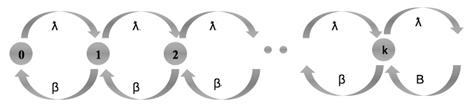
Определим характеристику Pk, воспользуемся основным равенством теории телетрафика:
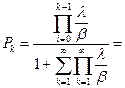
Рассмотрим отдельно сумму в знаменателе:
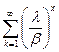 — это сумма членов бесконечного ряда, ряд сходится, так как λ<β
— это сумма членов бесконечного ряда, ряд сходится, так как λ<β
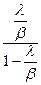
Тогда, 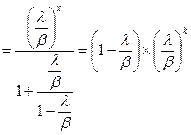
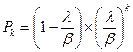 , где k=0,1,2,...
, где k=0,1,2,...
Известно, что интенсивность поступающей нагрузки: 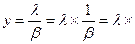 ŧ
ŧ 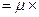 ŧ .
ŧ .
В рассматриваемом случае v=1 (то есть одна линия).
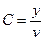 (удельная нагрузка на линию).
(удельная нагрузка на линию).
В данной модели, 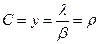 — коэффициент использования однолинейной системы.
— коэффициент использования однолинейной системы.
ρ≤1 — коэффициент использования в системе.
Следовательно, Pk= (1- ρ)Pk, где k=0,1,2,...
Так как, P0=1- ρ, следовательно, ρ =1- P0.
В устойчивых системах P0 >0, следовательно, 0 ≤ ρ < 1.
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ M/M/1
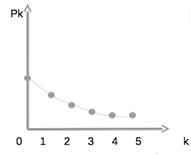
1. Рассмотрим графически функцию 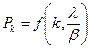 . Важно, что Pk зависит именно от соотношения
. Важно, что Pk зависит именно от соотношения 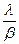 и не зависит отдельно от каждого из значений λ и β.
и не зависит отдельно от каждого из значений λ и β.
2. Среднее число вызовов в системе: ҟ 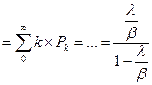 . Графически, это выражение выглядит следующим образом:
. Графически, это выражение выглядит следующим образом:
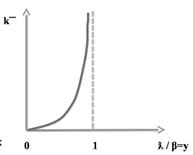
3. Аналогичный характер зависимости будет и для среднего времени пребывания в системе T; применим для получения T формулу Литтла: 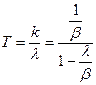 , при ҟ= λT.
, при ҟ= λT.
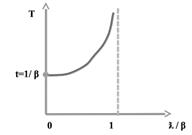
Если 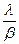 =0, то T=
=0, то T= 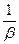 . Физический смысл этого состоит в том, что при
. Физический смысл этого состоит в том, что при 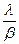 , вызовы не ожидают в очереди и длительность обслуживания вызова (ŧ) фактически совпадает со временем его пребывания в системе T. При
, вызовы не ожидают в очереди и длительность обслуживания вызова (ŧ) фактически совпадает со временем его пребывания в системе T. При 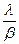 →1, возрастают ҟ и T. Такой вид зависимости характерен почти для всех систем телетрафика. Когда
→1, возрастают ҟ и T. Такой вид зависимости характерен почти для всех систем телетрафика. Когда 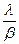 близко к единице, характеристики системы становятся неустойчивыми, они резко возрастают. Интуитивно объяснение этого явления состоит в том, что при случайном характере поступающего потока, возникают всплески нагрузки, которые перегружают систему, то есть за использование системы на грани ее пропускной способности, приходится дорого платить.
близко к единице, характеристики системы становятся неустойчивыми, они резко возрастают. Интуитивно объяснение этого явления состоит в том, что при случайном характере поступающего потока, возникают всплески нагрузки, которые перегружают систему, то есть за использование системы на грани ее пропускной способности, приходится дорого платить.
СИСТЕМА M/M/ ∞
Обслуживание простейшего потока вызовов бесконечно-линейным пучком при показательном законе распределения длительности обслуживания; без очереди. Данная модель называется моделью с немедленным обслуживанием. Действительно, в ней всегда найдется новый обслуживающий прибор, доступный поступившему вызову.
Определим исходные данные для такой системы:
λk=λ, где k=0,1,2,...
βk =k β, где k=1,2,...
Условия устойчивости: 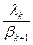 <1, следовательно,
<1, следовательно, 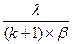 <1, следовательно,
<1, следовательно, 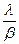 <∞
<∞
Диаграмма состояний перехода:
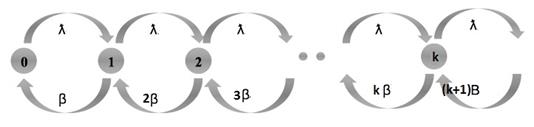
Рассчитаем из основополагающего равенства теории телетрафика
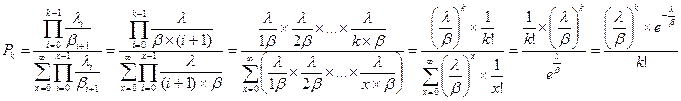 То есть,
То есть, 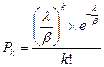 , где k=0,1,2,...
, где k=0,1,2,...
Мы получили формулу Пуассона, но здесь это распределение оценивает вероятность того, что бесконечно-линейный пучок в произвольный момент времени находится в состоянии с k занятыми линиями.
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ M/M/ ∞
1) Графическая зависимость рассматривалась в теме простейшего потока вызовов.
2) ҟ = 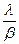 (берется без вывода).
(берется без вывода).
3) T= 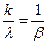 = ŧ.
= ŧ.
Действительно, время пребывания вызова в системе T будет равно среднему времени обслуживания ŧ, так как данная система является системой немедленного обслуживания.
Практическая значимость модели состоит в следующем: модель можно использовать для получения данных о нагрузке, которая поступает в систему. Действительно, вся поступающая нагрузка будет обслуженной, а, следовательно, может оцениваться через характеристики обслуженной нагрузки как среднее число вызовов, находящихся в системе в произвольный момент времени.
СИСТЕМА M/M/V
Обслуживание простейшего ПВ v-линейным полнодоступным пучком, при показательном законе распределения длительности обслуживания, с очередью и неограниченном числе мест для ожидания.
Практическим применением данной модели является расчет систем коммутации пакетов и сообщений. Также по системе с ожиданием работают многие службы сервиса в системах с коммутацией каналов.
Итак, имеется пучок линий, где v может меняться от одного до бесконечности. На систему поступает поток с параметром λ, а освобождение, связанное с обслуживанием вызовов, с интенсивностью β. Обслуживание вызовов осуществляется с ожиданием, причем вызовы обслуживаются в порядке их поступления. В системе может быть от 0 до v линий, причем при занятых v линиях на ожидании может быть 0,1,2,..., ∞ вызовов в очереди. Изобразим такую ситуацию на плоскости:
Вызов на обслуживании 0 1 2 … v
Вызов на ожидании 0
1
2
.
.
.
j
.
.
.
∞
Суммарное число состояний в такой системе будет бесконечным.
Рассмотрим условие устойчивости для такой системы:
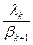 <1
<1
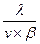 <1, следовательно,
<1, следовательно, 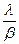 <v.
<v.
Исследуем данную систему при помощи процесса размножения и гибели, в котором будут следующие исходные условия: λk=λ; 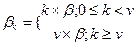 .
.
Обозначим, что для верхнего выражения βk =k β (i=k), а для βk =v β (j=k-v).

Ищем решение для Pk (вероятность того, что в системе находится k вызовов). Задачу поиска Pk разобьем на две части, так как зависимость βk также имеет две части. Вновь используем основополагающую формулу теории телетрафика: 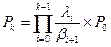 , где
, где 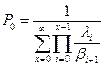 .
.
а) k ≤v, пусть k=i.
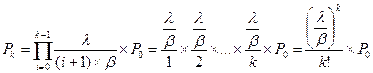
В рассмотренной модели M/M/1 соотношение 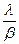 численно равно интенсивности поступающей нагрузки (y), следовательно, запишем
численно равно интенсивности поступающей нагрузки (y), следовательно, запишем 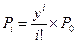 , где i ≤v.
, где i ≤v.
б) k ≥v, пусть j=k-v. Разобьем произведение на две части: 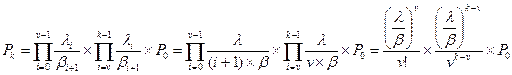
С учетом введенного индекса j, получим:
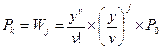 , при k-v=j.
, при k-v=j.
Wj — вероятность того, что в полнодоступном пучке из v-линий, все линии заняты и на ожидании находятся j-вызовов.
Определим вероятность P0. Будем исходить из нормировочного условия, согласно которому сумма состояний всех вероятностей состояний в системе равна единице,
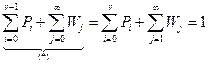
Воспользуемся нормировочным условием (*).
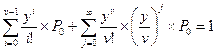 .
.
Следовательно, 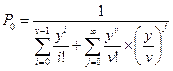 .
.
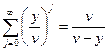 , следовательно,
, следовательно, 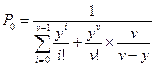 .
.
В окончательном виде, выражение для Pk принимает следующий вид:
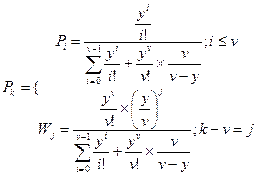
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ M/M/V
1) Вероятность потерь во времени P0 =P{ Ɣ >0}.
В системах с ожиданием, потери по времени численно равны вероятности ожидания. Другими словами, это вероятность того, что поступивший вызов не будет немедленно обслужен, а поступит на ожидание, и длительность этого ожидания Ɣ будет больше 0. Эти потери включают те состояния, когда занято v-линий и на ожидании находится j-вызовов (где j=0,1,2,...).
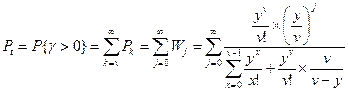
Рассмотрим числитель:
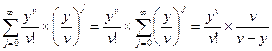 .
.
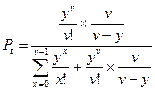 — это выражение называют 2-я (вторая) формула Эрланга.
— это выражение называют 2-я (вторая) формула Эрланга.
Таким образом, Pt — вероятность того, что поступающий вызов не застанет ни одной свободной линии.
Данная формула табулирована (то есть, есть таблицы).
2) Функция распределения времени ожидания начала обслуживания.
Потери по времени не указывают на характер распределения времени ожидания начала обслуживания, поэтому более общей является характеристика P{ Ɣ >t} — это вероятность того, что вызов, поступающий в произвольный момент времени, попадает на ожидание, и время ожидания будет больше, чем t. При этом обычно, и Ɣ и t, определятся в относительных единицах, а именно — единицах длительности обслуживания.
Для оценки P{ Ɣ >t} можно воспользоваться формулой полной вероятности (ФПВ). Итоговое выражение берем без вывода:
P{ Ɣ >t}=P{ Ɣ >0}e- β(v-y)t . (*)
Данное выражение (*) также табулировано. Выражение (*) справедливо по отношению к любому поступившему вызову, в том числе и такому, которому не придется ждать.
Рассмотрим аналогичную вероятность для вызова, про который известно, что он точно попадает в ожидание. Обозначим эту вероятность Pз.
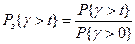 .
.
В итоге получим:
Pз { Ɣ >t}=e- β(v-y)t . (**)
Рассмотрим графическую интерпретацию формул (*) и (**). Изобразим графики сначала в общем виде. За счет экспоненты, они имеют убывающий характер. Пусть v=const. Введем величину 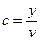 (нагрузка на одну линию) и рассмотрим характер этих зависимостей.
(нагрузка на одну линию) и рассмотрим характер этих зависимостей.
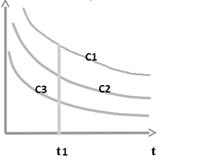
Возьмем некоторую точку t1 и поднимем перпендикуляр до пересечения с этими кривыми. Обозначим c1, c2 и c3. Выше располагается кривая, которая имеет большие потери: c1>c2>c3. Чем больше c, тем выше доля вызовов, время ожидания начала обслуживания у которых превысит t1.
Изобразим на другом графике:
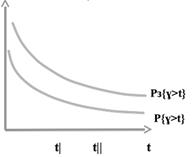
При фиксированных значениях v и c, с увеличением t, вероятность того, что длительность ожидания начала обслуживания Ɣ превысит заданную величину t, уменьшается, а кривая подмножества задержанных вызовов располагается выше.
3) ɣ ‒ — среднее время ожидания начала обслуживания и ɣ ‒ з — среднее время ожидания начала обслуживания для задержанных вызовов.
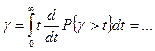 — без вывода, через математическое ожидание ɣ ‒ получаем:
— без вывода, через математическое ожидание ɣ ‒ получаем:
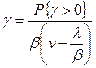 ,
,
где 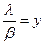 — интенсивность обслуженной нагрузки.
— интенсивность обслуженной нагрузки.
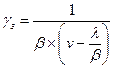
4) Среднее число вызовов, находящихся на ожидании ɉ. Здесь речь идет о функции распределения дискретной случайной величины числа вызовов. Поэтому при оценке выражения используется не интеграл, а сумма:
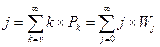 ,
,
Где j — число вызовов, находящихся на ожидании; Wj — вероятность того, что в системе есть j вызовов, находящихся на ожидании.
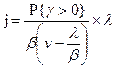 — то же самое выражение можно получить из формулы Литтла.
— то же самое выражение можно получить из формулы Литтла.
j= ɣ ‒ λ — частный случай формулы Литтла для очереди.
СИСТЕМА M/M/V/K, где K=V
Обслуживание простейшего ПВ, v-линейным пучком, при показательном законе распределения длительности обслуживания, без мест для ожидания. Система, которая будет иметь явные потери.
Данная система является системой с потерями, так как вызов, поступивший в момент занятости всех линий в пучке, отвергается системой. Следовательно, такая система может находиться в состояниях с 0 вызовов, 1 вызовом, … , v вызовами (суммарное число состояний конечно и равно (v+1)).
Исходные условия. Простейший поток, следовательно: 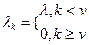 .
.
Параметр освобождения: 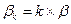 , при
, при 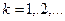 (так как
(так как 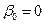 ).
).
Условие устойчивости: 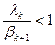 , следовательно,
, следовательно, 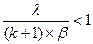 , при
, при 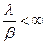 .
.
Диаграмма состояний перехода для системы M/M/V/K, где K=V:
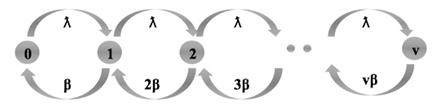
Оценим 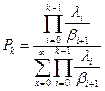 . Подставим в это выражение исходные условия:
. Подставим в это выражение исходные условия:
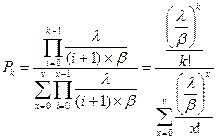 , при
, при 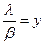 . Следовательно:
. Следовательно:
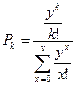 — это формула носит название 1-ой (первой) формулы Эрланга,
— это формула носит название 1-ой (первой) формулы Эрланга,
где: Pk — вероятность того, что в полнодоступном пучке из v-линий занято точно k линий, если на этот пучок поступает простейший поток вызовов; при этом длительность обслуживания подчиняется показательному закону, а дисциплина обслуживания в такой системе - с потерями.
ОСНОВНЫЕ ХАРАКТЕРИСИКИ СИСТЕМЫ M/M/V/K, где K=V
1. Исследуем Pk графически.
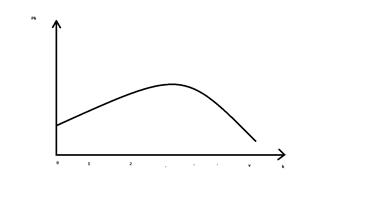
Таким образом, Pk — это функция распределения дискретной случайной величины k случайных вызовов. Огибающие этой функции близки к огибающим распределения Пуассона.
2. Pt — потери по времени (доля времени, в течение которого вызов, если он поступит, будет потерян). Это время образуется, когда заняты все линии. Для этого приравняем Pt к Pv, следовательно, 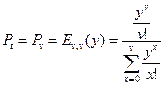 , где y — интенсивность поступающей нагрузки.
, где y — интенсивность поступающей нагрузки.
Потери по времени табулированы в таблицах Пальма и Башарина.
3. Pв — потери по вызовам, которые могут быть оценены через соотношение интенсивности потерянного и поступающего потоков вызовов (так как речь идет о простейшем потоке вызовов, который обладает свойством стационарности).
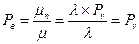 . Следовательно, потери по вызовам численно равны потерям по времени.
. Следовательно, потери по вызовам численно равны потерям по времени.
Можно доказать, что и другие виды потерь, такие как потери по нагрузке (Pн), также равны Pv: 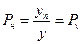
Следовательно, 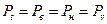 .
.
4. Рекуррентные соотношения первой формулы Эрланга. Рассмотрим некоторые значения Pi и Pi-1, где 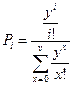 , а
, а 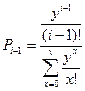 .
.
Если 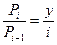 , следовательно, можем считать (i-1), через i и наоборот. То есть,
, следовательно, можем считать (i-1), через i и наоборот. То есть, 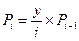 и
и 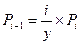 .
.








