2. Работа, исполненная системой (обслуженная нагрузка).
3. Работа, незавершенная системой (избыточная, или остаточная нагрузка).
Так как каждый вызов вносит в систему работу, измеряемую временем, определим разные виды работ математически.
1) Поступающая нагрузка.
Рассмотрим математическое ожидание работы, вносимой в систему за промежуток времени [t1;t2).
МА(t1;t2)= µ(t2-t1)ŧ,
где М — математическое ожидание, А — поступающая нагрузка, µ — интенсивность нагрузки, ŧ — среднее время обслуживания. (t2-t1) — длительность интервала.
Таким образом, поступающая нагрузка оценивается не только через количество вызовов µ(t2-t1), которые поступили на промежутке вызовов (t1;t2), но зависит и от длительности обслуживания вызовов ŧ.
2) Обслуженная нагрузка.
Для обслуженной нагрузки математическое ожидание значения нагрузки
МУ(t1;t2)= ӿ(t2-t1),
где ӿ — среднее число вызовов; (t2-t1) — длина рассматриваемого промежутка вызовов.
3) Избыточная или остаточная нагрузка.
Следовательно, незавершенная системой нагрузка
U(t1;t2)=A(t1;t2)-Y(t1;t2),
где А — поступившая нагрузка; Y — обслуженная нагрузка.
Нагрузка измеряется в часозанятиях. Эта единица характерна для европейских стран, в том числе и для России, а в Америке используется секундозанятие. Обычно рассматривают нагрузку в единицу времени, придавая ей значение интенсивности нагрузки. Следовательно, интенсивность любого вида нагрузки можно записать следующим образом:
1) y= µŧ, где y — интенсивность поступающей нагрузки;
2) y0= ӿ, где y0 — обслуженная нагрузка;
3) u=y-y0.
Единица измерения интенсивности нагрузки - часозанятие, разделенное на час, для неё вводится название Эрл (произносится «Эрланг»).
На практике, часто удобно оценивать интенсивность поступающей нагрузки по следующей формуле: y=N ĉŧ, где N — источник вызовов; ĉ — среднее число вызовов от одного источника; ŧ — среднее время обслуживания одного вызова.
ХАРАКТЕРИСТИКИ КАЧЕСТВА ОБСЛУЖИВАНИЯ
Характеристики качества обслуживания и эффективности систем распределения информации различаются в зависимости от конкретных задач по расчетам таких систем, от структуры самой системы, от дисциплины обслуживания и других факторов.
Рассмотрим важнейшие из этих характеристик:
1. Вероятность потерь.
В зависимости от дисциплины обслуживания различаются явные (когда вызов получает отказ в обслуживании) и условные (или неявные) (когда вызов должен ожидать обслуживания) потери. Рассмотрим виды потерь в системах с повторными вызовами, с потерями и с ожиданиями.
1) В системах с повторными вызовами различают следующие виды потерь:
а) потери по времени Pt — вероятность потери первичного вызова, или доля времени, в течение которого заняты все ресурсы системы, способные обслужить вызов, если он поступит. Иногда говорят, что это опасное время, в течение которого вызовы теряются.
б) потери по вызовам Pв — вероятность безуспешного вызова, оцениваемая как отношение всех потерянных вызовов (как первичных, так и повторных) ко всем поступившим вызовам: 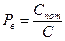 . Для стационарных потоков Pв можно рассматривать как отношение интенсивностей потерянных потоков к поступающим
. Для стационарных потоков Pв можно рассматривать как отношение интенсивностей потерянных потоков к поступающим 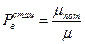 .
.
в) потери сообщения Pc — учитывает функцию настойчивости α, которая расценивается, как вероятность того, что абонент после очередного неуспешного вызова, через случайное время создаст следующий повторный вызов. Статистика показывает, что величина α составляет, приблизительно 0,8-0.9. Потеря сообщений является наиболее объективной характеристикой в системе с повторными вызовами.
Pc=LPв (1- α ), где L — число вызовов, которые необходимо послать, чтобы появился успешный вызов. Математическое ожидание геометрического распределения, оценивает 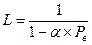 . Очевидно, что величина (L-1) - это среднее число неуспешных вызовов, после которого появится успешный вызов. Следовательно,
. Очевидно, что величина (L-1) - это среднее число неуспешных вызовов, после которого появится успешный вызов. Следовательно, 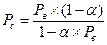 .
.
Существуют и другие виды потерь, например, потери по нагрузке (Pн), потери по линиям (Pv), и так далее. Независимо от вида потерь, любые потери, как вероятностный показатель, принимают значения в диапазоне от 0 до 1 и измеряются в процентах (%), или промиллях (‰).
Рассмотрим пример. Пусть поступило 1000 вызовов, 5 из которых были потеряны. Тогда можно определить Pв как: 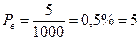 ‰.
‰.
2) В системах с потерями рассматриваются такие же характеристики качества, так как ранее было показано, что система с потерями — это частный случай системы с повторными вызовами. Оценим величину потерь сообщений в системе с потерями. Для таких систем, функция настойчивости α =0, следовательно, Pc=Pв.
3) В системах с ожиданием широко распространена такая характеристика качества, как вероятность ожидания P{ Ɣ >0}. Это вероятность того, что поступающий вызов должен ждать, или, иначе говоря, вероятность задержки вызова, или вероятность того, что длительность ожидания начала обслуживания Ɣ будет больше нуля. Однако данная характеристика дает неполную картину качества обслуживания, так как не позволяет судить о законе распределения Ɣ. По этой причине, более общей характеристикой является P{ Ɣ >t} — это вероятность того, что Ɣ будет больше некоторой, заранее заданной, величины t. Обычно и Ɣ и t измеряются в относительных единицах времени, а именно, в единицах длительности обслуживания.
При учете характеристик качества, в системе с ожиданиями также используются средние величины. К их числу относятся: среднее время ожидания начала обслуживания ɣ ‒ и среднее число вызовов, находящихся на ожидании ɉ. Для ɣ ‒ обычно рассматриваются две величины: ɣ ‒ и ɣ ‒ з — среднее время ожидания, относящиеся только к тем вызовам, которые фактически ожидают. В общем случае, ɣ ‒ будет меньше, или равно, чем ɣ ‒ в ( ɣ ‒ ≤ ɣ ‒ в ).
2. Пропускная способность.
Пропускная способность системы — это свойство системы, заключающееся в ее возможности выполнять работу по доставке информации. Пропускная способность характеризуется объемом работы, производимым в единицу времени в соответствии с техническими характеристиками системы и режимом функционирования. Пропускную способность принято рассматривать с вероятностной и технической сторон. Вероятностная оценка связана с проблемой доставки информации в условиях обслуживания случайных потоков вызовов. Техническая сторона связана с техническими характеристиками оборудования системы. Каждая из сторон характеризуется своими показателями. Основными для вероятностной стороны является показатель пропускной способности, а для технического аспекта — показатель производительности системы.
Пропускная способность С эквивалентна средней мощности, развиваемой системой при заданном качестве, то есть это интенсивность обслуживания нагрузки (y0) при заданном качестве: C=y0. Техническая сторона характеризуется производительностью П и эквивалентна максимальной интенсивности нагрузки: П=y0max. Таким образом, П характеризует технические возможности оборудования при непрерывной нагрузке системы без интервалов простоя. В качестве показателя пропускной способности нередко рассматривается и интенсивность поступающей нагрузки при заданном качестве. Это объяснимо по двум причинам:
1) поступающая нагрузка находится в явной зависимости от вероятности потерь. Для обслуженной нагрузки явной зависимости обычно нет, поэтому работать с поступающей нагрузкой математически удобнее.
2) так как системы распределения информации работают обычно с высоким качеством обслуживания, что соответствует малому значению вероятности потерь, следовательно, различия между поступающей y и обслуженной y0 нагрузками будет незначительны, и в инженерных расчетах ими можно пренебречь: y ≈ y0.
Итак, пропускная способность y является сложной функцией от многих параметров (A(x) — закон, по которому в систему поступают вызовы; S — структура системы; ДО — дисциплина обслуживания; B(x) — функция распределения длительности обслуживания; P — потери): y=f(A(x),S,ДО,B(x),P). Часто указанная зависимость рассматривается относительно величины потерь: p=g (y,A(x),S,ДО,B(x),P).
3. Время доставки сообщений.
В настоящее время все большую значимость приобретает такая характеристика качества обслуживания, как время доставки сообщений. Данное время — это сумма времен ожидания, обработки и передачи сообщения, начиная с момента поступления этого сообщения в систему и заканчивая моментом его выхода из системы. Различают среднее, наибольшее и наименьшее время доставки. Среднее время доставки принято интерпретировать, как среднее время пребывания в системе T. Оно определяется следующим соотношением: T= ɣ ‒ + ŧ, где ɣ ‒ — среднее время ожидания начала обслуживания. Наряду с T интерес представляет такая характеристика, как среднее число требований в системе ҟ. Эти величины (T и ҟ) связаны между собой формулой Литтла:
ҟ=λT,
где λ — параметр потока вызовов (для стационарного потока равный интенсивности поступлений вызовов в систему).
Математическое доказательство формулы Литтла сложное, поэтому воспользуемся распространенным интуитивным пояснением. Оно сводится к утверждению, что требования, входящие в систему, находят в ней то же самое число требований ҟ, которое будет в системе, когда данный вызов покидает систему. Формула Литтла не зависит ни от каких частных ограничений (ни на характер поступающего потока, ни на функцию длительности обслуживания, ни на дисциплину обслуживания, ни на саму систему, и так далее). Эта формула может рассматриваться по отношению к отдельным частям системы обслуживания:
ҟs=λɣ ‒; ҟv=λŧ,
где ҟs — средняя длина очереди, а ҟv — среднее число вызовов в обслуживающих приборах.
Часть 3
КЛАССИЧЕСКИЕ СООТНОШЕНИЯ
И ВАЖНЕЙШИЕ ВЕРОЯТНОСТНЫЕ ПРОЦЕССЫ
К важнейшим вероятностным процессам в теории телетрафика относятся, так называемые марковские процессы. В этих процессах устанавливается очень простая форма взаимосвязи между случайными величинами, которые образуют этот процесс: если известно состояние процесса в момент времени t, то изменение состояния этого процесса после момента времени t, в вероятностном смысле не зависит от течения этого процесса до данного момента времени t. Другими словами, для марковского процесса будущее определяется известным настоящим и не зависит от прошлого.
Различают дискретные и непрерывные марковские процессы. Для дискретного марковского процесса переходы из одного состояния в другое осуществляются в дискретные моменты времени, а для непрерывного — в любые моменты времени.
Марковские процессы бывают однородными и неоднородными. Для однородных процессов вероятности перехода из одного состояния в другое не зависят от времени. Соответственно, неоднородные процессы зависят от времени. Мы будем изучать однородные непрерывные марковские процессы.
Рассмотрим модель марковского процесса в виде коммутационной системы, в которой число обслуживаемых источников нагрузки может как совпадать, так и не совпадать с числом занятых линий в этой системе. Несовпадение характеризует достаточно редкие случаи работы коммутационных систем, однако, в рамках классических, или элементарных систем теории телетрафика, рассматривается частный случай, когда число занятых источников нагрузки всегда совпадает с числом линий в этой системе. Этому условию соответствует полнодоступный пучок линий (любому вызову доступна любая свободная линия в этом пучке). Полнодоступный пучок может принимать различное число состояний, в зависимости от дисциплины обслуживания. В системах с потерями, число состояний может быть 0,1,2,...v (где v — число линий полнодоступного пучка), всего — (v+1) состояние. Если все линии пучка заняты, система не принимает на обслуживание новые вызовы. В системах с ожиданием при наличии v занятых линий, вызовы не отвергаются системой, а ставятся на ожидание. При этом при v занятых линиях, в очереди могут находиться 0,1,2,... вызовов. Следовательно, суммарное число состояний в этой системе бесконечно. Итак, классические системы с чистым ожиданием имеют бесконечное число состояний.
Сформулируем задачу обслуживания вызовов полнодоступным пучком с общих позиций. Пусть v(t) — число линий в полнодоступном пучке в момент времени t. И пусть в этот момент занятыми окажутся k линий (k=0,1,2,...). Следовательно, такую систему можно рассматривать как систему, в которой существует бесконечно большое число состояний, и в этой системе может быть занято любое число линий. Такую ситуацию можно рассматривать как бесконечно-линейный пучок (v= ∞). Введем следующее обозначение: если в бесконечно-линейном пучке занято k линий, то будем считать, что он находится в состоянии k. Проследим за состоянием этого пучка на некотором промежутке времени: [0;t+ τ ). Пусть в момент времени t=0 система находится в состоянии j, и к моменту времени t+ τ, перешла в состояние k. Следовательно, в некоторый промежуточный момент времени t, система перешла через некоторое промежуточное состояние r (0 ≤ r ≤ v), а за промежуток времени от t до t+ τ, перешла в состояние k. Оценим вероятность перехода системы из состояния j в состояние k, для чего воспользуемся ФПВ для независимых событий. Согласно этой формуле, 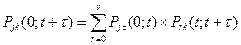 . (*)
. (*)
В теории случайных процессов, данное выражение называется уравнением Колмогорова-Чэпмена. Оно справедливо не только для непрерывных однородных марковских процессов, но и для дискретных неоднородных. Это уравнение справедливо, при следующих условиях: 0 ≤ j ≤ v; 0 ≤ k ≤ v; 0 ≤ r ≤ v.
Важнейшим случаем марковского процесса является процесс размножения (поступление вызовов в систему) и гибели (уход вызовов из системы). Процесс размножения и гибели — это марковский процесс с непрерывным параметром t, имеющий конечное (0,1,2,...,v) или счетное количество состояний, в котором за промежуток времени [t;t+ τ), при τ → 0, с вероятностью более 0 (то есть с конечной вероятностью) возможен непосредственный переход системы только в соседнее состояние (то есть (k-1), k, (k+1)). Во все другие состояния система переходит с вероятностью o( τ ). Ранее рассмотренный пуассоновский процесс — это частный случай процесса размножения и гибели, в котором гибели вызовов не происходит (его называют процессом чистого размножения).
ПРОЦЕСС ОБСЛУЖИВАНИЯ СИММЕТРИЧНОГО ПОТОКА ПОЛНОДОСТУПНЫМ ПУЧКОМ (ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПРОЦЕССА РАЗМНОЖЕНИЯ И ГИБЕЛИ)
Постановка задачи. Рассмотрим полнодоступный пучок из бесконечно большого числа линий (v= ∞). Пусть на этот пучок поступает симметричный поток вызовов с параметром λk. λk — параметр поступления вызовов потока в состоянии k (в большинстве случаев можно считать, что это интенсивность размножения в состоянии k). Интенсивность обслуживания вызовов характеризуется параметром ßk, что можно считать интенсивностью (скоростью) гибели в состоянии k. λk и ßk не зависят от времени, а зависят только от состояния k. Следовательно, в силу свойств марковских процессов, события размножения и гибели являются независимыми. Рассмотрим динамику процесса, описываемым уравнением (*). Определим вероятность Pk (t), где Pk (t) — вероятность того, что в полнодоступном пучке на момент времени t занято k линий. Общий подход к решению данной задачи рассмотрим с учетом того, что возможны переходы только в соседние состояния. Покажем все возможные события, которые приводят к тому, что в момент времени t+ τ, в системе будет точно k вызовов, в виде следующей таблицы:
| t+τ | t | τ | |
| k | k-1 | 1 вызов | Pk-1(t) Pk-1,k(τ)=Pв(τ) Pk (t+τ)=Pk-1(t)Pв(τ) |
| k+1 | 1 освобождение | Pk+1(t) Pk+1,k(τ)=Pосв(τ) Pk (t+τ)=Pk+1(t)Pосв(τ) | |
| k | 0 вызовов 0 освобождений | Pk (t) Pk,k (τ)=[1-Pв(τ)-Pосв(τ)] Pk (t+τ)=Pk(t)[1-Pв(τ)-Pосв(τ)] | |
| k=-2,-3,... k=2,3,... | 2 вызова, 3 вызова, … 2 осв., 3 осв., ... | o(τ) — указывает, что в процессе размножения и гибели, кратные рождения и кратные гибели запрещены |
По формуле полной вероятности (ФПВ) получаем:
Pk (t+τ)=Pk-1(t)Pв(τ)+Pk+1(t)Pосв(τ)+Pk(t)[1-Pв(τ)-Pосв(τ)] — это выражение справедливо для случаев k ≥ 1.
P0(t+τ)=P1(t)Pосв(τ)+P0(t)[1-Pосв(τ)-Pв(τ)] — для k=0.
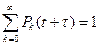
Необходимо решить данную систему из бесконечно большого числа уравнений для Pk (t). Определим вероятность поступления вызова на отрезке τ и вероятность освобождения вызова на τ. Для определения Pв (τ), воспользуемся определением параметра потока с простым последействием: 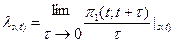 , при условии, что система в момент времени t находится в состоянии S(t); этой записи эквивалентна следующая: π1(t;t+τ)=λ S(t) τ+o(τ), при τ → 0.
, при условии, что система в момент времени t находится в состоянии S(t); этой записи эквивалентна следующая: π1(t;t+τ)=λ S(t) τ+o(τ), при τ → 0.
Нами рассматривается симметричный ПВ, в котором λS(t) = λk. Следовательно, π1(t;t+τ)=λkτ+o(τ), при τ →0. Так как симметричный поток является ординарным потоком, а для ординарного потока, вероятность π2(t;t+τ)=o(τ), при τ →0. Pв ( τ)=λkτ+o(τ), при τ→0.
Рассуждая аналогичным образом, для Pосв ( τ)=βkτ+o(τ), при τ→0. Подставим значения Pв (τ) и Pосв (τ) в полученную систему:
Pk(t+τ)=Pk-1(t)[ λkτ+o(τ)]+Pk+1(t)[βkτ+o(τ)]+Pk(t)[1-(βkτ+o(τ))-(λkτ+o(τ))]
P0(t+τ)=P1(t)[β1τ+o(τ)]+P0(t)[1-(βkτ+o(τ)-(λkτ+o(τ))]
Перенесем в левую часть вероятность Pk (t), и поделим обе части на τ:
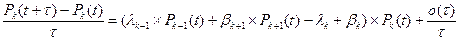 , где k ≥ 1.
, где k ≥ 1.
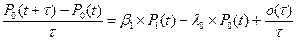 , где k =0.
, где k =0.
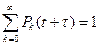
Перейдем к пределу, при этом, в левой части получим 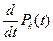 и
и 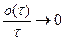 :
:
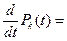 λk-1Pk-1(t)+βk+1Pk+1(t)-λk+βk Pk(t)
λk-1Pk-1(t)+βk+1Pk+1(t)-λk+βk Pk(t)
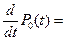 β1 P 1 ( t )-λ0 P 0 ( t ) (**)
β1 P 1 ( t )-λ0 P 0 ( t ) (**)
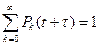
Система (**) - это система дифференциально-разностных уравнений, решением которых является характеристика Pk (t). Эта характеристика является основной для решения многих задач ТТ.
ОБЩЕЕ РЕШЕНИЕ ДЛЯ СТАЦИОНАРНОГО РЕЖИМА
Будем рассматривать полнодоступный пучок в состоянии статистического равновесия. Перейдем от вероятности Pk (t) к аналогичной вероятности для стационарного режима. Для этого определим, устанавливается ли вероятность Pk (t) независимо от времени.
Введем следующее предположение: 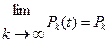 . Для симметричного потока известно, что при t →∞, он стремится к стационарному потоку. Тогда Pk — это вероятность того, что в произвольный момент достаточно отдаленного будущего будет равно k вызовов.
. Для симметричного потока известно, что при t →∞, он стремится к стационарному потоку. Тогда Pk — это вероятность того, что в произвольный момент достаточно отдаленного будущего будет равно k вызовов.
Преобразуем (**) в соответствии с принятым предположением. Очевидно, что для стационарного режима: 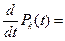
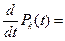 0. Тогда:
0. Тогда:
0= λk-1Pk-1+βk+1Pk+1-(λk+βk )Pk,при k ≥1.
0= β1P1-λ0Pk, при k=0. (***)
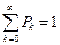
Эти уравнения известны, как уравнения движения Колмогорова для стационарного режима (уравнения статистического равновесия).
Решим систему (***) методом последовательной подстановки:
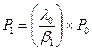
k=1, 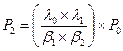
Можно убедиться в том, что общее решение можно искать в виде: 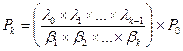
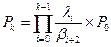 , при k =0,1,...
, при k =0,1,...
Это предположение можно проверить методом математической индукции, подставляя Pk в выражение для Pk+1, для k=0, получаем: 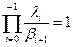 . Справедливость этого была доказана в теории множеств.
. Справедливость этого была доказана в теории множеств.
Найдем Pi, воспользовавшись нормирующим уравнением:
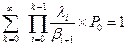 ;
;
следовательно, 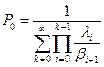 .
.
В окончательном виде получим основополагающее равенство классической (элементарной) теории телетрафика, которое является исходной моделью для анализа всех схем.
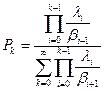 , при k =0,1,2,...
, при k =0,1,2,...
Рассмотрим условие устойчивости для этой формулы: 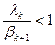 , так как требуется, чтобы P0 было больше 1; данное утверждение может быть доказано математически.
, так как требуется, чтобы P0 было больше 1; данное утверждение может быть доказано математически.
Физическая интерпретация этого условия позволяет получить частные математические соотношения, которые характеризуют модели обслуживания ПВ, укладывающиеся в рамки марковских процессов. Эти частные модели могут иметь различные характеристики поступающего потока (простой или примитивный). Но при этом всегда функция распределения промежутков между вызовами A(x) должна подчиняться показательному закону.
Это могут быть модели с потерями, или с ожиданием, но длительность обслуживания B(x) также должна всегда подчиняться показательному закону.
В 1910 году Эрлангом была выдвинута идея статического равновесия, которая позволила иным путем подойти к схеме (***). Им было предложено описывать движение процесса (размножения и гибели) при помощи диаграмм состояний и переходов. Состояния k на диаграмме обозначались овалом (кругом) (k – число вызовов в системе). Овалы соединялись ребрами со стрелками. Ребра указывают возможные переходы из одного состояния в другие. Ребрам приписываются числа, характеризующие интенсивности размножения и гибели.
Эрланг предполагал, что стационарное состояние процесса должно удовлетворять, так называемому, условию сохранения.
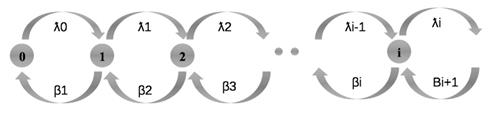
Для каждого состояния схемы, входящий поток события должен быть равен исходящему. Для состояния (i), входящий поток образуется индексами λi-1 и βi-1, исходящий поток образуется дугами с индексами λi и βi. Тогда интенсивность потока в состоянии i: λk-1Pk-1+βk+1Pk+1
λkPk+βkPk =( λk+βk ) Pk
В условиях статистического равновесия интенсивности равны:
λk-1Pk-1+βk+1Pk+1 =( λk+βk ) Pk
ЭЛЕМЕНТАРНЫЕ СИСТЕМЫ ТЕОРИИ ТЕЛЕТРАФИКА
СИСТЕМА M/M/1
Обслуживание простейшего потока вызовов однолинейным пучком при показательном законе распределения длительности обслуживания и бесконечно-большом числе мест для ожидания.
Данная модель используется для расчета характеристик процессорных устройств в управлении, а также при расчете характеристик коммутирующих каналов.
Исходные условия:
λk = λ=const, при k=0,1,2,...
β k = β =const, при k=1,2,... (β 0 =0)
A(x)=1-e- λ x
B(x)=1-e- β x








