2. Оценим сумму вероятностей событий простейшего потока . Следовательно, .

Дата: 2025-04-30; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

3. Исследуем функцию Пуассона графически. Функция Пуассона является функцией дискретной случайной величины числа вызовов. Рассмотрим характер изменения данной функции при изменении параметра λ.

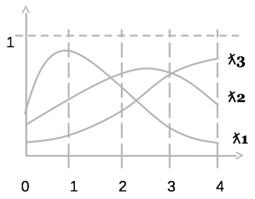
Pk (f)=f(k)

Пусть t=1

λ - vor

 

Будем для простоты рассматривать огибающие вероятностей дискретной случайной величины. С ростом λ огибающая значений вероятностей перемещается вправо и принимает вид все более симметричной относительно оси координат. Следовательно, λ1<λ2<λ3. На практике при λt>10 имеет место хорошее совпадение между огибающей закона Пуассона и нормальным законом распределения, который является законом распределения непрерывной случайной величины.

4. Установим связь между параметром λ и интенсивностью µ для простейшего ПВ. Пусть t=1, следовательно, 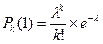. По определению 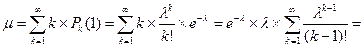[пусть n=k-1] 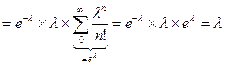. Следовательно, λ=µ. Данное равенство верно для любого стационарного потока, в том числе и для потока с последействием. Это равенство указывает на то, что простейший ПВ полностью описывается интенсивностью потока, то есть µ. На практике достаточно знать среднее число вызовов в единицу времени, чтобы определить все остальные характеристики простейшего потока, в том числе и вероятность Pk.

5. Определим математическое ожидание числа вызовов, поступающих за промежуток времени t. Обозначим интересующую нас величину k, k= 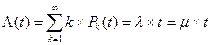. Следовательно, среднее число вызовов определяется выражением k= λt. Этому же значению соответствует и дисперсия числа поступающих вызовов: Dk= λt. Математическое ожидание характеризует среднее число вызовов, а дисперсия — меру разброса относительно этого среднего значения.

Среднеквадратическое отклонение (СКО): .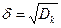

Таким образом, первый (k) и второй (Dk) моменты распределения дискретной случайной величины равны между собой.

 

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ПРОМЕЖУТКОВ ВРЕМЕНИ

МЕЖДУ ВЫЗОВАМИ

 

Рассмотрим другой способ описания простейшего потока при помощи функции распределения промежутков между вызовами A(x). Обозначим F(x) — вероятность того, что некоторая случайная величина z не превзойдет некоторое заданное значение х, где х — промежуток времени. F(x)=P{z≤x} — вероятность того, что в промежуток времени между двумя последовательными моментами поступления вызовов не превзойдет х. Эта вероятность равносильна вероятности поступления хотя бы одного вызова на промежутке [0;x). Следовательно, F(x)= π1(x)=π0(x)-P0(x)= [где: π0=0,1,2,...; P0=0; π0 - достоверное событие. Следовательно,] =1-e-λx [из формулы Пуассона]. Получаем: F(x)=1-e-λx, A(x)=F(x). Таким образом, F(x) подчиняется экспоненциальному (показательному) закону.

Только такая показательная функция обладает свойством отсутствия последействия (из дискретных распределений отсутствием последействия обладает геометрическое распределение).

Марковский процесс, обладающий свойством отсутствия последействия, характеризуется упрощенной математической моделью.

Исследуем функцию F(x) графически. Зафиксируем некоторую точку x1 и покажем три графика подобного вида.

 

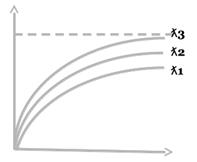
Чем больше λ, тем больше доля промежутков между вызовами будет иметь длительность меньше, чем x1. То есть, тем выше вероятность того, что за промежуток [0;x1) поступит хотя бы один вызов. Следовательно, λ1<λ2<λ3.

Выберем некоторую точку F*(x), опустим перпендикуляры из точек пересечения этих значений на ось x. Чем больше λ, тем меньше длина промежутка, который не будет превышен. Из анализа этих графиков виден физический смысл формулы для математического ожидания длины промежутка между вызовами: ż .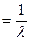

Таким образом, чем больше λ, тем меньше математическое ожидание длины промежутка между вызовами.

Дисперсия для промежутков между вызовами имеет следующее значение: 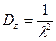, а среднеквадратическое отклонение .

 

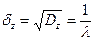ПОТОКИ С ПРОСТЫМ ПОСЛЕДЕЙСТВИЕМ

 

Пусть существует система РИ, на которую поступает ПВ. Пусть из системы выходит поток обслуженных вызовов, и система предоставляет поступающим вызовам свои ресурсы, например, соединительные пути.

 

 

 

Состояние системы S(t) — это такое состояние, при котором фиксированы каждый занятый и свободный ресурс системы в момент t, при этом известно, вызовы каких именно источников обслуживаются данной системой. Если в процессе исследования системы необходимо учитывать состояние, которое принимает система, то параметр поступающего ПВ определяется следующим образом: 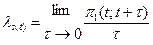, при условии, что в момент времени t, система находилась в состоянии S(t); где π1(t;t+τ) при S(t) — вероятность поступления за промежуток [t;t+τ) одного и более вызовов, если в момент времени t, система находится в состоянии S(t).

Рассмотрим среди потоков с последействием такие потоки, у которых это последействие является простым. Поток с простым последействием — это ординарный поток, для которого в любой момент времени существует конечный параметр потока состояния λs(t). Это параметр зависит только от состояния системы в момент времени t и не зависит от процесса обслуживания вызовов до момента времени t. Данный поток для определения λs(t) требует знания значения системы S(t) в этот момент. Также такой поток является нестационарным, так как в различные моменты времени t1,t2,... имеют место различные состояния S(t1),S(t2),... соответственно. Однако при t →∞ поток с простым последействием стремится к стационарному потоку.

Рассмотрим несколько частных случаев с простым последействием.

Симметричный поток — это такой поток с простым последействием, параметр которого λs(t) в любой момент времени t зависит только от числа установленных соединений i, то есть зависит от числа вызовов, которые обслуживаются системой в рассматриваемый момент t. Следовательно, для симметричного потока λs(t) = λi. Зависимость λi может быть различной.

Например, примитивный поток — это такой симметричный поток, параметр которого λi зависит от числа обслуживаемых системой вызовов, причем параметр λi прямо пропорционален числу свободных источников. λi = α (N-i) , где α — коэффициент пропорциональности, численно равный параметру одного источника; N — число источников вызовов; i — число занятых источников; N-i — число свободных источников.

Частным случаем примитивного потока является простейший ПВ. Простейший поток — это такой примитивный поток, параметр которого λi не зависит от состояния системы. λi = λ =const. Действительно, с увеличением N и с уменьшением α, последействие убывает. В предельном случае, когда N →∞ и α →∞, причем так, чтобы αN=const, параметр λ=αN не зависит от состояния системы и, при этих условиях, модель примитивного потока переходит в модель простейшего потока.

Среди потоков с простым последействием, интерес представляет также поток с повторными вызовами. Рассмотрим такие потоки более подробно. Действительно, система обслуживает не все поступающие вызовы. Часть из них не обслуживается по целому ряду причин. Например, занятость абонента, отсутствие абонента, неисправности, ошибки в наборе номера, и тому подобное. Если вызов теряется, то нередко источники необслуженных вызовов совершают повторные вызовы. То есть поток с повторными вызовами состоит как из первичных, так и из повторных вызовов. Оценим параметр повторных вызовов. Пусть поток первичных вызовов будет простейшим, с параметром λ. Параметр потока повторных вызовов определим через произведение 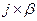, где j — число источников повторных вызовов, и β — интенсивность повторений, то есть параметр одного источника повторных вызовов. Тогда суммарный поток λповт.в. = λ +j β. Если поток первичных вызовов является примитивным, то для потока с повторными вызовами верно: λповт.в. = α(N-i-j) +j β.

 

Часть 2

 

ВРЕМЯ ОБСЛУЖИВАНИЯ

 

Процесс обслуживания описывается символом B(x) на второй позиции в классификации Кендалла. Процесс обслуживания характеризуется определенной длительностью. Эта длительность может быть как случайной, так и детерминированной. В соответствии с этим, рассмотрим наиболее распространенные функции распределения длительности обслуживания.

1) Показательное распределение длительности обслуживания. Многие реальные функции распределения подчиняются показательному закону. В частности, показательное распределение хорошо описывает длительность телефонного разговора и другие подобные процессы. Показательное распределение обладает таким свойством, как полное отсутствие последействия. Математически это дает значительные преимущества, так как позволяет пользоваться теорией марковских процессов, в которых будущее не зависит от прошлого и определяется известным настоящим. Рассмотрим выражение для функции распределения длительности обслуживания: B(x)=P{t≤x}=1-e- β x, где β — интенсивность освобождения вызовов (параметр функции распределения B(x)); B(x) — вероятность того, что длительность обслуживания t будет меньше, или равна некоторому, наперед заданному, времени x. Математическое ожидание (среднее время обслуживания): ŧ 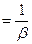. Дисперсия (мера разброса, относительно среднего значения): 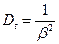. Среднеквадратическое отклонение: .

 

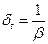Рассмотрим график B(x):

 

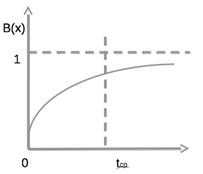
На этом графике на оси абсцисс выделим некоторую точку, назовем ее tср. Построим перпендикуляр из этой точки. Площади, которые образуются слева и справа, будут равны друг другу. С целью упрощения математических расчетов, обычно за единицу времени принимают среднюю длительность обслуживания ŧ =1. В этом случае, β =1, а B(x)=1-e-x.

2) Детерминированное распределение. Данное распределение также широко используется, например, для описания процессов обслуживания пакетов, или сообщений фиксированной длины. В этом случае .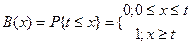

Графически это можно изобразить так:

 

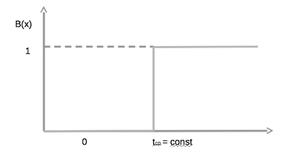
Детерминированное распределение значительно усложняет математический аппарат, так как свойство марковости здесь не наблюдается. Обе функции распределения: и показательная, и детерминированная, являются предельными случаями распределения и относятся к так называемым k-распределениям Эрланга.

 

НАГРУЗКА

 

Доставка и обработка информации в системе характеризуется определенной работой этой системы.

Можно рассмотреть три вида этой работы:

1. Работа, вносимая в систему (поступающая нагрузка).