2. Источники вызовов создают ПВ, поступающих в обслуживающую систему.
ТЕОРИЯ ТЕЛЕТРАФИКА
Курс лекций для СДО
(Три части и три теста, итоговый зачет и курсовая работа)
Текст лекций
Часть 1
ВВЕДЕНИЕ
Связь развивается в соответствии с законами, по которым происходит передача и обработка информации. Передача и обработка информации включает ее декодирование, запоминание, хранение, извлечение, тиражирование и другие преобразования. Для выбора оптимальных вариантов в области связи важное значение имеют вопросы, которыми занимаются три теории, связанные с передачей и обработкой информации: «теория передачи информации» (ТПИ), «теория обработки информации» (ТОИ), «теория распределения информации» (ТРИ). Теория телетрафика (ТТТ) является важной частью ТРИ, которая разрабатывает методы построения, расчета и функционирования систем и сетей связи. Можно сказать, что ТРИ распределяет ресурсы между пользователями. В качестве ресурсов обычно рассматриваются каналы связи, средства коммутации, средства управления (память) и другие.
ТРИ имеет три основных раздела:
1) теория структур, которая занимается конструированием системы распределения информации;
2) теория управления, которая обеспечивает управление сетями, в том числе и распределение информационных потоков в сетях;
3) теория телетрафика, которая исследует вероятностные процессы функционирования цепей и узлов связи.
Понятие «телетрафик» - составное: «теле» - греч. «далеко», «трафик» - англ. «передача, нагрузка». Таком образом, телетрафик соответствует понятию, связанному с сообщениями в информационной сети, которые передаются на определенное расстояние. Пример понятия, с которым оперирует телетрафик: передача определенного объема данных.
ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ТЕЛЕТРАФИКА
ТТТ решает 4 группы задач (1-3 — анализ, 4 — синтез). Рассмотрим их.
1) Полезный эффект в работе информационных сетей заключается в доставке информации. Всякое сообщение передается в информационную сеть в случайный или детерминированный (определенный) момент времени. Если рассматривать только моменты поступления сообщения, то можно говорить о потоках (пачках) вызовов (вызовы или требования, заявки). Потоки вызовов (ПВ) могут иметь различную структуру, различную интенсивность (частоту) и другие параметры. Большинство ПВ подвержены случайным колебаниям (колебаниям сложного характера). Так, например, потоки телефонных вызовов колеблются по дням недели, часам суток, имеют место случайные колебания по сезонам, и так далее.
2) Доставка информации неизбежно влечет за собой дополнительные процессы. Например, не каждый телефонный вызов завершается разговором, так как абонент может не ответить, или быть занят, или произошла ошибка в наборе номера, технические причины, отсутствие свободных ресурсов, и так далее. Однако, независимо от исхода, каждая попытка обслуживания приводит к занятию определенных ресурсов системы, при этом создается так называемая нагрузка на коммутационные устройства и устройства управления. Нагрузка характеризует интенсивность обмена информацией между потребителями. Нагрузка определяется интенсивностью поступления вызовов, а также длительностью занятия вызова элементов соединительного тракта. Таким образом, вторая задача ТТТ состоит в изучении нагрузки, создаваемой потоком вызовов (ПВ).
3) По нагрузке, создаваемой поступающими вызовами, по характеру ее распределения во времени и с расчетом допустимого качества обслуживания, определяется необходимый объем оборудования как для коммутации, так и для управления. В этом состоит еще одна важная задача ТТТ. При этом под качеством обслуживания обычно понимается некоторая функция потерь. Также при решении задачи определения объема оборудования, учитывается порядок приема вызовов на обслуживание (таких алгоритмов достаточно много, например, FIFO, LIFO). Также в технике связи учитываются дисциплины обслуживания (ДО): с потерями, с ожиданием, с повторными вызовами, и так далее.
4) Задача установления закономерностей между ПВ, нагрузкой и объемом оборудования, с тем, чтобы обеспечить удовлетворительное качество обслуживания при наименьшем объеме оборудования, для оптимального построения новых систем и сетей связи (задача синтеза).
ТТТ как дисциплина имеет международный статус и тесно связана с такими теориями, как теория массового обслуживания, теория вероятностей, математическая статистика, теория случайных процессов, комбинаторика, и так далее.
В развитие ТТТ большой вклад внесли российские ученые, такие как
А.Н. Колмогоров, А.Я. Хинчин, А.Д. Харкевич, Б.С. Лившиц. Среди зарубежных ученых следует выделить Эрланга, Пальма, Энгсета, Кроммелина. Основные результаты ТТ были получены в начале 20 века.
МОДЕЛЬ ОБСЛУЖИВАНИЯ ОБЩЕГО ВИДА
В теории массового обслуживания рассматривается следующее представление любой системы, которая принимает и обрабатывает информацию. Такая модель также рассматривается и в ТТТ. Рассмотрим ее элементы.
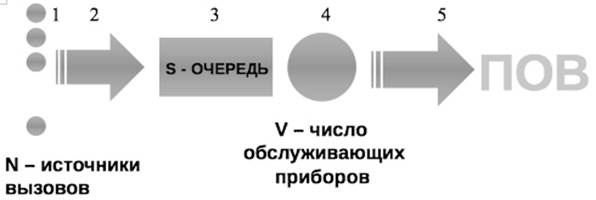
1. N — источники вызовов.
2. Источники вызовов создают ПВ, поступающих в обслуживающую систему.
3. Вызовы поступают в очередь, где S — число мест для ожидания.
4. Обслуживающий прибор(ы), число которых равно V (например, число операторов системы или число линий в пучке).
5. Поток обслуженных вызовов — ПОВ.
Для описания таких систем широко распространено пятисимвольное обозначение, которое применимо к любой системе массового обслуживания. Такое обозначение носит название классификации Кендалла:
A/B/V/K/N
A — процесс, характеризующий поступление вызовов. Этот процесс записывается в виде функции распределения промежутков между вызовами A(x), где x — длина промежутка (длительность).
B — процесс, характеризующий процесс обслуживания вызова. Описывается через функцию распределения длительности обслуживания B(x), где x — длительность обслуживания.
V — количество обслуживающих приборов:
Min=1 — однолинейная система обслуживания;
Max= ∞ — немедленная система обслуживания.
K=S+V — емкость накопителя системы.
N — число источников (заявок, вызовов, требований).
Некоторые позиции в классификации могут принимать значения бесконечность, либо вообще отсутствовать, если этот символ последний.
Примеры: A/B/V/ ∞ /N — система с бесконечной очередью;
A/B/V — бесконечное число источников с бесконечной очередью.
Процессы A и B могут относиться к классу случайных или марковских процессов. В этом случае в классификации это отображается символом «M»: M/M/V/K/N.
Марковский процесс характеризуется свойством: будущее не зависит от прошлого процесса и определяется только его настоящим. Если функция распределения обладает этим свойством, то она имеет вид показательного (экспоненциального) распределения: eµt.
Еще один вид закона распределения — детерминированная функция распределения: D/D/V.
С точки зрения обслуживания, детерминированное распределение вычислительно менее удобно, поэтому такие модели чаще рассчитываются с помощью численных методов. Если процесс определить трудно, то он считается процессом общего вида и обозначается: G/G/V/K/N — наихудший случай для расчета (самый сложный).
ДИСЦИПЛИНЫ ОБСЛУЖИВАНИЯ (ДО) В ИНФОРМАЦИОННЫХ СЕТЯХ
В телекоммуникационных системах наибольшее распространение получили три модели обслуживания:
1. ДО с отказами и повторными вызовами
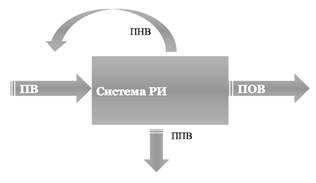
РИ — распределение информации
ПВ — поток вызовов
ПНВ — поток необслуженных вызовов
ПОВ — поток обслуженных вызовов
ППВ — поток потерянных вызовов.
Система РИ представляет вызовам свои ресурсы (места в очереди, обслуживающие приборы). Часть вызовов успешно обслуживается и образует ПОВ. Другая часть образует ППВ, а еще одна часть формирует ПНВ, который возвращается на вход системы. Источник вызова в случае неуспешного обслуживания может послать повторный вызов с целью установки этой самой связи. Например, телефонные абоненты, в случае занятости вызываемого абонента, обычно проявляют настойчивость и организуют серию повторных вызовов. Данная модель является наиболее реальной, то есть хорошо отражает действительную ситуацию. На одно успешное соединение приходится 2-4 повторных вызова. Эту модель можно использовать для расчетов параметров системы, которая обеспечивает передачу как речевой информации, так и данных. На практике используется достаточно редко из-за математической сложности.
2. ДО с потерями
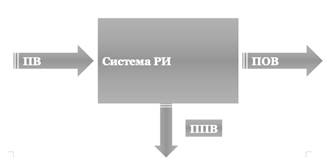
Данная модель характеризуется тем, что вызов, поступивший в момент занятости ресурсов, получает отказ. В такой системе каждый вызов, в том числе и повторный, воспринимается как новый. Модель удобна для расчета оборудования системы с ограниченными ресурсами. Многие реальные модели вполне соответствуют данной, а математический аппарат значительно проще.
3. ДО с ожиданиями
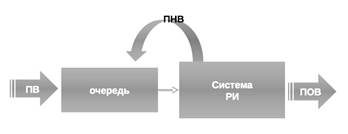
В данной модели нет явных потерь вызовов, так как любой вызов при отсутствии ресурсов будет ожидать обслуживания. Процесс обработки информации начинается с того, что вызов, не найдя свободных ресурсов, становится в очередь; по мере освобождения ресурсов вызов получит обслуживание. В случае неуспешного обслуживания, вызов возвращается на вход в систему, то есть может снова встать в очередь. Данная дисциплина широко используется, в частности, для расчета управляющих устройств в системах с коммутацией пакетов и коммутацией сообщений.
ПОТОКИ ВЫЗОВОВ (ПВ)
ПВ связаны с процессом доставки информации в систему и характеризуются в классификации Кендалла функцией распределения длительности промежутков между вызовами A(x).
ПВ — это последовательность вызовов, поступающих в детерминируемые или случайные моменты времени при непрерывном течении этого времени.

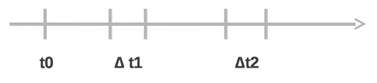
Удобно графически представлять ПВ в виде графического изображения с последовательно расположенными точками t. t0 — момент начала отсчета.
Через z1,z2,z3,… обозначим промежутки между моментами поступления вызовов. Момент времени — число, соответствующее промежутку времени от начала отсчета t0 до рассматриваемой точки на оси времени. Моментов времени бесконечно много.
Вызывающий момент времени — момент времени, в который поступает то или иное число вызовов.
Существует три эквивалентных способа задания ПВ:
1) При помощи моментов поступления вызовов ti. t0,t1,t2,….
2) При помощи промежутков между вызовами z1,z2,… (z0 не существует).
3) При помощи последовательности чисел k1,k2,… , характеризующих количество вызовов, поступающих на отрезки времени [0, t1), [0, t2), [0, t3).
Эквивалентность способов задания ПВ состоит в том, что если ПВ задан при помощи одного из них, то эти описания позволят описать его и двумя другими способами.
ОСНОВНЫЕ СВОЙСТВА ПВ
Реальные ПВ обладают свойствами, которые помогают упростить описание этих потоков. К их числу относятся: стационарность, ординарность, наличие или отсутствие последействий.
1. Стационарность.
Стационарный ПВ — это такой поток, в котором характер поступления вызовов на некотором промежутке времени зависит от длины этого промежутка, но не зависит от того, где на оси времени этот промежуток находится.
Таким образом, ПВ можно назвать стационарным, если вероятность поступления того или иного числа вызовов на некотором промежутке времени для случайного потока, или число вызовов на некотором промежутке времени для детерминированного потока, зависит от длины промежутка и не зависит от того, где на оси времени этот промежуток находится. Таким образом, стационарность ПВ означает независимость его вероятностного режима от времени.
Любой стационарный случайный ПВ можно задать семейством условных вероятностей Fk( τ ), где k=0,1,2,... поступления k вызовов на некотором отрезке времени τ.
ПВ называется нестационарным, если для случайного ПВ вероятность поступления некоторого числа вызовов за заданный промежуток времени зависит как от длины этого промежутка, так и от того, где на оси времени этот промежуток расположен.
Рассмотрим примеры потоков, которые обладают или не обладают свойством стационарности.
- ПВ, поступающих на телефонную станцию в течение суток.
Очевидно, что в дневные часы суток интенсивность поступаемого ПВ больше, чем в ночное время. Следовательно, такой ПВ является нестационарным.
2. Но если ограничить наблюдения за данным ПВ меньшим временем, то с приемлемой для практики точностью такой поток можно считать стационарным. Для этого принято рассматривать час наибольшей нагрузки (ЧНН). ЧНН — это непрерывный интервал времени в 60 минут, в течение которого интенсивность нагрузки, оцениваемая как время занятия приборов системы обслуживания, является наибольшей.
2. Последействие.
ПВ называется потоком без последействия, если вероятность поступления того или иного числа вызовов на некотором отрезке врем до ени не зависит от процесса поступления вызовов до момента наблюдения. То есть, не зависит от того, в какие моменты времени и сколько вызовов поступило до начала момента наблюдения. Таким образом, для потока без последействия прошлая история потока не играет никакой роли для предсказания его будущего.
Поток без последействия можно задать с помощью функции распределения Fk(t1,t2), где: k=0,1,2,...; где Fk (t1,t2) - условная вероятность поступления k-вызовов на промежутке времени от t1 до t 2, вычисленная при любом предположении о течении процесса обслуживания до момента t1 (точки начала наблюдения). Это значит, что такая вероятность равна безусловной вероятности, и подобный поток можно задать семейством вероятностей Pk(t1,t2) = Fk(t1,t2) .
Если поток без последействия стационарен, очевидно, что его можно задать семейством безусловных вероятностей Pk (t), то есть вероятность поступления вызовов для стационарного потока не зависит от начала отсчета, следовательно, момент начала отсчета не учитывается; где t — длина промежутка наблюдения.
На практике существуют потоки с последействием, среди которых выделяют потоки с частичным последействием. В классе потоков с частичным последействием наиболее значимыми являются потоки с простым последействием. Простое последействие означает, что вероятность за бесконечно малый промежуток времени [t,t+ τ ), где τ → 0, определяется состоянием системы в момент времени t. При этом под состоянием системы понимается полная информация о том, какие входы и выходы системы заняты.
Примеры:
1) ПВ на телефонную станцию при большой емкости узла можно считать ПВ без последствия. Если емкость узла составляет порядка 10000 абонентов, то при нормальном уровне нагрузки в соединении участвуют от 10 до 20% абонентов. Это статистические данные. Это означает, что поведение абонентов можно рассматривать как независимое. Причем не только от поведения других абонентов, но и от того, каким был процесс поступления вызовов до начала момента наблюдения. И этот процесс не зависит от того, в каком состоянии находится обслуживающая система.
2) ПВ от спаренного телефонного аппарата. В подобных случаях поступление вызова от одного абонента зависит, в каком состоянии находится другой абонент. Такой ПВ обладает последействием.
3) ПВ от абонентов офисной станции для выхода в город. Так как данный поток является потоком от ограниченного числа источников, то состояние системы до момента наблюдения является существенным для предоставления обслуживания других абонентов. Это ПВ с последействием.
4) Вызовы на перегруженное направление. Это также ПВ с последействием, так как ситуация зависит от того, в какой момент происходит обращение к системе.
3. Ординарность.
Возьмем некий отрезок [t,t+ τ ) и обозначим через π k [t,t+ τ ) вероятность поступления k и более вызовов на отрезке времени [t,t+ τ ). ПВ называют ординарным, если вероятность поступления двух и более вызовов на отрезке [t,t+ τ ) при τ → 0 есть бесконечно малая величина большего порядка малости, чем τ. То есть: π2 (t,t+ τ )=o( τ ), при τ → 0. Такая запись эквивалентна следующему пределу: 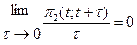 .
.
Практически ординарность потока означает невозможность поступления двух и более вызовов в любой момент времени t.
ПВ называют неординарным, если в каждый вызывающий момент времени возможно поступление более одного вызова. Например, телефонный вызов можно считать ординарным, однако встречаются неординарные вызовы, например, при конференц-связи, групповой рассылке и пр.
ХАРАКТЕРИСТИКИ ПВ
Основными характеристиками ПВ являются:
1. Ведущая функция потока
2. Интенсивность потока.
3. Параметр потока.
Рассмотрим их подробнее.
1. Ведущая функция потока Λ (t) — математическое ожидание числа вызовов в интервале времени [0;t). Очевидно, что функция Λ(t) - неотрицательная, неубывающая, в практических задачах имеет конечное значение.
2. Интенсивность потока. Различается для стационарного и нестационарного потоков. Нестационарный поток характеризуется мгновенной интенсивностью µ (t) в момент времени t; она определяется так:
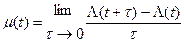 .
.
Это скорость изменения величины в момент времени t.
Стационарный поток характеризуется средней интенсивностью µ, то есть математическим ожиданием числа вызовов в единицу времени.
Размерность для измерения интенсивности обратно пропорциональна времени: 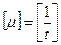 . За единицу времени можно выбрать час, минуту, секунду. Часто в качестве единицы времени выбирается средняя длительность одного обслуживания, что приводит к упрощению вычислений. Очевидно, для стационарного потока справедливо равенство: Λ (t)= µt.
. За единицу времени можно выбрать час, минуту, секунду. Часто в качестве единицы времени выбирается средняя длительность одного обслуживания, что приводит к упрощению вычислений. Очевидно, для стационарного потока справедливо равенство: Λ (t)= µt.
3. Параметр потока λ(t) для некоторого случайного потока в момент времени t определяется как предел отношения вероятности поступления хотя бы одного вызова на интервале времени [t,t+ τ) к длине этого интервала, при стремлении этой длины к нулю: 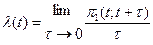 . (*)
. (*)
Параметр случайного потока λ(t) определяет в момент времени t плотность вероятности поступления вызывающего момента, то есть выражение (*) эквивалентно следующему равенству: 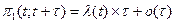 , при τ →0. (**)
, при τ →0. (**)
Согласно определению стационарного потока, вероятность поступления определенного числа вызовов за некоторый промежуток времени одна и та же, независимо от места, где расположен этот промежуток. Следовательно, плотность вероятности для стационарного потока есть величина постоянная, не зависящая от времени. То есть для случайных стационарных потоков λ(t)=λ и (**) приобретает вид: 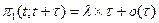 при τ →0.
при τ →0.
Чтобы лучше понять различия между характеристиками стационарного потока µ и λ, рассмотрим следующий пример:
Пусть есть два ПВ, моменты вызовов которых совпадают: 1 — ординарный ПВ, 2 — неординарный ПВ. Для 1-го ПВ в каждый вызывающий момент поступает один вызов, для 2-го — по два.
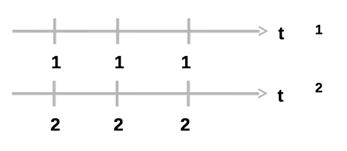
Так как вызывающие моменты потоков совпадают, то λ1=λ2. Однако очевидно, что интенсивности µ1<µ2. Таким образом, параметр потока характеризует не ПВ в целом, а только поток вызывающих моментов.
ОСНОВНЫЕ ХАРАКТЕРСТИКИ ПВ
Информацию по характеристикам ПВ сведем в итоговую таблицу.
| Нестационарный поток | Λ(t) | µ(t) | λ(t) |
| Стационарный поток | µt | µ | λ |
ПРОСТЕЙШИЙ ПВ
Простейший ПВ — это основная математическая модель для потока, действующего в информационных системах. В качестве примера рассмотрим ПВ, поступающий на узел коммутации подвижных станций. Такой поток создается большим источником вызовов, на практике, это когда N>100, благодаря этому действие источников вызовов можно рассматривать как независимое, а это значит, что такой реальный поток, с достаточной для практики точностью, можно рассматривать как поток без последействия. Если предположить, что каждый источник может генерировать только один вызов, то такой поток обладает свойством ординарности. Если ограничить наблюдение за потоком рамками ЧНН, то такой поток можно рассматривать как стационарный. Совокупность рассмотренных свойств определяет математическую модель простейшего ПВ.
Простейший поток — это стационарный ординарный поток без последействия.
Простейший ПВ можно описать двумя способами:
1. При помощи функции распределения промежутков между вызовами A(x).
2. При помощи функции распределения числа событий потока, которые происходят на отрезке от 0 до t. То есть для описания потока можно использовать вероятность поступления вызовов на данном промежутке t: Pk (t), [0;t), где k=0,1,2,.. .
Рассмотрим сначала второй способ описания потока. Для этого рассмотрим вероятность Pk (a;a+t) — вероятность поступления точно k вызовов на промежутке времени [a;a+t). Представим промежуток [a;a+t) состоящим из двух частей и добавим a+t+ τ . Образуется промежуток [a;a+t+ τ)=[a;a+t)+[a+t;a+t+τ). Для определения вероятности Pk (t) будем последовательно использоваться свойства простейшего ПВ:
1. Воспользуемся свойством стационарности. Согласно этому свойству, вероятность поступления некоторого числа вызовов на промежутке времени зависит от длины этого промежутка и не зависит от того, где на оси времени расположен этот промежуток. Следовательно, можно упростить введенные обозначения и записывать их следующим образом:
[a;a+t+ τ) →[t+τ)
[a;a+t)→[t)
[a+t;a+t+τ)→[τ)
Рассмотрим все возможные события, которые приводят к тому, что на большом промежутке [t+τ) поступит точно k вызовов. Чтобы это произошло, необходимо, чтобы на промежутке t поступило: k, или k-1, или k-2, или 0 вызовов, а на промежутке τ соответственно: 0, или 1, или 2, …, или k вызовов. То есть:
| t+ τ | t | τ |
| k k k . . . k | k k-1 k-2 . . . 0 | 0 1 2 . . . k |
На рассматриваемых промежутках происходит только появление (рождение) вызовов, в терминах марковских процессов такой процесс называют процессом чистого размножения.
2. Рассмотрим свойство отсутствия последействия. Оно указывает на то, что события, происходящие на отрезках t и τ, являются независимыми. Эти события являются несовместимыми (соединяются через «или»). Следовательно, можно за каждой реализацией записать следующее выражение: 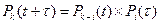 , где i=0,1,2,...,k. Здесь, Pk (t+ τ) — вероятность поступления точно k вызовов за промежуток времени t+ τ. Учитывая, что рассмотренные события являются независимыми, можно воспользоваться формулой полной вероятности ФПВ (Формула Байеса):
, где i=0,1,2,...,k. Здесь, Pk (t+ τ) — вероятность поступления точно k вызовов за промежуток времени t+ τ. Учитывая, что рассмотренные события являются независимыми, можно воспользоваться формулой полной вероятности ФПВ (Формула Байеса): 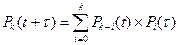 , где k=0,1,2,... (*)
, где k=0,1,2,... (*)
3. Воспользуемся свойством ординарности. С этой целью устремим τ к нулю. В соответствии с определением для ординарного ПВ вероятность поступления двух и более вызовов на промежутке π 2 ( τ ), есть бесконечно малая величина большего порядка малости, чем τ, то есть: π 2 ( τ )=o( τ). Следовательно, тем более бесконечно малым является поступление точно двух вызовов P2( τ)=o(τ), точно трех вызовов P3( τ)=o(τ), и так далее.
Таким образом, при τ→0 в выражении (*) появляются бесконечно малые величины. Просуммировав эти бесконечно малые величины, вынесем их за знак суммы. При этом выражение примет вид: 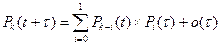 (**), где τ→0; k=0,1,2,... . Сделаем дальнейшие преобразования:
(**), где τ→0; k=0,1,2,... . Сделаем дальнейшие преобразования:
Pk (t+ τ )=Pk-1(t)P1( τ )+Pk(t)P0( τ )+o( τ ), где τ →0; k=0,1,2,... .
В полученном выражении определим величины P1( τ) и P0(τ). Можно записать, что P1( τ)=π1(τ)-π2(τ), при τ→0.
Вероятность π1(τ) определим, исходя из значения параметра простейшего потока. 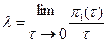 , заданное выражение эквивалентно следующей записи: π1(τ)=λτ+o(τ). Исходя из свойства ординарности, π2(τ)=o(τ), при τ→0. Таким образом, P1( τ )=λτ+o(τ).
, заданное выражение эквивалентно следующей записи: π1(τ)=λτ+o(τ). Исходя из свойства ординарности, π2(τ)=o(τ), при τ→0. Таким образом, P1( τ )=λτ+o(τ).
Определим P0( τ), рассуждая аналогично, запишем: P0( τ)=π0(τ)-π1(τ), при τ→0. π0(τ) — вероятность достоверного события, которая равна единице, то есть π0(τ) =1. Соответственно, выражения для P0( τ) приобретают следующую форму: P0( τ )=1-(λτ+o(τ))=1-λτ+o(τ), при τ→0.
Подставим выражения P1( τ) и P0( τ) в преобразованное выражение (**): Pk (t+ τ)=Pk-1(t)(λτ+o(τ))+Pk(t)(1-λτ+o(τ))+o(τ), где: τ→0; k=0,1,2,... .
Перенесем в левую часть уравнения вероятность Pk (t) и поделим обе части на τ: 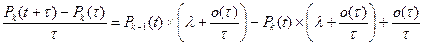 , где: τ→0; k=0,1,2,... .
, где: τ→0; k=0,1,2,... .
Перейдем к пределу, при этом в левой части выражения для каждого выражения получим производную от t, а выражение 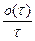 обратится в ноль. Получим окончательное выражение:
обратится в ноль. Получим окончательное выражение: 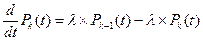 , где: k=0,1,2,... .
, где: k=0,1,2,... .
Получилась система из бесконечно большого числа дифференциальных уравнений. Существуют различные методы решения этой системы. Одним из удобных способов является метод производящих функций. Результатом решения данной системы является следующая формула:
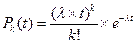 — формула Пуассона, где k=0,1,2,... .
— формула Пуассона, где k=0,1,2,... .
Итак, мы рассмотрели процесс чистого размножения, который описывается формулой Пуассона. Его также называют стационарным Пуассоновским процессом. Следовательно, простейший ПВ называют стационарным Пуассоновским потоком.
ХАРАКТЕРИСТИКИ ПРОСТЕЙШЕГО ПВ
1. При объединении n независимых простейших ПВ с параметрами λ1,λ2,...,λn получается общий суммарный, также простейший поток вызовов с параметрами λƩ=λ1,λ2,...,λn.
Объединение большого числа стационарных ординарных потоков с практически любым последействием, при малых значениях параметров этих потоков, создает общий поток, близкий к простейшему.








