Задачи по теме Графы
15.02.2023 Статистика
Задачи по теме Графы
Графы – замечательные математические объекты, с их помощью можно решать много различных, внешне не похожих друг на друга задач.
Граф – это набор точек, некоторые из которых соединены линиями. Могут соединяться не все точки друг с другом и соединяются не обязательно отрезками, а произвольными линиями-дугами. Примеры – наглядные рисунки.
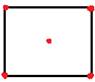
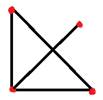
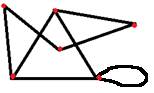

 рис.1 рис.2 рис.3 рис.4 рис.5
рис.1 рис.2 рис.3 рис.4 рис.5
Основные понятия: вершины (точки) и ребра (линии, соединяющие вершины) графа. Четкого, строгого обозначения вершин не существует, обозначают из контекста задачи: или буквами (русскими, латинскими) или цифрами. Причем нужно особо подчеркнуть, что бывают графы, состоящие только из одних вершин (рис.5), что две вершины могут быть соединены несколькими ребрами одновременно (рис.4) и что ребро может «выходить и заходить» в одну и ту же вершину (рис.3) – такое ребро называют петлей.
Графы используются не только в математике, но могут быть «нематематические графы». Так, например, люди часто пользуются графами, не догадываясь об этом, когда изображают различные объекты: населенные пункты, карты городов, схемы электроприборов, атомы. Схема метро это тоже граф: вершины конечные станции и станции пересадок, ребра – пути, соединяющие эти станции. Дворянство тоже применяло графы для создания генеалогического дерева. В них вершины – это члены рода, а связывающие их линии - отношения родственности, ведущие от родителей к детям. Ниже приведен фрагмент родословной А.С. Пушкина.
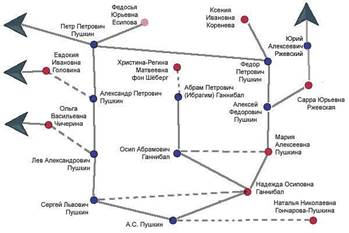
Графы бывают конечные (число его ребер конечно) и бесконечные (число его ребер бесконечно).
Степень вершины – число ребер выходящих из вершины графа. Если ребро является петлей, то его считают дважды. Закрепляем определение примерами: на рис 1 изображен граф, который имеет
Вершин – 5,
Ребер – 4.
Степень вершин (надо пронумеровать все вершины (например вершины прямоугольника 1, 2, 3,4 – степень 2, 5 – степень - 0).
Иногда степень вершины записывают в виде таблицы, а иногда пишут рядом с самой вершиной. Важно подчеркнуть, что одно и тоже ребро считается дважды (один раз – для одной вершины, второй – для другой), так как оно соединяет две вершины.
Вершины бывают четные (степень вершины четна) и нечетные (степень вершины нечетна).
Домашнее задание.
1. Построить граф, определить по рисунку, сколько вершин, ребер у граф, какова степень вершины графа, посчитать сколько четных и нечетных вершин.

рис.7








