Метод алгебраического сложения
Метод подстановки
Теория:
Алгоритм решения системы двух уравнений с двумя переменными x,y методом подстановки:
1. Выразить одну переменную через другую из одного уравнения системы (более простого).
2. Подставить полученное выражение вместо этой переменной в другое уравнение системы.
3. Решить полученное уравнение и найти одну из переменных.
4. Подставить поочередно каждый из найденных на третьем шаге корней уравнения в уравнение, полученное на первом шаге и найти вторую переменную.
5. Записать ответ в виде пар значений, например, (x;y), которые были найдены соответственно на третьем и четвёртом шаге.
Пример:
Решить систему уравнений {xy=6 x−y=5
Решение.
1. Выразим x через y из второго (более простого) уравнения системы x=5+y.
2. Подставим полученное выражение вместо x в первое уравнение системы (5+y)⋅y=6
3. Решим полученное уравнение:
(5+y)y=65y+y2−6=0y2+5y−6=0y1=−6,y2=1
4. Подставим поочерёдно каждое из найденных значений y в уравнение x=5+y, тогда получим:
если y1=−6, то x1=5+(−6)=5−6=−1,
если y2=1, то x2=5+1=6.
5. Пары чисел (−1;−6) и (6;1) — решения системы.
Ответ: (−1;−6) и (6;1)
Метод алгебраического сложения
Теория:
Алгоритм решения системы двух уравнений с двумя переменными x,y методом сложения:
1. Уравнять модули коэффициентов при одном из неизвестных.
2. Сложить или вычесть уравнения.
3. Решить полученное уравнение с одной переменной.
4. Подставить поочерёдно каждый из найденных на третьем шаге корней уравнения в одно из уравнений исходной системы, найти второе неизвестное.
5. Записать ответ в виде пар значений, например, (x;y), которые были найдены.
Пример:
Решить систему уравнений {x2−y2=21 x2+y2=29
Решение.
Сложим уравнения.
{x2−y2=21 x2+y2=29+21 2x2=50
Решим полученное уравнение с одной переменной.
2⋅x2=50|:2x2=25x=±5
Подставим поочередно каждый из найденных корней уравнения
в одно из уравнений исходной системы, например во второе, и найдём второе неизвестное.
x2+y2=29
| если x=−5, то | если x=5, то |
| (−5)2+y2=29 25+y2=29 y2=29−25 y2=4 y1=−2,y2=2 | 52+y2=29 25+y2=29 y2=29−25 y2=4 y3=−2,y4=2 |
Пары чисел (−5;−2), (−5;2), (5;−2) и (5;2) — решения системы.
Ответ: (−5;−2), (−5;2), (5;−2) и
Метод введения новых переменных
Теория:
При решении систем двух уравнений с двумя переменными метод введения новых переменных можно применять двумя способами:
1. вводится одна новая переменная и используется только в одном уравнении системы;
2. вводятся две новые переменные и используются одновременно в обоих уравнениях системы.
Рассмотрим второй способ на примере.
Пример:
Решить систему уравнений {xy(x+y)=6 xy+(x+y)=5
Решение.
Введём новые переменные xy=u, x+y=v.
Тогда систему можно переписать в более простом виде:
{uv=6 u+v=5
Решением системы являются две пары чисел:
| {u1=2 v1=3 | {u2=3 v2=2 |
Вернёмся к переменным x и y и решим системы методом подстановки, тогда:
| {xy=2 x+y=3 {xy=2 x=3−y1.(3−y)y=2−y2+3y−2=0|⋅(−1)y2−3y+2=0y1=2,y2=12.x=3−yx1=3−2=1x2=3−1=2 | {xy=3x+y=2{xy=3x=2−y(2−y)y=3−y2+2y−3=0D<0∅ |
Ответ: (1;2) и (2;1)
Графический метод
Теория:
Алгоритм решения системы двух уравнений с двумя неизвестными графическим методом:
1. строим график первого уравнения;
2. строим график второго уравнения;
3. находим точки пересечения графиков (координаты каждой точки пересечения служат решением системы уравнений).
Пример:
Решить систему уравнений {x2+y2=9 y−x=−3
Решение.
1. Построим график уравнения x2+y2=9.
Графиком уравнения является окружность с центром в начале координат и радиусом 3.
2. Построим график уравнения y=x−3 (выразили y).
Это прямая, для построения которой найдём две точки (0;−3) и (3;0).
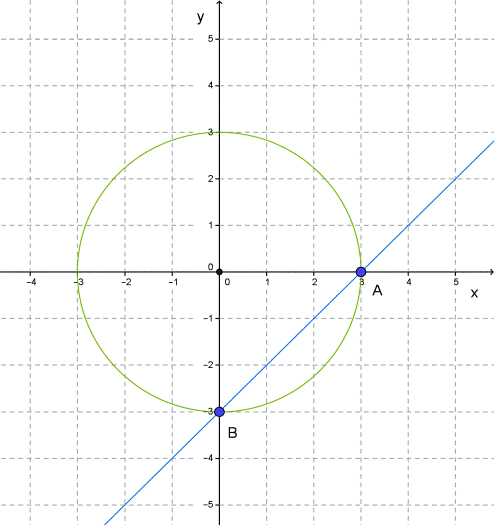
3. Окружность и прямая пересекаются в точках A и B.
Точка A имеет координаты (3;0), а точка B — координаты (0;−3).
Пары чисел (3;0) и (0;−3) являются решениями обоих уравнений системы, а значит, и решениями системы уравнений.
Ответ: (3;0) и (0;−3).








