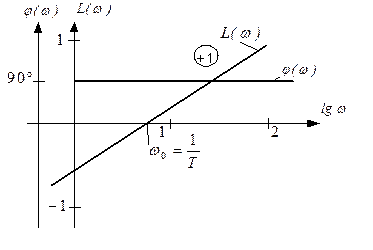Инерционное (апериодическое) звено 1 – го порядка
1. Передаточная функция (1 стр 1)
Если на вход любой системы подать сигнал синусоидальной формы:
x вх(t) = Xm cos(wt) = Xm e jwt .
Очевидно, что выходной сигнал будет иметь ту же форму:
x вых(t) = Ym cos(wt+j) = Ym e j(wt+j) .
Зависимость же между амплитудами и фазами выходного и входного сигналов определяет ДУ движения системы. Возмем произвольное, считая помеху f(t) равной нулю:
(T22 p2 + T1 p + 1) x вых(t) = (k1 + k2 p) x вх(t) .
Подставим сигналы в уравнение движения:
T22(jw)2 X вых e j(wt+j) + T1(jw) X вых e j(wt+j) + X вых e j(wt+j) = k1 Xвх e jwt + k2(jw) Xвх e jwt .
Найдем отношение выходного сигнала ко входному:
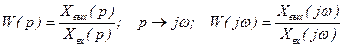 .
.
Вывод 1: Частотная передаточная функция получается из обычной заменой оператора Лапласа s на комплексную частоту jw, т.е. в результате перехода от изображения Лапласа к изображению Фурье.
Вывод 2: ДУ движения системы связывает входной и выходной сигналы (т.е. функции времени), ПФ связывет изображения Лапласа тех же сигналов, а частотная ПФ связывает их спектры.
Частотная передаточная функция может быть представлена в следующих видах:
W(jw) = A(w) e jj(w), или W(jw) = P(w) + j Q(w) ;
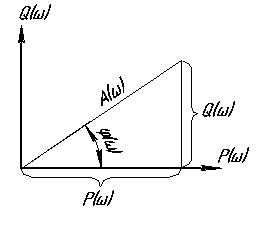 где: W(jw) – амплитудно-фазовая частотная характеристика (АФЧХ);
где: W(jw) – амплитудно-фазовая частотная характеристика (АФЧХ);
- A(w) - модуль частотной передаточной функции - находится как отношение модулей числителя и знаменателя (АЧХ):
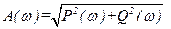
- j(w) - фаза частотной передаточной функции - находится как разность аргументов числителя и знаменателя (ФЧХ):
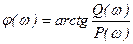
- P(w) и Q(w) - вещественная и мнимая части частотной ПФ. Для их нахождения необходимо избавиться от мнимости в знаменателе, умножением на сопряженную знаменателю комплексную величину. Логарифмические ЧХ - ЛАЧХ & ЛФЧХ Построение ЛАЧХ & ЛФЧХ производится по выражениям: L(w) = lg |W(jw)| = lg A(w), [лог]; j(w) = arg(W(jw)), [рад].
2. Математич. описание идеальных звеньев. (2 стр. 2-3)
Безынерционное звено
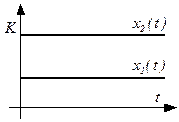
| x2( t) = Kx1( t), в операторной форме X2( p) = KX1( p) | |
|
| Передаточная функция 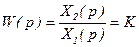 .
Комплексный коэффициент передачи .
Комплексный коэффициент передачи 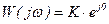 , то есть , то есть 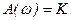 , , 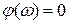 .
В логарифмическом масштабе .
В логарифмическом масштабе 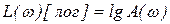
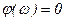 .
ЛАЧХ безинерционного звена представляет собой прямую, параллельную оси абсцисс и отстоящую от неё на расстоянии .
ЛАЧХ безинерционного звена представляет собой прямую, параллельную оси абсцисс и отстоящую от неё на расстоянии 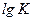 . ЛФЧХ совпадает с осью абсцисс. . ЛФЧХ совпадает с осью абсцисс.
| |
Интегрирующее звено
Идеальным интегрирующим звеном называется звено, выходная величина которого пропорциональна интегралу входной величины.
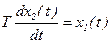 ;
; 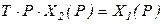 ,
,
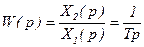
|
| ||
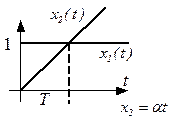
|
при при при | ||
|
| То есть в логарифмическом масштабе ЛАЧХ – прямая линия. ЛАЧХ интегрирующего звена представляет собой прямую проходящую с наклоном ЛФЧХ представляет собой прямую, параллельную оси абсцисс и отстоящую от неё на | ||
Дифференцирующее звено
Идеальным дифференцирующим звеном называется звено, выходная величина которого пропорциональна скорости изменения входной величины.
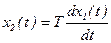 ;
; 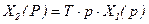 ;
;
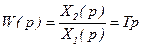 .
.

|
| |
|
| при 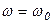 , , 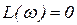 ;
при ;
при 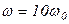 , , 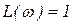 ;
при ;
при 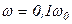 , , 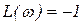 . .
| |
3. Математич. описание реальных звеньев 1 порядка. (5 стр. 3-8)
Реальные динамические звенья представляют собой соединения из элементарных звеньев.
Инерционное (апериодическое) звено 1 – го порядка
Инерционным (апериодическим) звеном 1 – го порядка называется такое звено, связь между выходом и входом определяется линейным заданным уравнением 1 – го порядка вида:
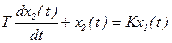 , где Т – постоянная времени инерционного звена. ( 1 )
, где Т – постоянная времени инерционного звена. ( 1 )
При ступенчатом изменении входного сигнала 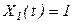 и при пул. Начальных условиях
и при пул. Начальных условиях 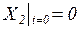 решение уравнения ( 1 ) может быть представлено в виде:
решение уравнения ( 1 ) может быть представлено в виде:
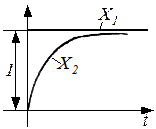
| 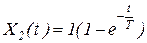
|
В операторной форме
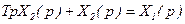
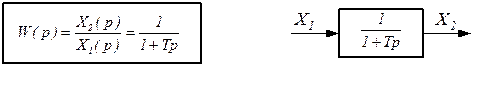
|
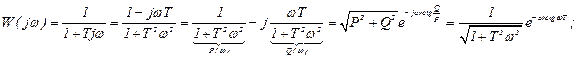
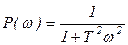 , ,
, , 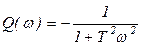 ,
, 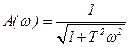
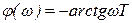 .
.
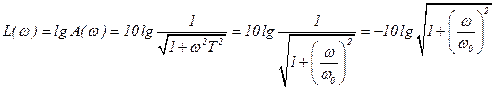 ;
;
при 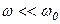
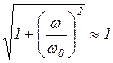 .
. 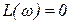 ,
, 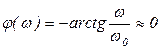 ;
;
при 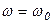
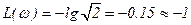 ,
, 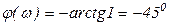 ;
;
при 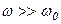
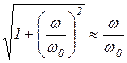
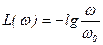 - прямая с наклоном
- прямая с наклоном 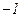 ;
;
при 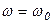
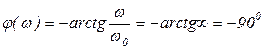 .
.
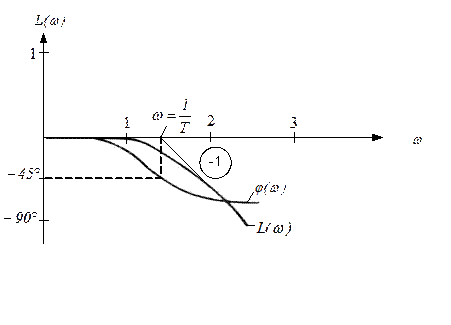
|
Реальное дифференцирующее звено 1 – го порядка
Это звено, у которого связь между выходной и входной величиной определяется уравнением вида:
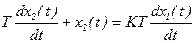 ,
,
где Т – постоянная времени звена
K – коэффициент усиления звена
Рассмотрим переходный процесс в таком звене при 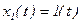 и
и 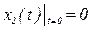
При этих условиях решение может быть записано в виде
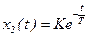 , то есть при ступенчатом изменении входного сигнала выходная величина изменяется по экспоненциальной кривой.
, то есть при ступенчатом изменении входного сигнала выходная величина изменяется по экспоненциальной кривой.
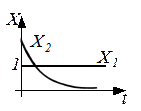
Реальные дифференцирующие звенья применяются как средство корректирования переходных процессов, например, стабилизирующий трансформатор, дифференцирующие мостовые схемы и другое.
В операционной форме 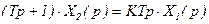 ;
; 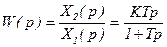
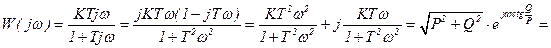
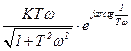
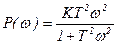 ,
, 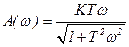 ,
,
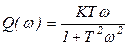 ,
, 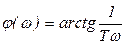 .
.
при 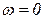 ,
, 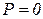 ,
, 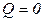 ,
, 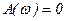 ,
, 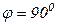
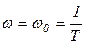 ,
, 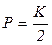 ,
, 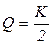 ,
, 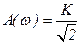 ,
, 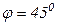
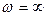 ,
, 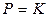 ,
, 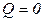 ,
, 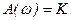 ,
, 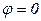
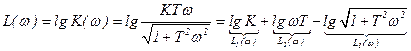
Таким образом ЛАЧХ представлена в виде 3-х составляющих:
1-я – представляет собой прямую, параллельную оси абсцисс и проходящую на уровне 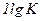
2-я – прямая, имеющая наклон 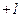 и пересекающая ось абсцисс при
и пересекающая ось абсцисс при 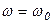 .
.
3-я – представляется двумя асимптотами, сопрягающимися при 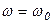 причём до
причём до 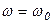 асимптоты совпадают с осью абсцисс, а после имеют отрицательный наклон
асимптоты совпадают с осью абсцисс, а после имеют отрицательный наклон 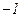 .
.
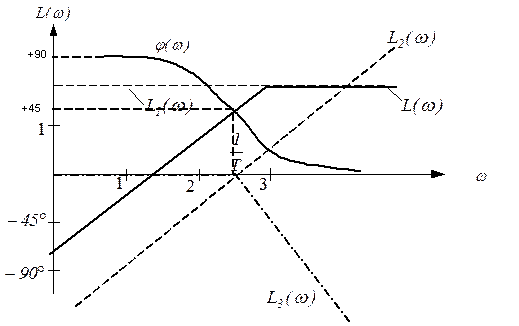
|
Реальное форсирующее звено 1 – го порядка
Это звено, у которого связь между выходом и входом выражается уравнением вида:
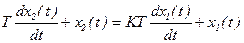
при 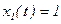 и
и 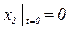
Решение может быть представлено в виде 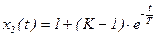
при 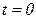
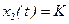
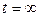
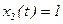
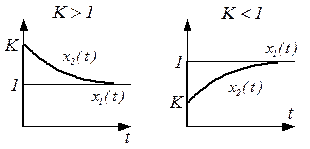
|
Реальное форсирующее звено наряду с реальным дифференцирующим звеном применяется как средство для корректирования, улучшения переходных процессов.
В операторной форме: 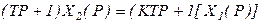
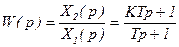
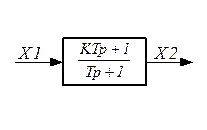
|
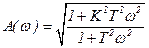 ,
,
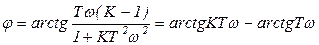
при 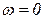 ,
, 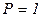 ,
, 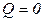 ,
, 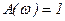 ,
, 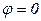
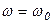 ,
, 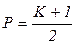 ,
, 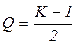 ,
, 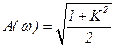 ,
, 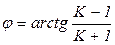
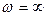 ,
, 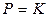 ,
, 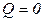 ,
, 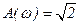 ,
, 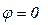
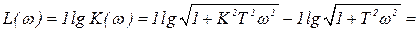
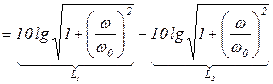
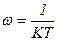 ,
, 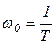
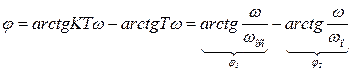
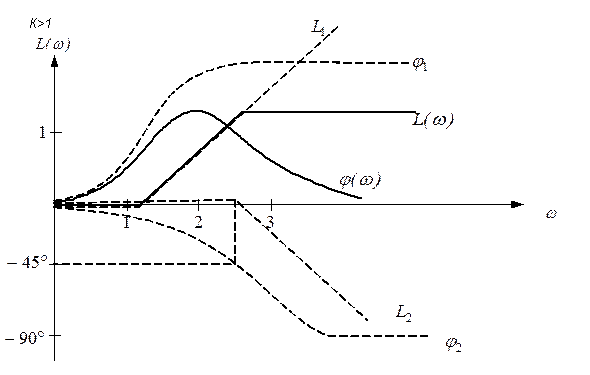
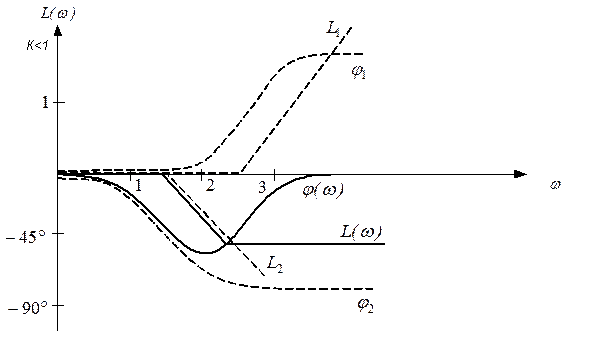
|
5.Передаточные ф-ции и ЧХ при различных соединениях звеньев. (3 стр. 12-14)
Последовательное соединение звеньев
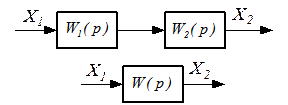
| Дано: W 1 (р), W 2 (р),
L 1 ( ω ), L 2 ( ω ),
φ1(ω), φ2(ω)
 L (ω) = ? φ(ω) = ?
L (ω) = ? φ(ω) = ?
|
Известно, что W ( р) = W 1 (р)· W 2 (р) переходя к АФЧХ, p = j ω :
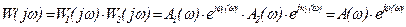 ,
,
A( ω ) = A 1 (ω)·A2(ω), φ ( ω ) = φ1(ω) + φ2(ω),
переходя к логарифмическому масштабу
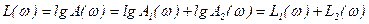 .
.
таким образом 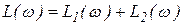 ,
,
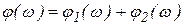 .
.
| Рассмотрим пример: | 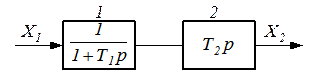
|
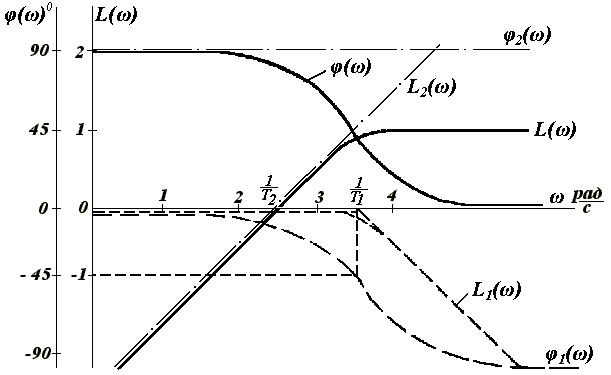
Согласно-параллельное соединение звеньев
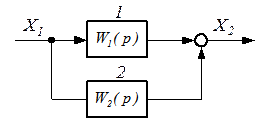
| Дано: W 1 (р), W 2 (р),
L 1 ( ω ), L 2 ( ω ),
φ1(ω), φ2(ω)
 L(ω) = ? φ(ω) = ?
L(ω) = ? φ(ω) = ?
|
W (р) = W 1 (р) + W 2 (р), (1)
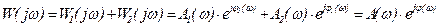 . (2)
. (2)
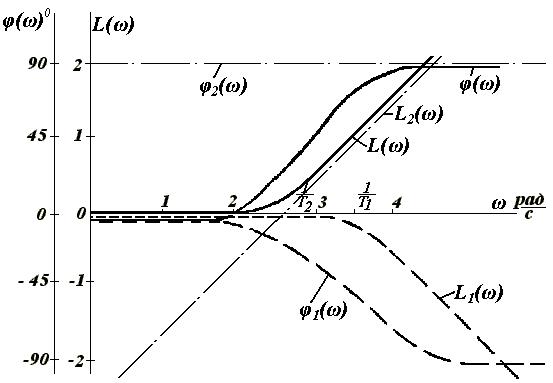
Bскомые ЛАЧХ и ФЧХ находятся путем добавления поправочных ординат к характеристикам 2-го звена, т.е., опять-таки, к характеристикам звена ЛАЧХ, которое идет выше.
При малых L П, φП искомые характеристики будут, очевидно, совпадать с характеристиками того звена ЛАЧХ, которое проходит выше.









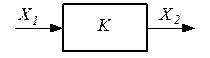
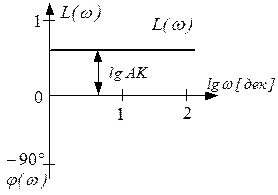
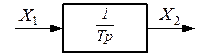
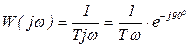 ;
; 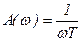 ;
; 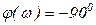 .
.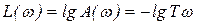 ,
,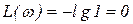 ,
,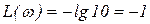 ,
,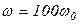
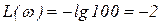 ,
,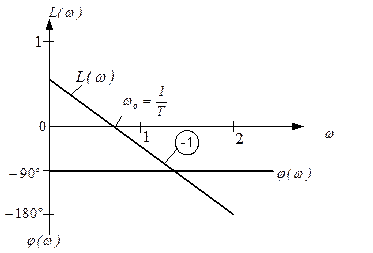
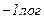 и пересекающую ось абсцисс при частоте, равной обратной величине постоянной времени звена.
и пересекающую ось абсцисс при частоте, равной обратной величине постоянной времени звена.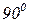 .
.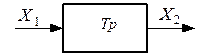
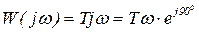 ;
;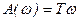 ;
;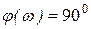 ;
;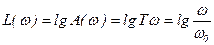 .
.