Тема 4. Решение показательных неравенств
Теорема:
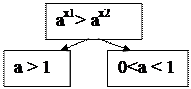 |
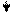
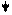
|
|
Задание1: Заполнить таблицу:
| № | Неравенство | Основание степени | Изменение знака |
| 1 | 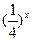 > > 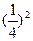
| 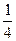
| Т.к. 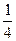 < 1, то знак меняем < 1, то знак меняем
|
| 2 |  4х<16 4х<16
| 4 | Т.к 4>1, то знак сохраняем |
| 3 | 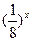 > > 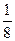
| ||
| 4 | 5х+1>125 | 5 |
Пример: Решить показательное неравенство:
23х-5>16
Решение:
23х-5>24, т.к. 2>1, то знак сохраняем
3х-5>4
3х>4+5
3х>9
х> 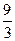
х>3, Ответ: х>3
Задание 2: Из предложенных ниже ответов, найти тот, который является решением неравенства:
а) 2х>32 в) ( 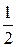 )х >32
)х >32
1) х>5 2) x=5 3) x<5
Задание 3: Найти пример, решение которого неверно:
1) 3х >81 2) 3х > 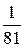 3) (
3) ( 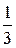 )х >
)х > 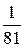
Решение: Решение: Решение:
3х>34, т.к. 3>1, то знак сохраняем 3х>3-4, т.к. –4<0, то знак меняем ( 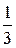 ) х>(
) х>( 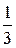 )4, т.к.
)4, т.к. 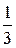 <1, то знак меняем
<1, то знак меняем
х>4 х<-4 х<4
Ответ: х>4 Ответ: х<-4 Ответ: х<4
Задание 4: Решить самостоятельно показательное неравенство:
1) 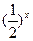 >
> 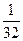 3) 4х<
3) 4х< 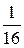
|
|
 2) 62х-4<216 4) (
2) 62х-4<216 4) ( 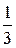 )х+1 >
)х+1 > 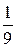
| ||||
| ||||
Пример: Решить показательное неравенство:
3х+2+3х-1<28
Решение:
3х·32+ 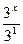 <28
<28
Пусть 3х=t,t>0 t< 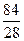
t·32+ 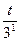 <28 t<3
<28 t<3
9t+ 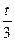 <28 3х<3
<28 3х<3
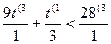 3х<31, т.к.3>1, то знак сохраняем
3х<31, т.к.3>1, то знак сохраняем
27t+t<84 х<1
28t<84 Ответ: х<1
Задание 5: Решить показательное неравенство:
1)3х+1-2·3х-1-4·3х-2 <17 3) 5х-7·5х-2<90
2) 5х+3·5х-1+2·5х-2>42 4) 2х+4-2х>120

Проверь себя!
| Решить показательное неравенство: |
1. 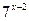 >49 >49
|
2. 5х-1≤ 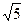
|
3. 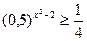
|
4. 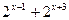 >17 >17
|
5. 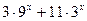 <4 <4
|
Контрольная работа
Уровень А: 1) Упростить
а) 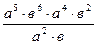
б) 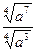
2) Решить показательное уравнение
а) 2х=8
б) 2х+1 + 3·2х-1 -5·2х = -6
в)4х-6·2х+8=0
г) 3·9х-10·3х+3=0
3) Решить показательное неравенство
а) 5х<625
б) 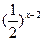 >
> 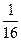
в) 2х+2-2х>96
Уровень В: 1) Упростить
а) 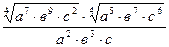
б) 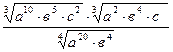
2) Решить показательное уравнение
а) 2х+2х-3=18
б) 2х+1 + 2х-1 +2х = 28
в) 4х+1-5·2х +1=0
3) Решить показательное неравенство
а) 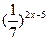 >
> 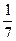
б) 3х-2·3х-2>7
Уровень С: 1) Упростить
а) 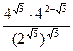
2) Решить показательное уравнение
а) 7х+2+3·7х-1=346
б)5х-2 + 5х-3 +5х-4 = 155
в) 9х+3х+4-810=0
г) 22х+1-5·2х+2=0
3) Решить показательное неравенство
а) 2х-2 + 2х-1 +2х <4
б) 4х-3·2х+2>0
Подготовка к Единому Государственному экзамену (ЕГЭ)
|
|

Тренировочная работа №1








