Тема 3. Решение показательных уравнений
Определение: Показательным уравнением называется уравнение, в котором неизвестное содержится в показателе степени.
Задание 1: Выбрать показательное уравнение:
1) 4х=64 3) 644=х
2) 4х=64 4) х4=64
Теорема:Если ах=ав, где а>0, а≠1, то х = в
Задание 2: Пользуясь теоремой, заполнить таблицу:
| № | Показательное уравнение | ответ |
| 1 | 2х=23 | х=3 |
| 2 | 5х=56 | х=…. |
| 3 | 4х=42 | х=…. |
| 4 | 9х=81 (9х=92) | х=2 |
| 5 | 7х=243 | х=…. |
| 6 | 2х=32 | х=…. |
| 7 | 6х= 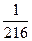
| х=…. |
Пример: Решить показательное уравнение:
1) 43х+15=1 2) 52х-7= 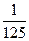
Решение: Решение:
43х+15=40 52х-7=5-3
3х+15=0 2х-7=-3
3х=0-15 2х=-3+7
3х=-15 2х=4
х= 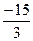 х=
х= 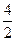
х=-5 х=2
Ответ: х=-5 Ответ: х=2
Задание 3: Решить самостоятельно и выбрать правильный ответ:
1) 62х+5=216
2) 3х-4= 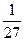
3) 74х=1
 а) х=-1 б) х=0 в) х=1
а) х=-1 б) х=0 в) х=1
Задание 4: «Иди по стрелке»
|
|
|
|
|
|
|
|
|


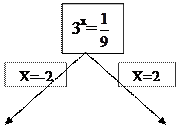 | |||
 | |||
(Раздели полученный результат на 2 и получи оценку
Задание 5: Пользуясь свойствами, заполнить таблицу:
| № | пример | Используемое свойство | результат |
| 1 | 6х-2 | 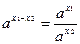
| 6х-2= 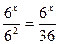
|
| 2 | 4х+1 | 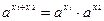
| |
| 3 | (32)х | ||
| 4 | 5х+4 | ||
| 5 | 23х | 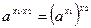
| 23х=(23)х=8х |
| 6 | 9х·92 | 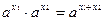
| |
| 7 | 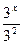
|
Пример: Решить показательное уравнение:
3х+2+3х=90
Решение:
3х·32+3х=90 t=9
Пусть 3х=t,t>0 3х=9
t·32+t=90 3х=32
9t+t=90 х=2
10t=90 Ответ: х=2
t= 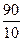
t=9
Задание 6: Найти ошибку в решении показательного уравнения:
3х+2-5·3х=36
Решение:
3х·32-5·3х=36 t=9
Пусть 3х=t,t>0 3х=9
t·32-5·t=36 3х=33
9t-5·t=36 х=3
4t=36 Ответ: х=3
t= 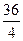 , t=9
, t=9
Задание 7: Заполнить таблицу:
| № | уравнение | Расписать по формуле | t=…. | Найти t | х=…. |
| 1 | 3х+2+3х=90 | t·32+t=90 | 3х=t | t·32+t=90
9t+t=90 10t=90 t= 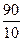 t=9
t=9
| t=9 3х=9 3х=32 х=2 Ответ: х=2 |
| 2 | 2·5х+2-10·5х=8 | 2·5х·52-10·5х=8 | 5х=t | 2·t·52-10·t=8 2·t·25-10·t=8 50t-10t=8 ……. | |
| 3 | 4х+1+4х=320 | 
| |||
| 4 | 3х+4·3х+1=13 | ||||
| 5 | 7х+2-14·7х=5 |
Пример: Решить показательное уравнение:
2х-1+2х=6
Решение:
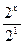 +2х=6
+2х=6
Пусть 2х=t,t>0 t= 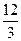
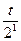 +t=6 t=4
+t=6 t=4
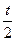 +t=6 2х=4
+t=6 2х=4
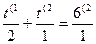 2х=22
2х=22
1t+2t=12 х=2
3t=12 Ответ: х=2
Задание 8: Дорешать самостоятельно:
1) 3х-3+3х-1=10
Решение:
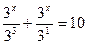
Пусть 3х=t,t>0
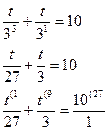
10t+9t=270, 10t=270, t= 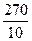 , t=27, 3х=27, 3х=33, х=….., Ответ: х=……
, t=27, 3х=27, 3х=33, х=….., Ответ: х=……
2) 53х+3·53х-2=140
Решение:
53х+3· 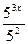 =140
=140
Пусть 53х=t,t>0
t+ 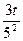 =140
=140
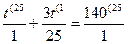
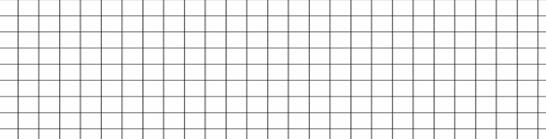
Ответ: х=……..
Задание 9: Решить показательное уравнение:
1) 2х+2х-3=18
2) 8·2х-1-2х=48

Пример: Решить показательное уравнение:
3х+1-4·3х-2=69
Решение:
3х·31-4· 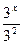 =69
=69
Пусть 3х=t,t>0 t= 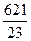
t·31-4· 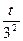 =69 t=27
=69 t=27
3t- 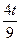 =69 3х=27
=69 3х=27
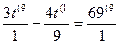 3х=33
3х=33
27t-4t=621 х=3
23t=621 Ответ: х=3
Задание 10: Проанализировать решение и найти ошибку:
2х+1 + 2х-1 +2х = 28
Решение:
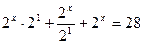
Пусть 2х =t, t > 0
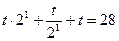 t=
t= 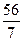
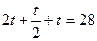 t=8
t=8
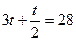 2х =8
2х =8
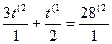 2х =24
2х =24
6t+t=56 х = 4
7t=56 Ответ: х = 4
Задание 11: Решить показательное уравнение:
1) 10·5х-1 +5х+1 = 7
2)7х+2 +4·7х-1 = 347 Ответ записать в виде таблицы:
3) 4·3х-1 +3х+1 = 117
| Ответ | х =0 | х =1 | х =2 |
| № уравнения |

Пример: Решить показательное уравнение:
9х +8·3х –9 = 0
Решение:
(32)х+8·3х –9 = 0
(3х)2+8·3х –9 = 0
Пусть 3х =t, t > 0
t2 +8· t –9 =0
а=1, b=8, с=-9
t1,2= 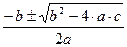 =
= 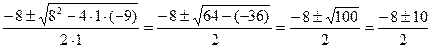
t1= 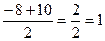 t2=
t2= 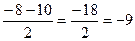
t1= 1 t2= -9, не уд., так как t>0
3х = 1
3х =30
х=0
Ответ: х=0
Задание 12: Проверить решение, удалить посторонний корень и записать ответ: 4х –2х –12 = 0
Решение:
(22)х–2х –12 = 0
(2х)2–2х –12 = 0
Пусть 2х =t, t > 0
t2 – t –12 =0
а=1, b=-1, с=-12
t1,2= 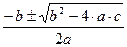 =
= 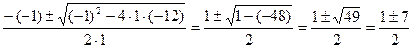
х1= 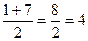 х2=
х2= 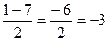
t1= 4 t2= -3
2х = 4 ……..
2х = ….. Ответ: х=……
Задание 13: Решить показательное уравнение и стрелками сопоставить правильный ответ:
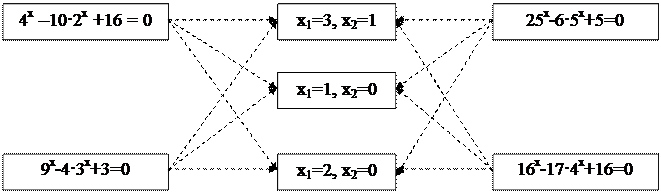
Проверь себя!
| Решить показательное уравнение: |
1. 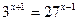
|
2. 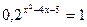
|
| 3. 4·3х+2+5·3х+1-6·3х =5 |
4. 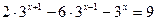
|
5. 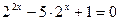
|








