Тема 2. Показательная функция, её свойства и график
Историческая справка
В письмах немецкого философа, физика – изобретателя и математика Г.Лейбница (1646-1716) к голландскому учёному Х.Гюйгенсу (1629-1695), датированных 1679г., можно найти использование (без пояснений) переменной величины в показателе степени.
Начиная IIX века европейские математики, ещё не имея строгой теории действительных чисел, изучали отдельные свойства показательной функции. В IX веке после того как в математики упрочилось понятие предела и было введено понятие степени с действительным показателем, удалось строго обосновать и свойство показательной функции.
В биологии есть законы, которые можно описать с помощью показательной функции. Например:
1. Закон органического размножения: при благоприятных условиях (отсутствие врагов, большое количество пищи) живые организмы размножались бы по закону показательной функции.По такому же принципу распространились завезённые в Австралию кролики, которые стали экологической катастрофой для этого уникального региона. Рост различных видов микроорганизмов и бактерий, дрожжей, ферментов все эти процессы подчиняются одному закону: N = N0ekt
Ещё по этому закону возрастает количество клеток гемоглобина в организме человека, который потерял много крови.
2. Закон органического затухания: подобен размножению, происходит с той же скоростью и по тем же условиям, но происходит в обратную сторону.
3. Закон выравнивания: он тоже описывается показательной функцией и присутствует при таких процессах, как разрушение адреналина в крови и уменьшение количества радиоактивных веществ, выводимых почками.
Эти законы доказывают нам, что показательная функция имеет большое практическое значение в биологии, а особенно в таких её разделах, как экология и медицина.
В физике тоже есть величины и законы подчиненые показательной функции:
1. Например процесс изменения температуры чайника при кипении выражается формулой: T = T0+ (100 - T0)e-kt - это пример процесса выравнивания, который в физике также можно наблюдать при включении и выключении электрических цепей, и при падении тела с парашютом.
2. Также широко применяется показательная функция при описании процессов ядерной физики:
Когда радиоактивное вещество распадается, его количество уменьшается, через некоторое время остается половина от первоначального вещества. Этот промежуток времени t0 называется периодом полураспада. Общая формула для этого процесса: m = m0(1/2)-t/t0 , где m0 - первоначальная масса вещества. Чем больше период полураспада, тем медленнее распадается вещество. Это явление используют для определения возраста археологических находок. Радий, например распадается по закону: M = M0e-kt, используя данную формулу ученые рассчитали возраст Земли (радий распадается нормально за время равное возрасту Земли).
3. В ядерных реакциях: скорость разветвлённо-цепного процесса в
газовой фазе в начальных стадиях (вплоть до выгорания 30-40% газа) выражается формулой: 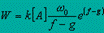 , где k - константа скорости реакции активного центра с исходным веществом, [А] - концентрация исходного вещества, w0 - скорость зарождения цепей, f и g - соответственно эффективные константы скорости разветвления и обрыва, e - основание натурального логарифма, t - время.
, где k - константа скорости реакции активного центра с исходным веществом, [А] - концентрация исходного вещества, w0 - скорость зарождения цепей, f и g - соответственно эффективные константы скорости разветвления и обрыва, e - основание натурального логарифма, t - время.
4. При прохождении света через мутную среду каждый слой этой среды
поглощает строго определенную часть падающего на него света. Сила
света I определяется по формуле: I = I0e-ks , где s – толщина слоя,
k – коэффициент характеризующий мутную среду.
Показательная функция, её свойства и график
Определение: Функцию у=ах, где а>0, а≠1, называют показательной функцией.
Свойство 1: Область определения показательной функции у=ах – множество R всех действительных чисел.
Свойство 2: Множество значений показательной функции у=ах – множество положительных чисел.
Свойство 3: Показательная функция у=ах является возрастающей, если а>1, и убывающей, если 0<а<1.
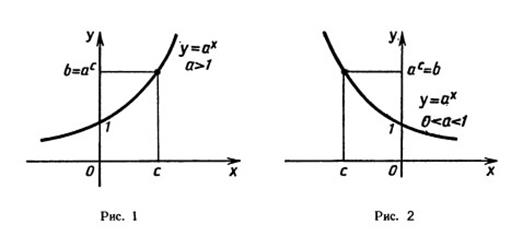
Пример: Построить графики функции у=2х, у=( 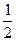 )х
)х
Составим таблицы:
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| у=2х | 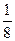
| 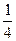
| 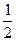
| 1 | 2 | 4 | 8 |
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
у=( 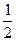 )х )х
| 8 | 4 | 2 | 1 | 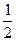
| 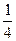
| 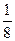
|
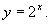
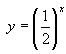
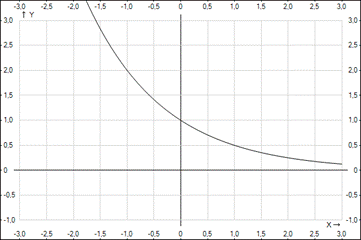
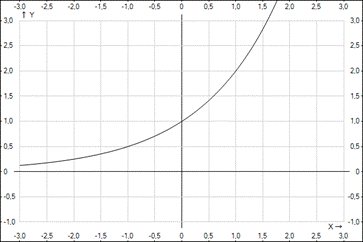 Схематично построим графики:
Схематично построим графики:
Задание 1: Построить графики функции у=3х, у=( 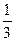 )х
)х
|

|

Проверь себя!
| Решить графически уравнение: (построив графики функций левой и правой части уравнения на одном чертеже и определив точку их пересечения) |
1. 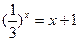
|
2. 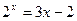
|








