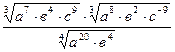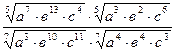Тема 1. Степень с действительным показателем
Сборник упражнений
по теме
«Показательная функция»
Дисциплина: Математика
Введение
Данная рабочая тетрадь может использоваться как самостоятельно (так как в тетрадь включены не только множество заданий разной степени сложности, но и все необходимые определения, подробные примеры и пояснения к ним), так и совместно с учебниками:
§ «Алгебра и начала анализа 10-11 класс» Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Шабунин М.И., М:Просвещение;
§ «Алгебра и начала анализа 10класс» Колягин Ю.М., Сидоров Ю.В., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И., М:Мнемозина;
В данной рабочей тетради использованы различные формы изложения материала. Для изучения нового материала рабочие тетради оформлены как полноценный конспект, в котором есть и теория, и примеры решённых заданий, и задания для самостоятельного выполнения. Учебные пособия - рабочие тетради, разработаны так, что по алгоритму и количественной части решённого, а также с учетом возрастания сложности необходимо выполнить задание. При выполнении данных заданий требуются умения систематизировать, сравнивать, анализировать предложенную информацию, применять имеющиеся знания и умения в нестандартной ситуации. Причём информация представлена в различных видах (схемы, таблицы и тд.). Задание так же имеют разную формулировку и различны по своему характеру: вводные, пробные, по образцу, творческие. Помимо упражнений и заданий в тетради включены и справочные материалы. В конце тетради предлагается уровневая контрольная работа, но выполнять её можно частями (при окончании изучения тем «Степень с действительным показателем», «Решение показательных уравнений» и «Решение показательных неравенств», чтобы легче контролировать усвоение материала и корректировать ошибки).
Использование рабочей тетради в учебном процессе позволяет осуществить: во-первых, достижение уровня обязательной математической подготовки; во-вторых сформировать умение применять полученные знания в несколько отличных от обязательных результатов обучения ситуациях; в – третьих ведёт к повышению активности и самостоятельности, планированию собственной деятельности.
Содержание учебного материала
| Раздел Показательная функция | |
| Тема 1 Степень с действительным и рациональным показателем. | Степень с действительным и рациональным показателем. Арифметический корень натуральной степени. |
| Тема 2 Показательная функция, ее свойства и график | Определение и график показательной функции, три основных свойства показательной функции |
| Тема 3 Показательные уравнения | Определение и вид показательных уравнений, алгоритм решения показательных уравнений. |
| Тема 4 Показательные неравенства | Определение и вид показательных неравенств, алгоритм решения показательных неравенств. |
Тема 1. Степень с действительным показателем
Историческая справка
Ещё в V веке до н.э. в школе Пифагора было доказано, что множество рациональных чисел не хватает для точного измерения длин любых отрезков. Одной из первых задач, выводящих на понятие несоизмеримости отрезков, была задача нахождения стороны квадрата, площадь которого равна 2. Тем самым было доказано существование несоизмеримых отрезков. Идею доказательства методом от противного факта несоизмеримости диагоналей квадрата и его сторон можно найти в «Началах» Евклида (IV век до н.э.).
Все последующие после Евклида годы, вплоть до XII в., математики Индии и Востока использовали иррациональные величины для нужд математической науки и астрономии, но не признавали их за числа. В начале XIIв. Персидский и таджикский поэт, математик и философ Омар Хайям (ок.1048 – после 1112) теоретически расширил понятие числа до положительного действительного числа. ВXV в. Самаркандский учёный аль-Каши стал применять десятичные дроби для увеличения точности извлечения корней. В 1594г. Нидерландский математик и инженер Симон Стевин (1548-1620) в книге «Приближение к алгебре» показал, что десятичные дроби можно использовать для бесконечного приближения к точному значению иррационального числа. Позже французский математик, философ, физик и физиолог Рене Декарт (1596 – 1650) показал, то иррациональные числа, как и рациональные, изображаются точками на числовой оси и образуют вместе с рациональными числами множество действительных чисел.
Степень с действительным показателем
Определение:
 ах = а · а · а · ··· · а , где ах –степень,
ах = а · а · а · ··· · а , где ах –степень,
а – основание степени
х раз n – показатель степени
Таблица степеней:
| степень | -2 | -1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| число | ||||||||||||
| 2 | 1/4 | 1/2 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 | 1/9 | 1/3 | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | |||
| 4 | 1/16 | 1/4 | 4 | 16 | 64 | 256 | 512 | 1024 | ||||
| 5 | 1/25 | 1/5 | 5 | 25 | 125 | 625 | 3125 | |||||
| 6 | 1/36 | 1/6 | 6 | 36 | 216 | 1296 | ||||||
| 7 | 1/49 | 1/7 | 7 | 49 | 343 | |||||||
| 8 | 1/64 | 1/8 | 8 | 64 | 512 | |||||||
| 9 | 1/81 | 1/9 | 9 | 81 | 729 |
Задание 1: Вычислить по примеру:
35= 3·3·3·3·3=243
54=……………..
28=……………..
42=…………….
Задание 2: Заполнить, так чтобы равенство было верным:
2….=8
3….=81
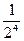 =2-….
=2-….
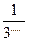 =3-5
=3-5
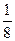 =2….
=2….
Основные свойства степени:
1) а0 = 1 , а ≠ 0
2) а-n = 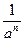 , а ≠ 0
, а ≠ 0
3) 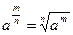
4) 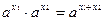
5) 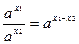
6) 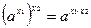
7) 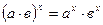
8) 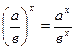
Задание 3: Записать в виде степени результат выполнения действий, заполняя пропуски:
1) 59 : 52 · 5-4 = 59-2+(-4)=53
2) 7-2 · 73:78=7-2+………=7…
3) 212:2-5·2-7=212- ………=2…
4) (43)-2·43=4………=4…….
5) (7-6)-3:7-7=7………=7…
Задание 4: Заполнить таблицу, используя равенство 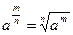 , где х>0
, где х>0
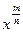
| 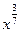
| 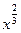
| 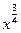
| |
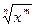
| 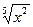
| 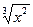
|
Пример: Упростить:
1) 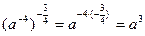
2) 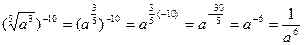
3) 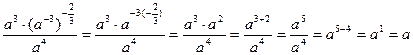
Задание 5:Упростить:
1) 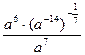 5)
5) 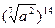
2) 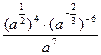 6)
6) 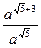 Ответ записать в виде таблицы:
Ответ записать в виде таблицы:
| Ответ | 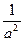
| 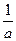
| 1 | а | а2 | а3 | а4 |
| №задания |
3) 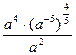 7)
7) 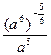
 4)
4) 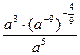
Пример: Упростить:
1) 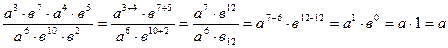 2)
2) 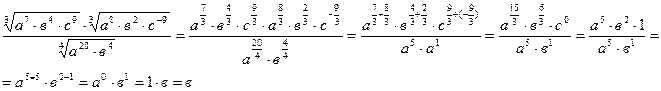 Задание 6: Соединить пример с правильным ответом:
Задание 6: Соединить пример с правильным ответом:
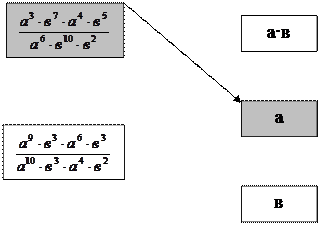 |
| |||
| ||||

Задание 7: Выполнить устно тест, выбирая букву с правильным ответом:
1) 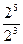
У: 4 Б: 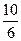
2) 1610·16-9
Б: 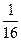 М: 16
М: 16
3) 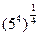
О: 125 Н: 5
4) 60
И: 1 М: 0
5) 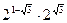
Ц: 2 И: 2
6) (3·2)2
Н: 3·22=3·4=12 А: 32·22=9·4=36
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| Ответ(буква) |
Проверь себя!
| 1. Вычислить | 2. Упростить выражение: |
1) 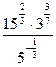
| 1) 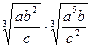
|
2) 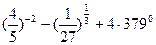
| 2) 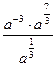
|
3) 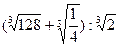
| 3) 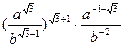
|
4) 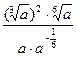
| 4) 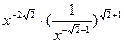
|