II. Решение задач.
9 класс Алгебра 19.10.2022
Тема: Решение текстовых задач алгебраическим методом
Цели урока.
Образовательные:
систематизировать знания и умения учащихся решать текстовые задачи.
Развивающие:
совершенствование, развитие, углубление знаний, умений, навыков по решения текстовых задач;
развитие мыслительной деятельности: умение анализировать, обобщать, сравнивать;
развитие творческой деятельности: смекалки;
развитие математической речи и графической культуры, памяти
Воспитательные:
формирование мировоззрения с помощью взаимосвязанной системы знаний по данной теме;
формирование обще учебных навыков: вычислительных, эстетических навыков при оформлении записей;
формирование качеств личности: трудолюбия, самостоятельности, стремления к самореализации.
Ход урока
I. Устный счёт
Фронтальная работа.
Найдите 30% от 27. (0,9)
Какое число получится, если 140 увеличить на 60%? (224)
Кафельная плитка продается коробками по 6 м2. Сколько коробок плитки нужно купить, чтобы хватило на облицовку стен площадью 35 м2? (6)
Билеты в ботанический сад стоит 50 рублей. Сколько рублей сдачи нужно получить с 2000 рублей, заплаченных за проход 36 человек? (200)
Горные лыжи стоят 16 000 рублей. Сколько рублей будут стоить горные лыжи во время сезонной распродажи, когда на них объявлена скидка 20%? (12800)
II. Решение задач.
1. Задачи на движение (оформите решение задач в тетради)
В настоящее время на экзамене по математике в блоке “алгебра” предлагаются задачи, решение которых требует составления уравнения, а также их систем на основании условия задачи.
Указания к задачам:
1.Основными компонентами этого типа являются:
а) пройденный путь (S);
б) скорость (v);
в) время (t).
2. Зависимость между величинами выражается известными формулами:
S=v/t; v=S/t; t=S/v.(Указанные величины должны быть в одной системе единиц, например: путь в км, время в часах, то скорость в км/час.)
Задача 1. Пристани А и В расположены на реке, скорость течения которой на этом участке равна 4 км/ч. Лодка проходит от А до В и обратно без остановок со средней скоростью 6 км/ч. Найти собственную скорость лодки.
Решение:
Пусть х км/ч – собственная скорость лодки.
| Лодка | V км/ч | tчас | Sкм |
| Из А в В | x-4 | S/x-4 | S |
| Из В в А | X+4 | S/x+4 | S |
Составим уравнение:
(S/x-4 + S/x+4)*6=2 S.
 Решите уравнение самостоятельно
Решите уравнение самостоятельно
Получим х=8 км/ч или х=-2(не удовлетворяет условию задачи)
Ответ: 8 км/час.
2. Задачи на совместную работу.
Алгоритм решения задач на совместную работу
Принимаем всю работу, которую необходимо выполнить за 1.
Находим производительность труда каждого рабочего в отдельности, т.е., где t – время, за которое этот рабочий может выполнить всю работу, работая отдельно.
Находим ту часть всей работы, которую выполняет каждый рабочий отдельно за то время, которое он работал.
Составляем уравнение, приравнивая объем всей работы к сумме слагаемых, каждое из которых есть часть всей работы, выполненная отдельно каждым из рабочих.
Задача 2. Две трубы, работая вместе, наполнили бассейн за 12 часов. Первая труба, работая отдельно, наполняет бассейн на 18 часов быстрее, чем вторая. За сколько часов наполняет бассейн вторая труба.
Решение:
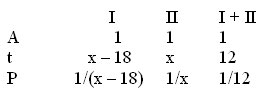
1/12 = 1/(x – 18) + 1/x
Х2 -42Х +216=0
Х1=36; Х2 =6 (не удовлетворяет условию задачи)
Ответ: 36 часов.
3. Задачи с использованием формул двузначного числа
Алгоритм решения задач, в которых используется формула двузначного числа.
Вводится обозначение:
х – цифра десятков
у – цифра единиц
Искомое двузначное число 10х + у
Составить систему уравнений.
Задача 3. Двузначное число в четыре раза больше суммы его цифр. Если к этому числу прибавить произведение его цифр, то получится 32. Найдите это двузначное число.
Х – цифра десятков. У – цифра единиц. 10х + у – искомое число.
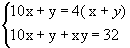
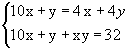
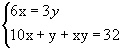
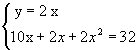
2х2 + 12х – 32 =0
х2 +6х – 16 =0
х1 =-8 (посторонний корень)
х2 =2, тогда у =4.
Ответ: 24.
4. Задачи на смеси и растворы.
Алгоритм решения задач на смеси.
х – масса первого раствора, у – масса второго раствора, (х + у) – масса полученной смеси.
Найти содержание растворенного вещества в растворах, т.е.
а % от х, в % от у, с % от (х+у)
Составить систему уравнений.
Задача 4. Смешали 30%-й раствор соляной кислоты с 10%-м и получили 600 г 15%-го раствора. Сколько граммов каждого раствора было взято?
Решение:
Введем обозначение. Пусть взяли х г первого раствора, у г – второго раствора, тогда масса третьего раствора – (х+у).
Определим количество растворенного вещества в первом, втором, третьем растворах, т.е. найдем 30% от х, 10% от у, 15% от 600.
15% от 600=90
Составим систему уравнений:
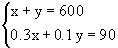
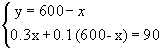
0,3х + 60 – 0,1х = 90
0,2х = 30
х = 30:0,2
х = 150, у = 600 – 150 = 450
Ответ: взяли 150 г первого раствора и 450 г второго раствора.
III. Подведение итогов урока (4 минуты)
Ребята вы сегодня от души потрудились, порадовали меня своими знаниями. У кого 4 и более жетончиков подойдите с дневниками. Проставляю оценки в журнал:
4-5 ж - “4”,
5 и более жетонов - “5”.
IV. Домашнее задание. Решите задачу 5.
Задача 5. Две машины, работая вместе, могут расчистить каток за 20 минут. Если первая машина будет работать 25 минут, а затем её сменит вторая, то она закончит расчистку катка через 16 минут. За сколько времени может расчистить каток каждая из машин, работая отдельно?








