Тема урока: Решение текстовых задач алгебраическим методом
9 класс Алгебра 17.10.2022
Тема урока: Решение текстовых задач алгебраическим методом
Цель: формирование способности учащихся обобщать и систематизировать знания при решении задач с помощью рациональных уравнений.
Ход урока:
1. Подготовка обучающихся к восприятию учебного материала. Приветствие, ориентация класса на работу, изложение плана работы на уроке.
-Какие уравнения называются дробными рациональными?
-Алгоритм решения дробных рациональных уравнений:
| 1. Найти общий знаменатель дробей, входящих в уравнение. |
| 2. Умножить обе части уравнения на общий знаменатель. |
| 3.Решить получившееся уравнение. |
| 4. Исключить проверкой из корней уравнения те, которые обращают в нуль общий знаменатель. |
Фронтальная работа
1.Среди данных уравнений выберите то, которое не является дробным рациональным:
1)  ;
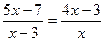2) 
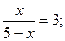3)  .
|
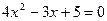2.При каких значениях переменной х уравнение 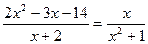 не имеет смысла:
1) -2;
2) -2 и -1;
3) всегда имеет смысл.
|
3.Сколько корней имеет уравнение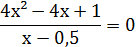 
1) 1 корень;
2) не имеет корней;
3) 2 корня.
|
4. Найти корни уравнения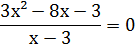 
1) х=-⅓;
2) х=⅓ или х=-3;
3) х=-⅓ или х=3.
|
| 5.Укажите общий знаменатель:
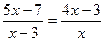1) х-3;
2) х(х-3);
3) (5х-7)(4х-3).
|
2. Запишите тему нашего урока «Решение текстовых задач алгебраическим методом».
Перед нами стоит задача: совершенствовать навык составления уравнения по условию задачи и умение проверять соответствие найденного решения условиям задачи.
Мы научились решать дробные уравнения.
А для чего они нужны? Какие задачи приводят к их появлению?
- Такие, в которых одна величина выражается через другие при помощи дробного выражения.
Например: время =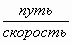 
; 
;
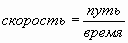Cторона прямоугольника=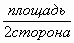 
;
;
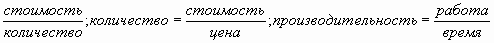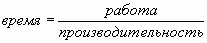и другие.
Для начала, давайте вспомним основные этапы решения задачи на составление уравнения. Нам известны три этапа. Какие это этапы?
1. Анализ условия, составление математической модели.
2. Работа с моделью.
3. Запись ответа.
5.Решение задач (оформите решение задач в тетради)
Самостоятельное решение задачи с последующей записью решения на доске.
Задача 2.Числитель дроби на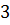 
меньше её знаменателя. Сумма дроби и обратной ей дроби в 
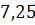раза больше исходной дроби. Найти исходную дробь.
Обозначим за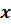 
– знаменатель дроби. Тогда 
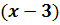– числитель этой дроби. Значит, исходная дробь имеет вид 
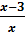. Так как по условию задачи сумма дроби 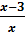и обратной ей дроби 
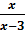в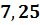 
раза больше исходной дроби, то можем составить уравнение:
Задача 3.
Две бригады, работая вместе, вспахали поле за 8 ч. За какое время может вспахать поле каждая бригада, работая самостоятельно, если второй бригаде на это необходимо на 12 ч больше, чем первой?
Решение:
Пусть x ч – время выполнения работы 1-ой бригадой.
Тогда (x +12)ч – время выполнения работы 2-ой
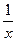бригадой,
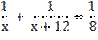
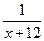- производительность 1- ой бригады,
- производительность 2-ой бригады.
Зная, что совместная производительность бригад 1/8, составим и решим уравнение:
х1=12, х2 =-8 (не удовлетворяет условию задачи)
12ч – время работы 1 бригады, (12+12)=24(ч) – время работы 2 бригады.
Ответ: 12ч, 24ч.
6. Итак, в нашем распоряжении несколько минут, поэтому давайте подведем итоги.
Вы, наверное, обратили внимание, что были решены задачи разного характера, и решение каждый раз сводилось к решению дробных рациональных уравнений.
А закончить наш урок хотелось бы словами великого ученого А.Эйнштейна: «Мне приходится делить свое время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно».
Для дальнейшего совершенствования навыка составления уравнений по условию задачи в качестве домашнего задания предлагаю вам решить следующую задачу:
Расстояние между двумя селами равно 120 км, один мотоциклист проезжает на 30 мин быстрее, чем второй. Найти скорость каждого мотоциклиста, если известно, что скорость второго на 20 км/ч меньше скорости первого.