Тема 11. Решение простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами называются неравенства вида:
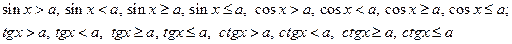
Тригонометрические неравенства могут быть решены по следующему общему правилу.
1. Найти область допустимых значений неизвестной (ОДЗ).
2. Записать соответствующее уравнение, заменив знак неравенства знаком равенства.
3. Решить уравнение, полученное в предыдущем пункте.
4. На числовой оси отметить ОДЗ, корнями уравнения разбить ОДЗ на промежутки.
5. На каждом интервале выбрать одну пробную точку и подставить ее в исходное неравенство. Если неравенство выполняется, то данный интервал необходимо включить в ответ. Если неравенство не выполняется, то интервал следует исключить из рассмотрения.
6. Сделать отбор характерных для неравенства точек – корней уравнения и концов промежутков ОДЗ. Если исходное неравенство нестрогое, то корни уравнения следует записать в ответ, в противном случае – отбросить. Концы промежутков ОДЗ проверить подстановкой в исходное неравенство. Подходящие из них включить в ответ.
Решение неравенств с синусами
| Неравенства вида sin t < a | |
| 0<a<1 | -1<a<0 |
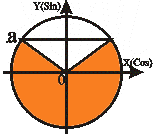 t1 = arcsin a
t2 = - П - arcsin a
t2 < t < t1
-П- arcsin a<t<arcsin a t1 = arcsin a
t2 = - П - arcsin a
t2 < t < t1
-П- arcsin a<t<arcsin a
| 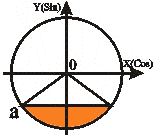 t1 = - arcsin a
t2 = - П + arcsin a
t2 < t < t1
-П+arcsin a<t<-arcsina t1 = - arcsin a
t2 = - П + arcsin a
t2 < t < t1
-П+arcsin a<t<-arcsina
|
| Учитывая, что arcSsin(-|a|) = - arcsin |a| и периодичность функции получаем для любого |a|≤1 рещение: - П -arcsin a + 2 П n < t < arcsin a + 2 П n, n Î Z. | |
| Неравенства вида sin t ≥ a | |
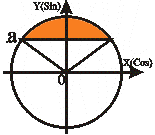 t1 = arcsin a
t2 = П - arcsin a
t1 ≤ t ≤ t2 t1 = arcsin a
t2 = П - arcsin a
t1 ≤ t ≤ t2
| 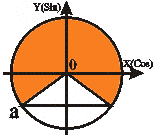 t1 = - arcsin a
t2 = П + arcsin a
t1 ≤ t ≤ t2 t1 = - arcsin a
t2 = П + arcsin a
t1 ≤ t ≤ t2
|
| Аналогично объединяем два решения: arcsin a + 2 П n ≤ t ≤ П - arcsin a +2 П n, n Î Z. | |
Решение неравенств с косинусами
| Неравенства вида cos t ≤ a | |||||||||||||||||
| 0<a<1 | -1<a<0 | ||||||||||||||||
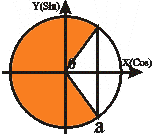 t1 = arccos a
t2 = 2П - arccos a
t1 ≤ t ≤ t2
arccosa≤t≤2П-arccosa t1 = arccos a
t2 = 2П - arccos a
t1 ≤ t ≤ t2
arccosa≤t≤2П-arccosa
| 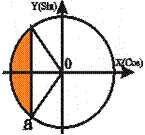 t1 = П - arccos a
t2 = П + arccos a
t1 ≤ t ≤ t2
П-arccosa≤t≤П+arccosa t1 = П - arccos a
t2 = П + arccos a
t1 ≤ t ≤ t2
П-arccosa≤t≤П+arccosa
| ||||||||||||||||
| Учитывая, что arccos(-|a|) = П - arccos |a| и периодичность функции получаем для любого |a|≤1 рещение: arccos a + 2 П n ≤ t ≤ 2 П - arccos a + 2 П n, n Î Z. | |||||||||||||||||
| Неравенства вида cos t > a | |||||||||||||||||
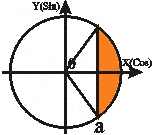 t1 = arccos a
t2 = - arccos a
t2 < t < t1 t1 = arccos a
t2 = - arccos a
t2 < t < t1
| 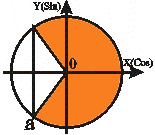 t1 = П - arccos a
t2 = - П + arccos a
t2 < t < t1 t1 = П - arccos a
t2 = - П + arccos a
t2 < t < t1
| ||||||||||||||||
| Аналогично объединяем два решения: - arccos a + 2 П n < t < П - arccos a +2 П n, n Î Z | |||||||||||||||||
| |||||||||||||||||
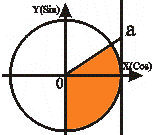
Пример 1:Решить тригонометрическое неравенство:
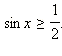
Решение
Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит Для x Î [0; 2π] решением данного неравенства будут Ответ. |
Задание 1: Решить тригонометрическое неравенство:
1. 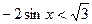
2. 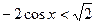
Проверь себя!
| 1. Найти значение выражения |
| 1). arccos 1+arcsin 0 |
2).arccos(-  )-arcsin )-arcsin 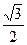
|
3). tg(arctg 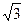 ) )
|
4). sin(arccos 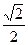 ) )
|
| 2. Решить уравнение: |
| 1). sin3xcosx-sinxcos3x=1 |
| 2). 2cos2x-5cosx=3 |
| 3). tgx-3ctgx=0 |
| 4). sin3x-sinx=0 |
| 5).2sinx+sin2x=0 |

Подготовка к Единому Государственному экзамену (ЕГЭ)
Прототипы задания В3
Основная идея решения любого тригонометрического уравнения за-
|

|

Тренировочная работа №1









 t1 = arctg a
t2 = - П/2
t2 < t < t1
-
t1 = arctg a
t2 = - П/2
t2 < t < t1
-  < t < arctg a
< t < arctg a
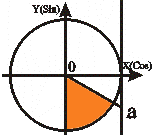 t1 = - arctg a
t2 = - П/2
t2 < t < t1
-
t1 = - arctg a
t2 = - П/2
t2 < t < t1
- 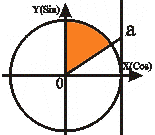 t1 = arctg a
t2 =
t1 = arctg a
t2 = 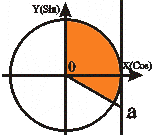 t1 = - arctg a
t2 =
t1 = - arctg a
t2 = 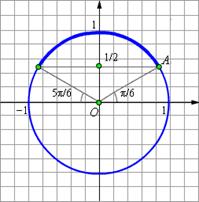 1
1
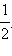
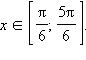 Ясно также, что если некоторое число x будет отличаться от какого-нибудь числа из указанного интервала на 2πn,
Ясно также, что если некоторое число x будет отличаться от какого-нибудь числа из указанного интервала на 2πn, 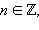 то sin x также будет не меньше
то sin x также будет не меньше 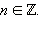 Окончательно, получаем, что решениями исходного неравенства будут все
Окончательно, получаем, что решениями исходного неравенства будут все 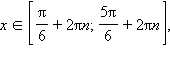 где
где