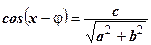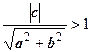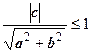Тема 8. Решение однородных относительно sinx и cosx тригонометрических уравнений
| Однородные тригонометрические уравнения и уравнения, сводящиеся к ним
| 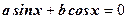
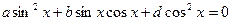 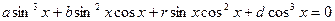
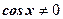 (?) Делим обе части уравнения на (?) Делим обе части уравнения на 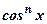
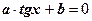 , , 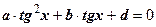 , , 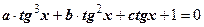 Затем применяем метод введения новой переменной.
Затем применяем метод введения новой переменной.
|
Уравнение 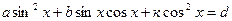 , не является однородным. Но , не является однородным. Но
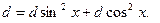
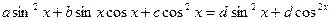
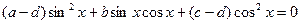 А это уже однородное тригонометрическое уравнение.
А это уже однородное тригонометрическое уравнение.
| |
Если 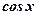 (или (или 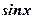 ) входит множителем во все члены уравнения, то уравнение можно решать методом разложения левой части на множители, если в правой нуль. ) входит множителем во все члены уравнения, то уравнение можно решать методом разложения левой части на множители, если в правой нуль.
|
и уравнений, приводимых к ним


Уравнение вида asinx + bcosx = c , a 2 + b 2≠0
| 1)
А это уже однородное тригонометрическое уравнение второй степени относительно | |
| 2) а)
б) ОДЗ уравнения б) уже, чем ОДЗ уравнения а). Поэтому необходимо проверять, не являются ли числа | |
| 3)
Тогда
| |
| Решений нет | 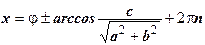 , , 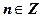 . Если . Если 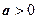 , , 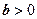 , то , то
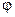 находится из условия находится из условия 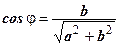 или или 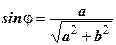 Если
Если 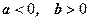 , то , то 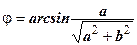 Если
Если 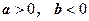 , то , то 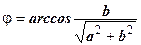
|
Задание 4: Решить тригонометрическое уравнение:
1. 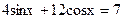 ;
;
2. 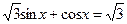 ;
;
3. 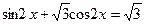
Тема 9. Решение тригонометрических уравнений
методом группировки и разложения на множители
Пример1 : Решить тригонометрическое уравнение
2 sin x cos 2x – 1 + sin x – 2cos 2x = 0
Решение:
Способом группировки разложим левую часть исходного уравнения на множители:
2 cos 2x (sin x – 1) + (sin x –1) = (sin x – 1)(2 cos 2x + 1).
Уравнение (sin x – 1)(2 cos 2x + 1) = 0 равносильно совокупности уравнений (sin x – 1) = 0,
2 cos 2x+ 1 = 0.
a) sin x – 1 = 0, sin x = 1, x =  + 2 Пn, n Î Z;
+ 2 Пn, n Î Z;
б) 2 cos 2x + 1 = 0, cos 2x = -  , 2x = ±
, 2x = ± 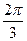 + 2Пn, nÎ Z, x = ±
+ 2Пn, nÎ Z, x = ± 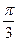 + Пn, nÎ Z
+ Пn, nÎ Z
Ответ : x =  + 2Пn, nÎ Z, x = ±
+ 2Пn, nÎ Z, x = ± 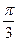 + Пn, nÎ Z
+ Пn, nÎ Z
Пример 2: Решить тригонометрическое уравнение: sin x + cos x = 1 .
Решение: Перенесём все члены уравнения влево:
sin x + cos x – 1 = 0 ,
преобразуем и разложим на множители выражение в левой части уравнения:
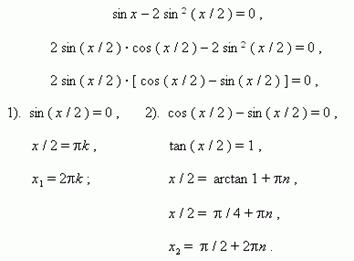
Пример 3: Решить тригонометрическое уравнение: cos 2 x + sin x · cos x = 1.
Решение : cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,
sin x · cos x – sin 2 x = 0 ,
sin x · ( cos x – sin x ) = 0 ,
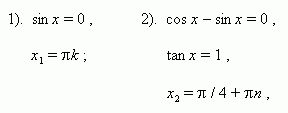
Пример 4: Решить тригонометрическое уравнение:
cos 2x – cos 8x + cos 6x = 1.
Решение : cos 2x + cos 6x = 1 + cos 8x ,
2 cos 4x cos 2x = 2 cos ² 4x ,
cos 4x · ( cos 2x – cos 4x ) = 0 ,
cos 4x · 2 sin 3x · sin x = 0 ,
1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,
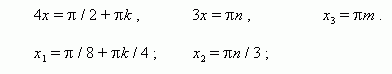
Задание 1: Решить тригонометрическое уравнение:
1. sin x – sin 2x = 0
2. 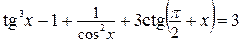
3. 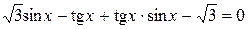
4. 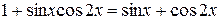
Тема 10. Решение тригонометрических уравнений,
решаемые с помощью формул сложения, понижения степени и другим
Пример 1: Решить уравнение: 2 sin x · sin 3x = cos 4x.
Решение: Преобразуем левую часть в сумму:
cos 4x – cos 8x = cos 4x ,
cos 8x = 0 ,
8x =  + πk , kÎZ
+ πk , kÎZ
x = 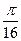 +
+ 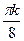 , kÎZ
, kÎZ
Ответ: x = 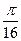 +
+ 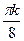 , kÎZ
, kÎZ
Задание 1: Закончить решение:
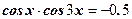
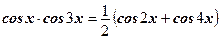
по формуле 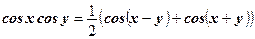
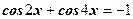
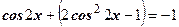
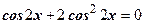
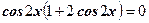
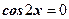 или
или 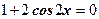
……………………………………………..
Задание 2: Решить тригонометрическое уравнение:
1. 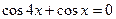
2. 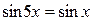
3. 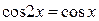
4. 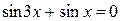









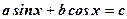
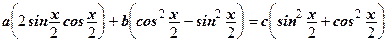
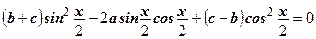
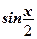 и
и 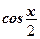 .
. 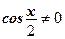 (?) Делим на
(?) Делим на 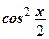
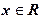
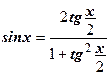
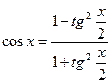
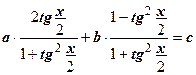 ОДЗ:
ОДЗ: 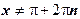
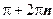 ,
, 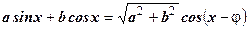 , где
, где 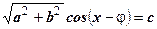 ,
,