Тема 3. Арктангенс числа, арккотангенс числа
Определение: Арктангенсом числа а℮(-  ;
;  ), называется такое число α, тангенс которого равен а.
), называется такое число α, тангенс которого равен а.
Обозначение: arctga , -  < arctga <
< arctga < 
Определение: arctga = α ↔ tgα = а
Свойства: 1) tg(arctga)=а
| а | 0 | 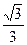 ( ( 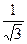 ) )
| 1 | 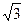
|
| arctga | 0 | 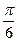
| 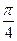
| 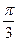
|
2) arctg(tgα)=α
Таблица значений arctga
3) arctg(-a)=- arctga
| а | - 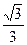 (- (- 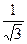 ) )
| -1 | - 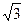
|
| arctga | - 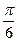
| - 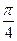
| - 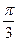
|
Пример: Вычислить:


Тема 4. Уравнение sin х = а
Определение: Тригонометрическим уравнением называется такое уравнение, в котором неизвестное содержится под знаком тригонометрической функции.
Замечание: Поскольку каждому значению тригонометрической функции соответствует неограниченное множество углов, то тригонометрическое уравнение, если не сделано каких-либо оговорок, имеет бесчисленное множество решений.
Правило: Самый общий метод решения тригонометрических уравнений состоит в том, что различные тригонометрические функции, входящие в уравнение, выражают через какую-нибудь одну из них и, принимая функцию за неизвестное, решают полученное алгебраическое уравнение, в результате чего приходят к одному из так называемых простейших тригонометрических уравнений вида:
sin x = a , cos x = b , tg x = c , ctg x = d
Общая формула корней уравнения sin x = a

х = (-1)n arcsin a +П n, n Î Z
Частные случаи
| sin x = 0 | х = Пn, n Î Z |
| sin x = 1 | х =  + 2 Пn, n Î Z + 2 Пn, n Î Z
|
| sin x = -1 | х = -  + 2Пn, n Î Z + 2Пn, n Î Z
|




Тема 5. Уравнение cos х = a
Общая формула корней уравнения cos x = a

х = ± arccos a + 2П n, n Î Z
Частные случаи
| cos x = 0 | x=  + Пn, n Î Z + Пn, n Î Z
|
| cos x = 1 | х = 2Пn, n Î Z |
| cos x = -1 | х = П + 2 Пn, n Î Z |

Тема 6. Уравнение cos х = a , tg х = а, ctg х = а
Общая формула корней уравнения tg x = a

х = arctg a + П n, n Î Z

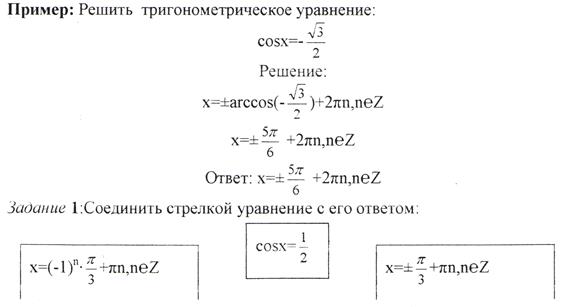
Задание 2:Решить тригонометрическое уравнение:
|
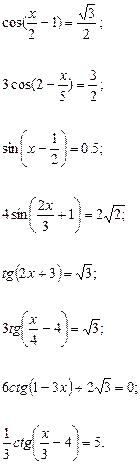
Тема 7. Решение тригонометрических уравнений,
приводимых к квадратным
Общая формула корней уравнения sin x = a

х = (-1)n arcsin a +П n, n Î Z
Общая формула корней уравнения cos x = a

х = ± arccos a + 2П n, n Î Z
Общая формула корней уравнения tg x = a

х = arctg a + П n, n Î Z


Пример: Закончить решение тригонометрического уравнения
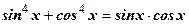
Решение:
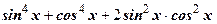
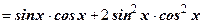
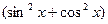 2
2 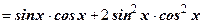
1 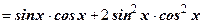
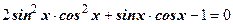
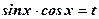
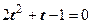
…


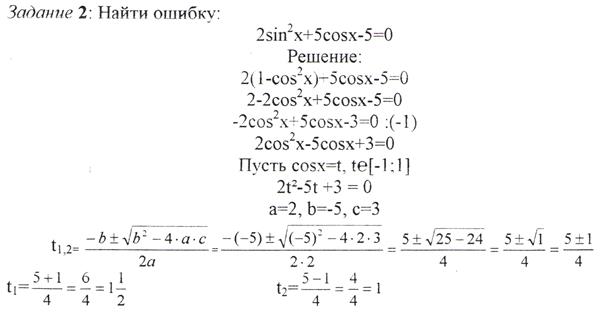
 Задание 4: Решить тригонометрическое уравнение:
Задание 4: Решить тригонометрическое уравнение:
1. 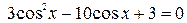 ; 6.
; 6. 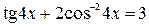 ;
;
2. 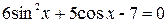 ; 7.
; 7. 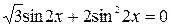 ;
;
3. 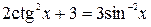 ; 8.
; 8. 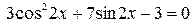 ;
;
4. 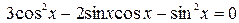 ; 9.
; 9. 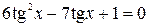 ;
;
5. 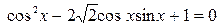 ; 10.
; 10. 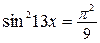 .
.








