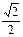Тема 1. Арксинус числа
Определение: Арксинусом числа а℮[-1;1] называется такое число α℮[-  ;
;  ], синус которого равен а.
], синус которого равен а.
Обозначение: arcsina , -  ≤ arcsina ≤
≤ arcsina ≤ 
Определение: arcsina = α ↔ sinα = а
Свойства: 1) sin(arcsina)=а
| а | 0 | 
| 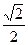 ( ( 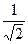 ) )
| 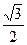
| 1 |
| arcsina | 0 | 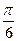
| 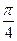
| 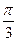
| 
|
2) arcsin(sinα)=α
Таблица значений arcsina
3) arcsin(-a)=- arcsina
| а | - 
| - 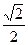
| - 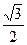
| -1 |
| arcsina | - 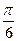
| - 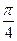
| - 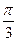
| - 
|
Пример: Вычислить:
· аrcsin1-arcsin(-1)+ arcsin(  )+arcsin(-
)+arcsin(- 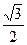 ) =
) =  -(-
-(-  )+
)+ 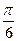 +(-
+(- 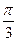 )=
)=
=  +
+  +
+ 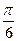 -
- 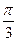 =
=  (3+
(3+  (3+
(3+ 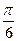 (1-
(1- 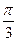 (2=
(2= 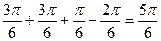
Задание 1: Закончить решение:
1) arcsin1+ arcsin 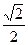 =
=  +
+ 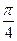 =
=  (2+
(2+ 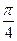 (1=
(1= 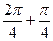 =…..
=…..
2) 4 arcsin(- 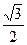 )-2 arcsin0=4∙(-
)-2 arcsin0=4∙(- 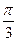 )-2∙0=…..
)-2∙0=…..
3) 3 arcsin 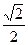 -2 arcsin(-1)=3∙
-2 arcsin(-1)=3∙ 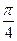 -2∙(-
-2∙(-  )=
)= 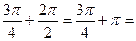 …..
…..
4) arcsin  - arcsin(-
- arcsin(-  )=
)= 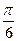 -(…..)=…..
-(…..)=…..
Задание 2: Вычислить:
1) 2 arcsin 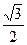 +3 arcsin (-
+3 arcsin (-  )
)
2) arcsin 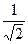 -4 arcsin1
-4 arcsin1
3) 5 arcsin(-  )+ arcsin(-1)
)+ arcsin(-1)
4) arcsin0+ arcsin(-1)+ arcsin(-  )+ arcsin(-
)+ arcsin(- 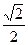 )+arcsin
)+arcsin 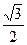
Задание 3: Выполнить по аналогии:
| 1) | sin(arcsin 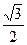 )=sin )=sin 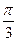 = = 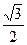
| 1) | sin(arcsin 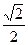 )= )=
|
| 2) | tg(2 arcsin  )=tg(2∙ )=tg(2∙ 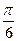 )=tg )=tg 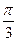 = = 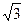
| 2) | tg(4 arcsin 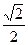 )= )=
|
| 3) | аrcsin(sin 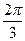 )=[свойство3 arcsin(sinα)=α]=
= )=[свойство3 arcsin(sinα)=α]=
= 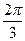
| 3) | аrcsin(2sin 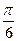 )= )=
|
| 4) | cos(аrcsin(tg 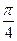 ))= cos(аrcsin1)=
= cos ))= cos(аrcsin1)=
= cos  =0 =0
| 4) | ctg(аrcsin(cos 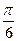 ))= ))=
|
Задание 5: Найти ошибку:
· аrcsin(cos(аrcsin(  tg(
tg( 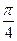 )))=аrcsin(cos(аrcsin(
)))=аrcsin(cos(аrcsin(  ∙1))= аrcsin(cos(аrcsin
∙1))= аrcsin(cos(аrcsin  ))=
))=
= аrcsin(cos 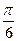 )= аrcsin
)= аrcsin  =
= 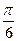
Задание 6: «Математическая цепочка»:
аrcsin  =….
=….
 |  | ||
 cos…. =…..
cos…. =…..


 аrcsin(….) = ….
аrcsin(….) = ….


 ctg… =….
ctg… =….
 |
аrcsin(- .….) =………

Тема 2. Арккосинус числа
Определение:Арккосинусом числа а℮[-1;1] называется такое число α℮[0;π], косинус которого равен а.
Обозначение: arccosa , 0≤ arccosa ≤ π
Определение: arccosa = α ↔ cosα = а
Свойства: 1) cos(arccosa)=а
| а | 0 | 
| 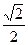 ( ( 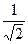 ) )
| 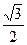
| 1 |
| arccosa | 
| 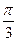
| 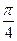
| 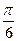
| 0 |
2) arccos(cosα)=α
Таблица значений arccosa
3) arccos(-a)=π- arccosa
| а | - 
| - 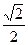
| - 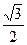
| -1 |
| arccosa | 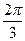
| 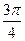
| 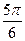
| π |
Пример: Вычислить:
· 2аrccos0+3arccos1=2∙  +3∙0=
+3∙0= 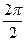 +0=π
+0=π
· 12аrccos 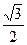 -3arccos(-
-3arccos(-  )=12∙
)=12∙ 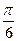 -3∙
-3∙ 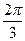 =2π-2π=0
=2π-2π=0
Задание 1: Вычислить:
1) 4аrccos(- 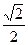 )+6arccos(-
)+6arccos(- 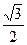 )
)
2) 5аrccos1-3arccos(-  )
)
3) 2аrccos 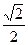 -5arccos(-1)
-5arccos(-1)
Задание 2: Соединить стрелками те функции, которые имеют одинаковое значение: 
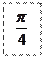 | ||||
| ||||
|
|
|
|
|
|
|
|
Задание 3:Выполнить:
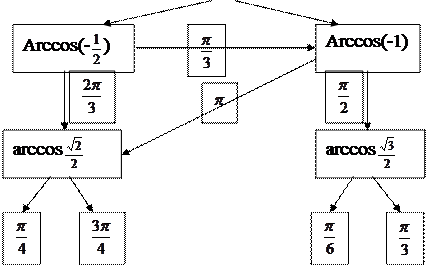 |
Задание 4: Найти ошибку:
· аrccos (- 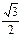 )+3аrcsin(-1)=
)+3аrcsin(-1)= 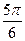 +3∙π=
+3∙π= 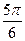 +
+ 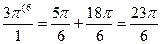
Задание 5: Закончить решение:
1) 4arcsin(-  )+ arcos(-
)+ arcos(- 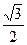 )=4∙(-
)=4∙(- 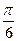 )+
)+ 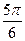 =-
=- 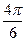 +
+ 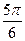 =….
=….
2) arccos 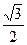 +4 arccos
+4 arccos  -arcsin
-arcsin  =
= 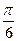 +4∙
+4∙ 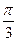 -
- 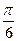 =….
=….
3) arcsin 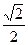 +4 arcsin(-
+4 arcsin(- 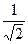 )-arcсos
)-arcсos 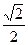 =
= 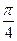 +4∙(-….)-…..=…..
+4∙(-….)-…..=…..
Задание 6: Вычислить:
1) arcsin 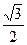 +arccos (-
+arccos (-  )
)
2) arcsin(- 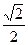 )+6 arccos1
)+6 arccos1
3) 3arcsin0+ 5arccos(-1)+ arcsin(-  )+ arccos(-
)+ arccos(- 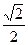 )+3arccos
)+3arccos 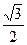
Задание 7: Выполнить по аналогии:
| 1) | cos(arccos 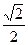 )=sin )=sin 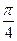 = = 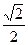
| 1) | cos(arccos  )= )=
|
| 2) | sin(arccos 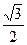 )=sin( )=sin( 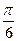 )= )= 
| 2) | tg(arccos 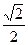 )= )=
|
| 3) | Cos(2arccos 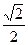 )=cos(2∙ )=cos(2∙ 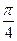 )=
=cos )=
=cos  =0 =0
| 3) | cos(3аrccos  )= )=
|
| 4) | sin(6аrccos  )= sin(6∙ )= sin(6∙ 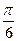 )=
= sinπ=0 )=
= sinπ=0
| 4) | tg(2аrccos 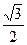 )= )=
|