Тема «тригонометрические уравнения и неравенства»
Государственное автономное профессиональное образовательное учреждение
Свердловской области
«Каменск-Уральский техникум торговли и сервиса»
 |
Учебно-методический комплекс
по алгебре и началам анализа
Тема «ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
Структура рабочей тетради соответствует структуре учебного пособия; уровень заданий соответствует требованиям, предъявляемым федеральной программой к уровню математической подготовки обучающихся; система заданий дополняет и расширяет систему заданий учебника.
Данная рабочая тетрадь разработана с учётом того, что в рабочей программе дисциплины «математика» на тему «Тригонометрические уравнения и неравенства » отводится 20-26 часов.
Рабочая тетрадь содержит основные понятия теории и основные формулы, а также набор заданий для самостоятельной работы. Обязательно включено решение одной, двух типовых задач по каждой теме. В заключении предложено выполнить несколько тренировочных тестов по форме ЕГЭ .
Основная задача учебно-методического комплекса – способствовать формированию у студентов прочных знаний по теме «Тригонометрические уравнения и неравенства», в частности при вычислении выражений, содержащих arcsina, arccosa, arctga, а также при решении тригонометрических уравнений различной сложности.
Разработчик: Решетникова Яна Евгеньевна, ГАПОУ СО «Каменск-Уральский техникум торговли и сервиса»
Введение
Данная рабочая тетрадь может использоваться как самостоятельно (так как в тетрадь включены не только множество заданий разной степени сложности, но и все необходимые определения, подробные примеры и пояснения к ним), так и совместно с учебниками:
§ «Алгебра и начала анализа 10-11 класс» Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Шабунин М.И., М:Просвещение;
§ «Алгебра и начала анализа 10класс» Колягин Ю.М., Сидоров Ю.В., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И., М:Мнемозина;
Структура рабочей тетради соответствует структуре учебного пособия; уровень заданий соответствует требованиям, предъявляемым федеральной программой к уровню математической подготовки обучающихся; система заданий дополняет и расширяет систему заданий учебника. Рабочая тетрадь содержит основные понятия теории и основные формулы, а также набор заданий для самостоятельной работы. Обязательно включено решение одной, двух типовых задач по каждой теме. В заключении предложено выполнить несколько тренировочных тестов по форме ЕГЭ .
В данной рабочей тетради использованы различные формы изложения материала. Для изучения нового материала рабочие тетради оформлены как полноценный конспект, в котором есть и теория, и примеры решённых заданий, и задания для самостоятельного выполнения. Учебные пособия - рабочие тетради, разработаны так, что по алгоритму и количественной части решённого, а также с учетом возрастания сложности необходимо выполнить задание. При выполнении данных заданий требуются умения систематизировать, сравнивать, анализировать предложенную информацию, применять имеющиеся знания и умения в нестандартной ситуации. Причём информация представлена в различных видах (схемы, таблицы и тд.). Задание так же имеют разную формулировку и различны по своему характеру: вводные, пробные, по образцу, творческие. Помимо упражнений и заданий в тетради включены и справочные материалы. В конце тетради предлагается уровневая контрольная работа, но выполнять её можно частями (при окончании изучения тем «Arcsina», «Arccosa», «Arctga», «Arcctga», «Решение тригонометрических уравнений» и «Решение тригонометрических неравенств»), чтобы легче контролировать усвоение материала и корректировать ошибки.
Использование рабочей тетради в учебном процессе позволяет осуществить: во-первых, достижение уровня обязательной математической подготовки; во-вторых сформировать умение применять полученные знания в несколько отличных от обязательных результатов обучения ситуациях; в – третьих ведёт к повышению активности и самостоятельности, планированию собственной деятельности.
Содержание учебного материала
| Раздел Тригонометрические уравнения | |
| Тема 1 Арксинус числа | Определение арксинуса |
| Тема 2 Арккосинус числа | Определение арккосинуса |
| Тема 3 Арктангенс числа, арккотангенс числа. | Определение арксинуса, арккосинуса, арктангенса. |
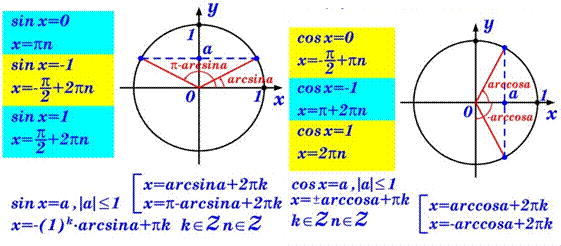
| Тема 4 Уравнение sin х = а | Формулы корней, особую форму записи решений для частных случаев |
| Тема 5 Уравнение cos х = а Уравнения tg х = а, ctg х = а | Формулы корней, особую форму записи решений для частных случаев |
| Тема 6 Уравнения tg х = а, ctg х = а | Формулы корней, особую форму записи решений для частных случаев |
| Тема 7 Решение тригонометрических уравнений, приводимых к квадратным | Основные тригонометрические формулы, формулы для решения простейших тригонометрических уравнений |
| Тема 8 Решение однородных тригонометрических уравнений и уравнений, приводимых к ним | Основные формулы для решения уравнений |
| Тема 9 Решение тригонометрических уравнений методом группировки и разложения на множители | Способы решения уравнений методом группировки и разложением на множители. |
| Тема 10 Решение тригонометрических уравнений, решаемые с помощью формул сложения, понижения степени и другим | Основные формулы для решения уравнений |
| Тема 11 Решение простейших тригонометрических неравенств | Определение простейших тригонометрических неравенств, различные способы их решения |
Историческая справка
Слово “тригонометрия” впервые встречается в 1505 году в заглавии книги немецкого математика Питискуса. Слово это греческого происхождения и в переводе означает “Наука об измерении треугольника”. Поэтому впервые с понятиями “синус” и “косинус” учащиеся встречаются при изучении темы “Прямоугольный треугольник”.
Самую длительную историю имеет синус. Его знали ещё Евклид и Архимед. Синус - это изгиб, кривизна. Понятие “косинус” моложе, и означало дополнительный синус. Тангенс появился тогда, когда возникла необходимость решать задачи с помощью длины тени. Тангенс означает касающийся. Понятия “тангенс”, “арктангенс”, “секанс”, “косеканс” введены арабскими математиками в X веке. Современные обозначения arcsin и arccos появились в 1772 году.
Современный вид тригонометрии придал великий математик XVIII века - Леонардо Эйлер. Именно Эйлер ввёл определение тригонометрических функций, получил формулы приведения. А термин “функция” ввёл в 1673 году Г. Лейбниц.
В 19 в. дальнейшее развитие теории тригонометрических функций было продолжено в работах русского математика Н.Л.Лобачевского (1792-1856), а также в трудах других ученых, например в работах профессоров МГУ Д.Е. Меньшова и Н.К. Бари.
Ещё древнегреческие математики, используя элементы тригонометрии для решения прямоугольных треугольников, фактически составляли и решали простейшие тригонометрические уравнения типа: sin x = a, где 0 < x < П/2 и |a| < 1.
Исторически учение о решении тригонометрических уравнений формировалось с развитием теории тригонометрических функций, а также черпало из алгебры общие методы их решения. Часть тригонометрических уравнений непосредственно решается сведением их к простейшему виду, иногда – с предварительным разложением левой части уравнения на множители, когда правая часть равна 0. В некоторых случаях удается произвести замену неизвестных таким образом, что тригонометрическое уравнение преобразуется в «удобное» для решения алгебраическое уравнение.
К сожалению, нельзя указать общего метода решения тригонометрических уравнений, почти каждое из них (кроме простейших) требует особого подхода.
Решение тригонометрических неравенств стоит в одном ряду с такими важными темами, как решение числовых неравенств и решение систем неравенств с одной переменной. Исторически сложилось, что тригонометрическим уравнениям и неравенствам уделялось особое место в школьном курсе. Еще греки, на заре человечества, считали тригонометрию важнейшей из наук, ибо геометрия - царица математики, а тригонометрия - царица геометрии. Поэтому и мы, не оспаривая древних греков, будем считать тригонометрию одним из важнейших разделов школьного курса, да и всей математической науки в целом.